江苏省镇江市八校2021届高三上学期期中联考数学试题（word版含答案） 9页

江苏省镇江市八校2021届高三上学期期中联考 数学试题 ‎2020．11‎ 一、单项选择题（本大题共8小题，每小题5分，共计40分．在每小题给出的四个选项中，只有一个是符合题目要求的，请把答案添涂在答题卡相应位置上）‎ ‎1．已知A＝，B＝，则AB＝‎ ‎ A．[，) B．(0，)‎ C．(0，) D．(，0)[，)‎ ‎2．已知（i为虚数单位，aR），则a＝‎ ‎ A．﹣2 B．﹣1 C．1 D．2‎ ‎3．甲、乙两人进行羽毛球比赛，比赛采取五局三胜制，无论哪方先胜三局比赛都结束，假定甲每局比赛获胜的概率均为，则甲以3：1的比分获胜的概率为 ‎ A． B． C． D．‎ ‎4．“sin2＝”是“tan＝2”的 A．充分不必要条件 B．必要不充分条件 ‎ C．充要条件 D．既不充分也不必要条件 ‎5．已知二面角—l—，其中平面的一个法向量＝(1，0，﹣1)，平面的一个法向量＝(0，﹣1，1)，则二面角—l—的大小可能为 ‎ A．60° B．120° C．60°或120° D．30°‎ ‎6．曲线在点(1，0)处的切线方程是 ‎ A． B． C． D．‎ ‎7．意大利数学家斐波那契以兔子繁殖为例，引入“兔子数列”：1，1，2，3，5，8，13，21，34，55， …即，(n≥3，n)，此数列在现代物理、化学等方面都有着广泛的应用，若此数列的每一项被2除后的余数构成一个新数列，则数列的前2020项的和为 ‎ A．1348 B．1358 C．1347 D．1357‎ ‎8．已知等差数列的前n项和为，公差d＞0，和是函数 ‎ 9‎ 的极值点，则＝‎ ‎ A．﹣38 B．38 C．﹣17 D．17‎ 二、 多项选择题（本大题共4小题，每小题5分， 共计20分．在每小题给出的四个选项中，至少有两个是符合题目要求的，请把答案添涂在答题卡相应位置上）‎ ‎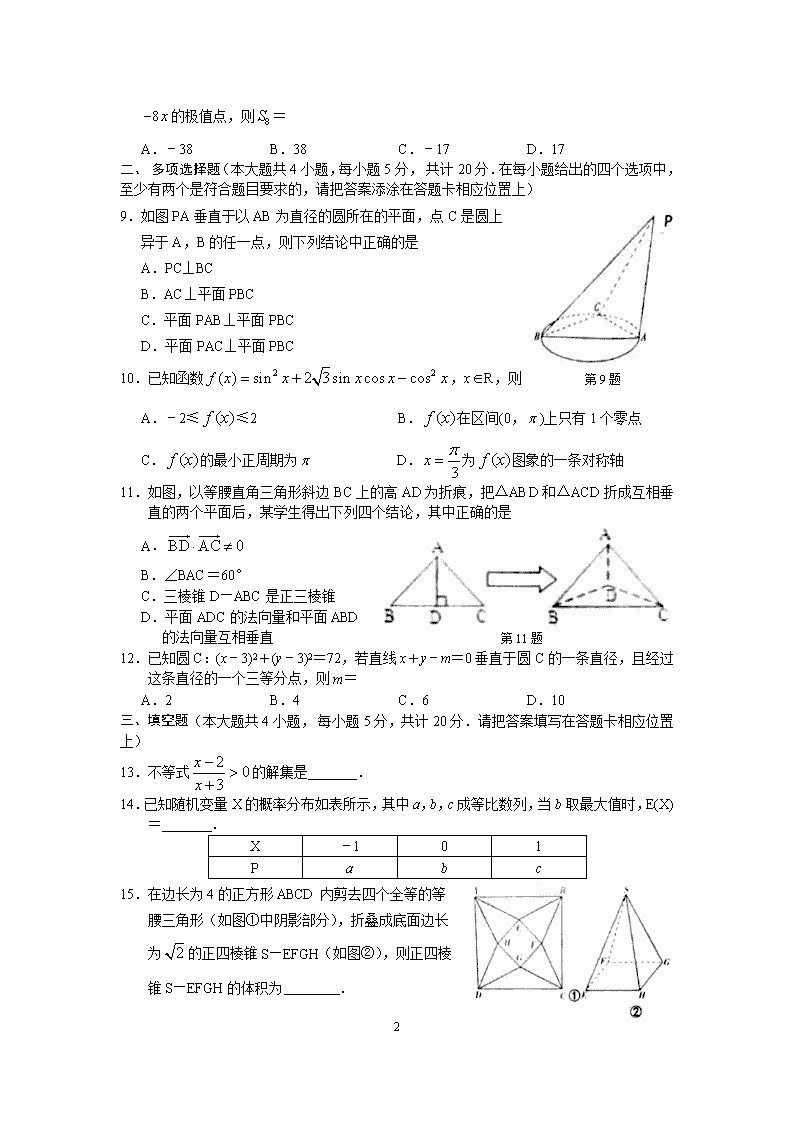9．如图PA垂直于以AB为直径的圆所在的平面，点C是圆上 异于A，B的任一点，则下列结论中正确的是 A．PC⊥BC B．AC⊥平面PBC C．平面PAB⊥平面PBC D．平面PAC⊥平面PBC ‎10．已知函数，xR，则 第9题 A．﹣2≤≤2 B．在区间(0，)上只有1个零点 C．的最小正周期为 D．为图象的一条对称轴 ‎11．如图，以等腰直角三角形斜边BC上的高AD为折痕，把△ABD和△ACD折成互相垂直的两个平面后，某学生得出下列四个结论，其中正确的是 A．‎ B．∠BAC＝60°‎ C．三棱锥D—ABC是正三棱锥 D．平面ADC的法向量和平面ABD 的法向量互相垂直 第11题 ‎12．已知圆C：(x﹣3)2＋(y﹣3)2＝72，若直线x＋y﹣m＝0垂直于圆C的一条直径，且经过这条直径的一个三等分点，则m＝‎ A．2 B．4 C．6 D．10‎ 三、填空题（本大题共4小题， 每小题5分，共计20分．请把答案填写在答题卡相应位置上）‎ ‎13．不等式的解集是 ．‎ ‎14．已知随机变量X的概率分布如表所示，其中a，b，c成等比数列，当b取最大值时，E(X)＝ ．‎ X ‎﹣1‎ ‎0‎ ‎1‎ P a b c ‎15．在边长为4的正方形ABCD内剪去四个全等的等 腰三角形（如图①中阴影部分），折叠成底面边长 为的正四棱锥S—EFGH（如图②），则正四棱 锥S—EFGH的体积为 ．‎ ‎ 第15题 9‎ ‎16．数列的前n项和为，定义的“优值”为，现已知的“优值”，则 ， ．‎ 四、解答题（本大题共6小题，共计70分．请在答题卡指定区域内作答．解答时应写出文字说明、证明过程或演算步骤）‎ ‎17．（本小题满分10分）‎ 设函数，正项数列满足，，n，且n≥2．‎ ‎（1）求数列的通项公式；‎ ‎（2）求证：．‎ ‎18．（本小题满分12分）‎ 在①sinBsinC＝；②tanB＋tanC＝这两个条件中任选一个，补充到下面问题中，并进行作答．‎ 在△ABC中，内角A，B，C的对边分别为a，b，c，tanBtanC＝，a＝， ．‎ ‎（1）求角A，B，C的大小；‎ ‎（2）求△ABC的周长和面积．‎ ‎19．（本小题满分12分）‎ 在直角坐标系xOy中，以坐标原点O为圆心的圆与直线相切．‎ ‎（1）求圆O的方程；‎ ‎（2）若圆O上有两点M，N关于直线x＋2y＝0对称，且，求直线MN的方程．‎ 9‎ ‎20．（本小题满分12分）‎ 如图，在四棱锥P—ABCD中，底面ABCD是菱形，∠DAB＝60°，PD⊥平面ABCD，PD＝AD＝1，点E，F分别为AB和PD的中点．‎ ‎（1）求证：直线AF∥平面PEC；‎ ‎（2）求PC与平面PAB所成角的正弦值．‎ ‎21．（本小题满分12分）‎ 偏差是指个别测定值与测定的平均值之差，在成绩统计中，我们把某个同学的某科考试成绩与该科班平均分的差叫某科偏差，在某次考试成绩统计中，某老师为了对学生数学偏差x （单位：分）与物理偏差y（单位：分）之间的关系进行分析，随机挑选了8位同学，得到他们的两科成绩偏差数据如下：‎ 学生序号 ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ ‎7‎ ‎8‎ 数学偏差x ‎20‎ ‎15‎ ‎13‎ ‎3‎ ‎2‎ ‎﹣5‎ ‎﹣10‎ ‎﹣18‎ 物理偏差y ‎6.5‎ ‎3.5‎ ‎3.5‎ ‎1.5‎ ‎0.5‎ ‎﹣0.5‎ ‎﹣2.5‎ ‎﹣3.5‎ ‎（1）若x与y之间具有线性相关关系，求y关于x的线性回归方程；‎ ‎（2）若该次考试该数学平均分为120分，物理平均分为91.5分，试由（1）的结论预测数学成绩为128分的同学的物理成绩．‎ 附参考公式：‎ ‎，．‎ ‎22．（本小题满分12分）‎ 已知函数．‎ ‎（1）当a＝1时，求函数在[1，)上的最小值；‎ ‎（2）若函数在[1，)上的最小值为1，求实数a的取值范围；‎ ‎（3）若，讨论函数在[1，)上的零点个数．‎ 9‎ 参考答案 ‎1．B 2．D 3．A 4．B 5．C 6．D 7．C 8．A ‎9．AD 10．ACD 11．BC 12．AD ‎13．(，﹣3)(2，) 14．0 15． 16．，‎ ‎17．‎ ‎18．‎ 9‎ ‎19．‎ ‎ ‎ ‎20．（1）‎ 9‎ ‎（2）‎ 9‎ ‎21．‎ ‎ ‎ ‎22．‎ 9‎ 9‎