新教材数学人教B版必修第二册教师用书（含习题测试）：6-4-3 余弦定理、正弦定理 第4课时　余弦定理、正弦定理应用举例 23页

第 4 课时 余弦定理、正弦定理应用举例 课 标 解 读 课标要求 核心素养 1.能将实际问题转化为解三角形问题.(难 点) 2.能够用正、余弦定理等知识和方法求解与 高度、角度有关的实际应用问题.(重点) 1.通过应用正、余弦定理求高度、角度问题,培 养学生的数学运算素养. 2.借助将实际问题转化为解三角形问题,培养学 生的数学建模素养. 近测高塔远看山,量天度海只等闲; 古有九章勾股法,今看三角正余弦. 为了测定河岸 A 点到对岸 C 点的距离,在岸边选定 100 米长的基线 AB,并测得 ∠ABC=60°,∠BAC=45°. 问题:已知这三个元素能求 A,C 两点之间的距离吗? 答案 能,利用正弦定理就可以. 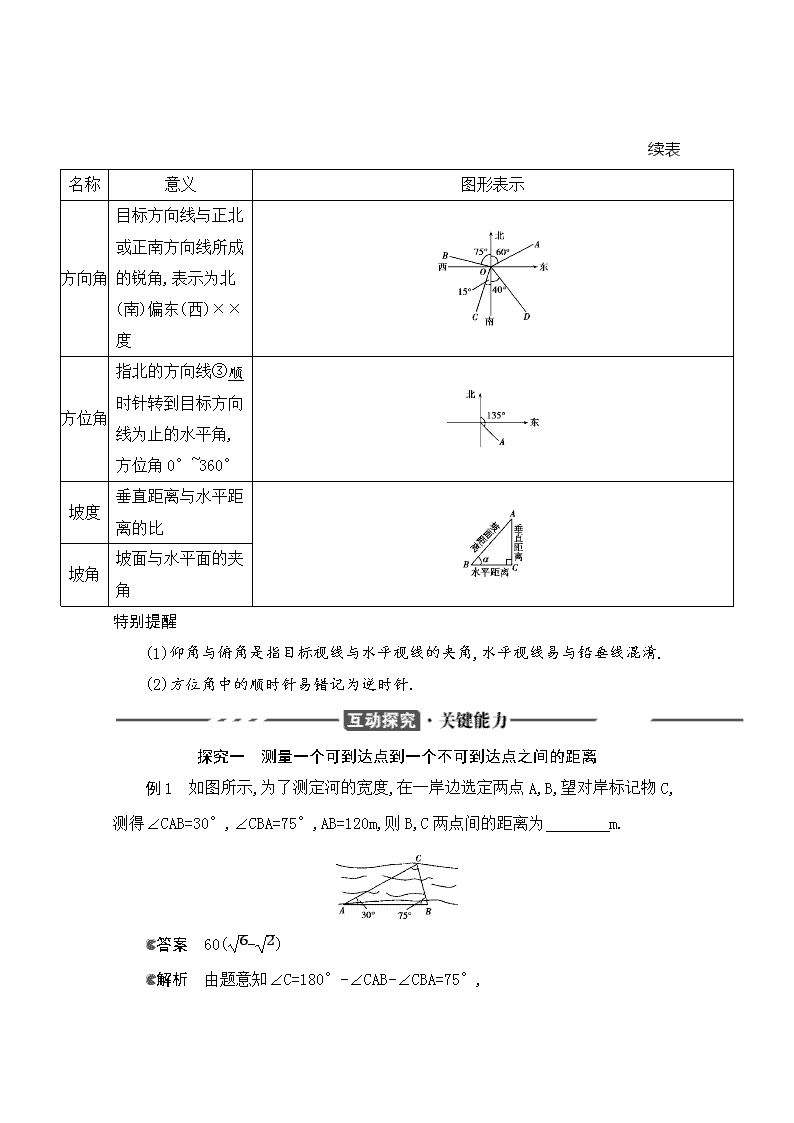实际问题中的有关术语: 名称 意义 图形表示 仰角 和 俯角 测量时,以水平线 为基准,视线在水 平线上方时与水平 线所成的角叫做① 仰角;视线在水平 线下方时与水平线 所成的角叫做②俯 角 续表 名称 意义 图形表示 方向 角 目标方向线与正北 或正南方向线所成 的锐角,表示为北 (南)偏东(西)×× 度 方位 角 指北的方向线③顺 时针转到目标方向 线为止的水平角, 方位角 0°~360° 坡度 垂直距离与水平距 离的比 坡角 坡面与水平面的夹 角 特别提醒 (1)仰角与俯角是指目标视线与水平视线的夹角,水平视线易与铅垂线混淆. (2)方位角中的顺时针易错记为逆时针. 探究一 测量一个可到达点到一个不可到达点之间的距离 例 1 如图所示,为了测定河的宽度,在一岸边选定两点 A,B,望对岸标记物 C, 测得∠CAB=30°,∠CBA=75°,AB=120m,则 B,C 两点间的距离为 m. 答案 60( 6 - 2 ) 解析 由题意知∠C=180°-∠CAB-∠CBA=75°, 由正弦定理,得 㘵 sin30 ° = sin75 ° , 而 sin75°=sin(30°+45°)=sin30°cos45°+cos30°sin45°= 6+ 2 4 , 所以 BC= · sin30 ° sin75 ° = 120 × 1 2 6+ 2 4 =60( 6 - 2 )(m). (变结论)本例条件不变,改为求河的宽度. 解析 由题意知,∠ACB=180°-30°-75°=75°, ∴△ABC 为等腰三角形. 河宽即 AB 边上的高, AB 边上的高与 AC 边上的高相等, ∴过 B 作 BD⊥AC 于 D, ∴河宽 BD=120×sin30°=60(m). 思维突破 求距离问题时的注意点 (1)选定或确定所求量所在的三角形.若其他量已知,则直接解;若有未知量, 则把未知量放在另一确定的三角形中求解. (2)确定用正弦定理还是余弦定理,如果都可用,就选择更便于计算的定理. 1-1 学校体育馆的人字屋架为等腰三角形,如图所示,测得 AC 的长度为 4m,∠A=30°,则其跨度 AB 的长为( ) A.12m B.8m C.3 3 m D.4 3 m 答案 D 由题意知,∠A=∠B=30°, 所以∠C=180°-30°-30°=120°, 由正弦定理,得 sin㘵 = 㘵 sin , 即 AB= 㘵 · sin㘵 sin = 4 × sin120 ° sin30 ° =4 3 (m). 探究二 测量两个不可到达的点之间的距离 例 2 如图,CD 是某铁路线上的一条穿山隧道,开凿前,在 CD 所在水平面上的 山体外取点 A,B,并测得四边形 ABCD 中,∠ABC= π 3 ,∠BAD= 2π 3 ,AB=BC=400 米,AD=250 米, 则应开凿的隧道 CD 的长为 米. 答案 350 解析 在△ABC 中,AB=BC=400 米,∠ABC= π 3 , 所以△ABC 为等边三角形,∠BAC= π 3 ,AC=AB=BC=400 米, 又∠BAD= 2π 3 ,所以∠CAD= π 3 , 所以在△ACD 中,由余弦定理,得 CD2=AC2+AD2-2AC·ADcos∠CAD=4002+2502-2×400×250cos π 3 =122500, 所以 CD=350 米. 思维突破 利用正、余弦定理测量不能到达的两点间的距离,是解斜三角形的一个重要方 法,关键是构造一个或几个三角形,测出有关边长和角,再用正、余弦定理进行计 算. 2-1 如图,某炮兵阵地位于 A 点,两观察所分别位于 C,D 两点.已知△ACD 为正三角 形,且 DC= 3 km,当目标出现在 B 点时,测得∠CDB=45°,∠BCD=75°,则炮兵阵地与目 标的距离约是( ) A.1.1km B.2.2km C.2.9km D.3.5km 答案 C ∠CBD=180°-∠BCD-∠CDB=60°. 在△BCD 中,由正弦定理,得 BD= 㘵sin75 ° sin60 ° = 6+ 2 2 km. 在△ABD 中,∠ADB=45°+60°=105°, 由余弦定理,得 AB2=AD2+BD2-2AD·BDcos105° =3+ ( 6+ 2)2 4 +2× 3 × 6+ 2 2 × 6- 2 4=5+2 3 . 所以 AB= 5 + 2 3 ≈2.9(km). 所以炮兵阵地与目标的距离约为 2.9km. 探究三 航行中的距离问题 例 3 如图,A,B 是海面上位于东西方向相距 5(3+ 3 )海里的两个观测点,现位 于 A 点北偏东 45°,B 点北偏西 60°的 D 点有一艘轮船发出求救信号,位于 B 点南 偏西 60°且与 B 点相距 20 3 海里的 C 点的救援船立即前往营救,其航行速度为 30 海里/小时,该救援船到达 D 点至少需要多长时间? 解析 由题意知 AB=5(3+ 3 )海里, 因为∠DAB=90°-45°=45°,∠DBA=90°-60°=30°, 所以∠ADB=180°-(45°+30°)=105°, 在△ADB 中,由正弦定理,得 sin ∠ = sin ∠ , 所以 DB= sin ∠ sin ∠ = 5(3+ 3) × sin45 ° sin105 ° = 5(3+ 3) × sin45 ° sin45 ° cos60 ° +cos45 ° sin60 ° = 5(3+ 3) × 2 2 2 4 + 6 4 = 5 3( 3+1) 3+1 2 =10 3 (海里), 又因为∠DBC=∠DBA+∠ABC=30°+(90°-60°)=60°,BC=20 3 海里, 所以在△DBC 中,由余弦定理,得 CD2=BD2+BC2-2BD·BCcos∠DBC=300+1200-2×10 3 ×20 3 × 1 2 =900, 所以 CD=30 海里(负值舍去), 所以需要的时间为 30÷30=1(小时), 即救援船到达 D 点至少需要 1 小时. (变条件、变结论)本例中若不知救援船的速度,其他条件不变,要求救援船必须 在 40 分钟内到达,则救援船的最小速度为多少?. 解析 设救援船的速度为 v 海里/小时,由本例解析求得 CD=30 海里,由 30 ≤ 40 60 ,得 v≥45. 即救援船的最小速度为 45 海里/小时. 思维突破 在航行问题中,通常是把方位角(方向角)与几何图形结合起来,一是从图形的 完整性方面画出图形;二是把多边形向三角形转化. 探究四 测量高度问题 例 4 如图,为了测量河对岸的塔高 AB,有不同的方案,其中之一是选取与塔底 B 在同一水平面内的两个测点 C 和 D,测得 CD=200 米,在 C 点和 D 点测得塔顶 A 的 仰角分别是 45°,30°,且∠CBD=30°,求塔高 AB. 解析 在 Rt△ABC 中,∠ACB=45°,设 AB=h,则 BC=h. 在 Rt△ABD 中,∠ADB=30°,则 BD= 3 h. 在△BCD 中,由余弦定理,得 CD2=BC2+BD2-2·BC·BD·cos∠CBD, 即 2002=h2+( 3 h)2-2·h· 3 h· 3 2 , 所以 h2=2002,解得 h=200(h=-200 舍去), 即塔高 AB=200 米. 思维突破 解决有关高度问题时要注意的两个问题 (1)要清楚仰角与俯角的区别与联系. (2)测量底部不能到达的建筑物的高度问题,一般是转化为直角三角形模型, 但在某些情况下,仍需根据正、余弦定理来解决. 4-1 一轮船要通过一座跨江大桥,驾驶员在 A 处测得桥拱上端 D 的仰角为 8°,轮 船向前航行 200m 后到达 B 处,又测得桥拱上端 D 的仰角为 26°,若轮船驾驶舱离水 面 20m,轮船最高处距离驾驶舱上方有 30m.问轮船能否通过这座跨江大 桥?(sin18°≈0.3090,sin154°≈0.4384,sin8°≈0.1392,精确到 0.1m) 解析 如图,∠DAB=8°,∠DBC=26°,AB=200m, 则∠ADB=18°,∠ABD=154°, ∴AD= sin18 °·sin154°≈283.8(m), DC=AD·sin8°≈39.5(m),又 39.5m>30m, ∴轮船能通过这座跨江大桥. 探究五 测量角度问题 例 5 甲船在 A 处发现乙船在北偏东 60°的 B 处,乙船正以 anmile/h 的速度 向北行驶.已知甲船的速度是 3 anmile/h,甲船应沿着 方向前进,才能最 快与乙船相遇. 答案 北偏东 30° 解析 如图,设经过 th 两船在 C 点相遇, 则在△ABC 中,BC=atnmile, AC= 3 atnmile,B=180°-60°=120°, 由 㘵 sin ∠ 㘵 = 㘵 sin ,得 sin∠CAB= 㘵sin 㘵 = · sin120 ° 3at = 1 2 . ∵0°<∠CAB<60°, ∴∠CAB=30°,∴∠DAC=60°-30°=30°. 即甲船应沿北偏东 30°的方向前进,才能最快与乙船相遇. 思维突破 测量角度问题的解题思路 (1)通过认真审题,结合已知条件画出示意图. (2)确定所求角在示意图中对应的可解三角形. (3)把已知条件中的方向角、方位角、距离等,借助平面几何和立体几何的相 关知识,转化成该三角形中的边和角(至少有一边). (4)利用正弦定理或余弦定理求解. 5-1 如图,甲船在 A 处遇险,在甲船西南 10 海里 B 处的乙船收到甲船的警报后,测 得甲船是沿着北偏西 15°的方向,以 9 海里/时的速度向某岛 C 靠近,如果乙船要在 40 分钟后追上甲船,则乙船应以多大速度,以何方向角航行? 解析 设乙船速度为 x 海里/时,且乙船在 40 分钟后的点 C 处追上甲船,则 BC= 40 60 x= 2 3 x(海里),AC= 40 60 ×9=6(海里). 由余弦定理,得 BC2=AB2+AC2-2AB·ACcos∠BAC, 即 2 3 x 2 =102+62-2×10×6×cos(90°-15°+45°), ∴x=21,BC=14. 由正弦定理,得 㘵 sin ∠ 㘵 = 㘵 sin , ∴sinB= 6 14 ×sin120°≈0.37, ∴B≈21°47'. 答:乙船应以 21 海里/时的速度沿北偏东 23°13'航行. 1.为了测某塔AB的高度,在一幢与塔AB相距20m的楼顶处测得塔顶的仰角为30°, 塔基的俯角为 45°,那么塔 AB 的高为( ) A.20 1 + 3 3 m B.20 1 + 3 2 m C.20(1+ 3 )m D.30m 答案 A 塔的高度为 20tan30°+20tan45°=20 1 + 3 3 (m). 2.如图所示,在山底 A 处测得山顶 B 的仰角∠CAB=45°,沿倾斜角为 30°的山坡向山 顶走 1000m 到达点 S,又测得山顶仰角∠DSB=75°,则山高 BC 为( ) A.500 2 m B.200m C.1000 2 m D.1000m 答案 D ∵∠CAB=45°,∠CAS=30°,∴∠SAB=45°-30°=15°, ∠SBA=∠ABC-∠SBC=45°-(90°-75°)=30°,∠ASB=180°-15°-30°=135°. 在△ABS 中, AB= · sin135 ° sin30 ° = 1000 × 2 2 1 2 =1000 2 (m), ∴BC=AB·sin45°=1000 2 × 2 2=1000(m). 3.在相距 12 千米的 A,B 两个小岛处测量目标 C 岛,测得∠CAB=75°,∠CBA=60°,则 A,C 间的距离为( ) A.2 6 千米B.6 6 千米 C.2 2 千米D.4 2 千米 答案 B ∵∠CAB=75°,∠CBA=60°, ∴∠ACB=180°-(∠CAB+∠CBA)=45°. 由正弦定理,得 㘵 sin ∠ 㘵 = sin ∠ 㘵 , ∴AC= sin45 ° ×sin60°=6 6 千米. 4.有一条与两岸平行的河流,水速为 1m/s,小船速度为 2 m/s,为使所走路程最短, 小船应朝与水速成 方向行驶. 答案 135° 解析 如图,小船从 A 处过河,则设小船行驶的方向与岸成α,则因为水速为 1m/s, 小船的速度为 2 m/s,则α=45°,小船的方向与水速成 180°-45°=135°. 5.设地平面上一旗杆为 OP,为测得它的高度 h,在地平面上取一基线 AB,AB=200m, 在 A 处测得 P 点的仰角为∠OAP=30°,在 B 处测得 P 点的仰角为∠OBP=45°,又测得 ∠AOB=60°,求旗杆的高 h. 解析 ∵OP=h,∠OAP=30°,∠OBP=45°,∠AOB=60°,AB=200m. 在△AOP 中,因为 OP⊥OA,所以∠AOP=90°, 则 OA= tan30 ° = 3 h, 同理,在△BOP 中,∠BOP=90°,且∠OBP=45°, 所以 OB=OP=h. 在△OAB 中,由余弦定理,得 AB2=OA2+OB2-2OA·OB·cos∠AOB, 即 2002=3h2+h2-2 3 h2·cos60°, 解得 h= 200 4- 3 . 答:旗杆的高 h 为 200 4- 3 m. 数学建模——根据条件选择恰当的数学模型 甲船在 A 处,乙船在 A 处的南偏东 45°方向,距 A 有 9 海里的 B 处,向正南方向 行驶,而甲船沿南偏东 15°的方向并以 28 海里/时的速度行驶,恰能与乙船相遇, 试求乙船的速度.(结果保留根号,无需求近似值) 解析 设乙船的速度为 x 海里/时,经过 t 小时甲船追上乙船,且在 C 处相遇 (如图所示), 则在△ABC 中,AC=28t,BC=xt, ∠CAB=45°-15°=30°,∠ABC=180°-45°=135°. 由正弦定理,得 㘵 sin ∠ 㘵 = 㘵 sin ∠ 㘵 , 即 28 sin135 ° = sin30 ° , 所以 x= 28 × sin30 ° sin135 ° = 28 × 1 2 2 2 =14 2 . 答:乙船的速度为每小时 14 2 海里. 素养探究:作出示意图,把已知条件转化为三角形中的已知元素,利用正弦定 理、余弦定理解决问题,过程中体现数学建模的核心素养. 某港口 O 要将一件重要物品用小艇送到一艘正在航行的轮船上,在小艇出发时, 轮船位于港口 O 北偏西 30°且与该港口相距 20 海里的 A 处,并正以 30 海里/时的 航行速度向正东方向匀速行驶,经过 t 小时小艇与轮船相遇.试设计航行方案(即确 定航行方向和航行速度的大小),使得小艇能以最短的时间与轮船相遇,并说明理 由. (1)若希望相遇时小艇航行距离最小,则小艇航行速度为多少? (2)若保证小艇在 30 分钟内(含 30 分钟)与轮船相遇,试求小艇航行速度的最小值. 解析 (1)解法一:设相遇时小艇航行距离为 s 海里,则 s = (30) 2 + 20 2 -2 × 30t · 20cos(90 ° -30 ° ) = 900 2 -600t + 400= 900 - 1 3 2 + 300 , 故当 t= 1 3 时航行距离最小,为 10 3 海里, 此时 v= 10 3 1 3 =30 3 (海里/时), 即小艇以 30 3 海里/时的速度航行,相遇时航行距离最小. 解法二:如图所示, 因为轮船向正东方向匀速行驶,所以小艇航行的最短距离是港口到轮船正东航行 的垂直距离,设相遇点为 B,则△OAB 是直角三角形, 轮船的航行时间 t= sin30 ° 30 = 20 × 1 2 30 = 1 3 (小时), 而小艇的航行距离为 OB=OAcos30°=20× 3 2 =10 3 海里, 此时小艇的航行速度 v= 10 3 1 3 =30 3 (海里/时), 即小艇以 30 3 海里/时的速度航行,相遇时航行距离最小. (2)设小艇航行速度的大小是 v 海里/时,小艇与轮船在 B 处相遇如图所示: 由余弦定理,得 OB2=OA2+AB2-2OA·AB·cos∠OAB, 即(vt)2=202+(30t)2-2×20×30tcos(90°-30°), 化简,得 v2= 400 2 - 600 +900=400 1 - 3 4 2 +675, 由于 0