2021高考数学一轮复习专练59变量的相关关系统计案例含解析理新人教版 6页

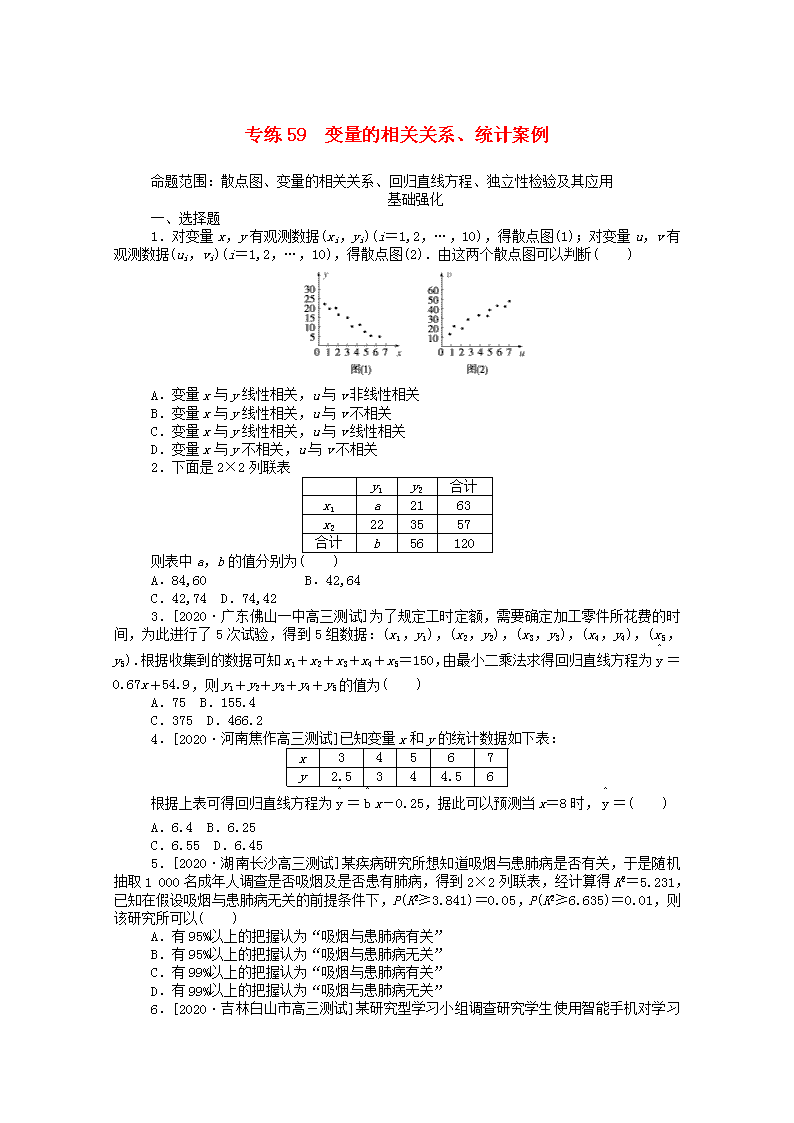
专练59　变量的相关关系、统计案例 命题范围：散点图、变量的相关关系、回归直线方程、独立性检验及其应用 基础强化 一、选择题 ‎1．对变量x，y有观测数据(xi，yi)(i＝1,2，…，10)，得散点图(1)；对变量u，v有观测数据(ui，vi)(i＝1,2，…，10)，得散点图(2)．由这两个散点图可以判断(　　)‎ A．变量x与y线性相关，u与v非线性相关 B．变量x与y线性相关，u与v不相关 C．变量x与y线性相关，u与v线性相关 D．变量x与y不相关，u与v不相关 ‎2．下面是2×2列联表 y1‎ y2‎ 合计 x1‎ a ‎21‎ ‎63‎ x2‎ ‎22‎ ‎35‎ ‎57‎ 合计 b ‎56‎ ‎120‎ 则表中a，b的值分别为(　　)‎ A．84,60　　　　　　　B．42,64‎ C．42,74 D．74,42‎ ‎3．[2020·广东佛山一中高三测试]为了规定工时定额，需要确定加工零件所花费的时间，为此进行了5次试验，得到5组数据：(x1，y1)，(x2，y2)，(x3，y3)，(x4，y4)，(x5，y5)．根据收集到的数据可知x1＋x2＋x3＋x4＋x5＝150，由最小二乘法求得回归直线方程为＝0.67x＋54.9，则y1＋y2＋y3＋y4＋y5的值为(　　)‎ A．75 B．155.4‎ C．375 D．466.2‎ ‎4．[2020·河南焦作高三测试]已知变量x和y的统计数据如下表：‎ x ‎3‎ ‎4‎ ‎5‎ ‎6‎ ‎7‎ y ‎2.5‎ ‎3‎ ‎4‎ ‎4.5‎ ‎6‎ 根据上表可得回归直线方程为＝x－0.25，据此可以预测当x＝8时，＝(　　)‎ A．6.4 B．6.25‎ C．6.55 D．6.45‎ ‎5．[2020·湖南长沙高三测试]某疾病研究所想知道吸烟与患肺病是否有关，于是随机抽取1 000名成年人调查是否吸烟及是否患有肺病，得到2×2列联表，经计算得K2＝5.231，已知在假设吸烟与患肺病无关的前提条件下，P(K2≥3.841)＝0.05，P(K2≥6.635)＝0.01，则该研究所可以(　　)‎ A．有95%以上的把握认为“吸烟与患肺病有关”‎ B．有95%以上的把握认为“吸烟与患肺病无关”‎ C．有99%以上的把握认为“吸烟与患肺病有关”‎ D．有99%以上的把握认为“吸烟与患肺病无关”‎ ‎6．[2020·吉林白山市高三测试]某研究型学习小组调查研究学生使用智能手机对学习的影响，部分统计数据如下表：‎ 使用智能手机 不使用智能手机 总计 学习成绩优秀 ‎4‎ ‎8‎ ‎12‎ 学习成绩不优秀 ‎16‎ ‎2‎ ‎18‎ 总计 ‎20‎ ‎10‎ ‎30‎ 附表：‎ P(K2≥k0)‎ ‎0.15‎ ‎0.10‎ ‎0.05‎ ‎0.025‎ ‎0.010‎ ‎0.005‎ ‎0.001‎ k0‎ ‎2.072‎ ‎2.706‎ ‎3.841‎ ‎5.024‎ ‎6.635‎ ‎7.879‎ ‎10.828‎ 经计算K2的观测值k＝10，则下列选项正确的是(　　)‎ A．有99.5%的把握认为使用智能手机对学习有影响 B．有99.5%的把握认为使用智能手机对学习无影响 C．有99.9%的把握认为使用智能手机对学习有影响 D．有99.9%的把握认为使用智能手机对学习无影响 ‎7．下表是一位母亲给儿子作的成长记录：‎ 年龄/周岁 ‎3‎ ‎4‎ ‎5‎ ‎6‎ ‎7‎ ‎8‎ ‎9‎ 身高/cm ‎94.8‎ ‎104.2‎ ‎108.7‎ ‎117.8‎ ‎124.3‎ ‎130.8‎ ‎139.1‎ 根据以上样本数据，她建立的身高y(cm)与年龄x(周岁)的线性回归方程为＝7.19x＋73.96，给出下列结论：‎ ‎①y与x具有正的线性相关关系；‎ ‎②回归直线过样本点的中心(42,117.1)；‎ ‎③儿子10岁时的身高是‎145.86 cm；‎ ‎④儿子年龄增加1周岁，身高约增加‎7.19 cm.‎ 其中，正确结论的个数是(　　)‎ A．1 B．2‎ C．3 D．4‎ ‎8．某大学舞蹈社团为了解新生对街舞的喜欢是否与性别有关，在全校一年级学生中进行了抽样调查，调查结果如下表所示：‎ 喜欢街舞 不喜欢街舞 总计 男生 ‎184‎ ‎26‎ ‎210‎ 女生 ‎200‎ ‎50‎ ‎250‎ 总计 ‎384‎ ‎76‎ ‎460‎ 根据表中数据，求得K2的观测值k0＝≈4.804，则至少有______%的把握认为对街舞的喜欢与性别有关．(　　)‎ 参考数据：‎ P(K2≥k0)‎ ‎0.15‎ ‎0.10‎ ‎0.05‎ ‎0.025‎ ‎0.010‎ ‎0.005‎ ‎0.001‎ k0‎ ‎2.072‎ ‎2.706‎ ‎3.841‎ ‎5.024‎ ‎6.635‎ ‎7.879‎ ‎10.828‎ A.90 B．95‎ C．97.5 D．99‎ ‎9．[2020·黑龙江高三测试]下列表格所示的五个散点，原本数据完整，且利用最小二乘法求得这五个散点的线性回归直线方程为＝0.8x－155，后因某未知原因使第5组数据的y值模糊不清，此位置数据记为m(如下表所示)，则利用回归方程可求得实数m的值为(　　)‎ x ‎196‎ ‎197‎ ‎200‎ ‎203‎ ‎204‎ y ‎1‎ ‎3‎ ‎6‎ ‎7‎ m A.8.3‎‎ B．8.2‎ C．8.1 D．8‎ 二、填空题 ‎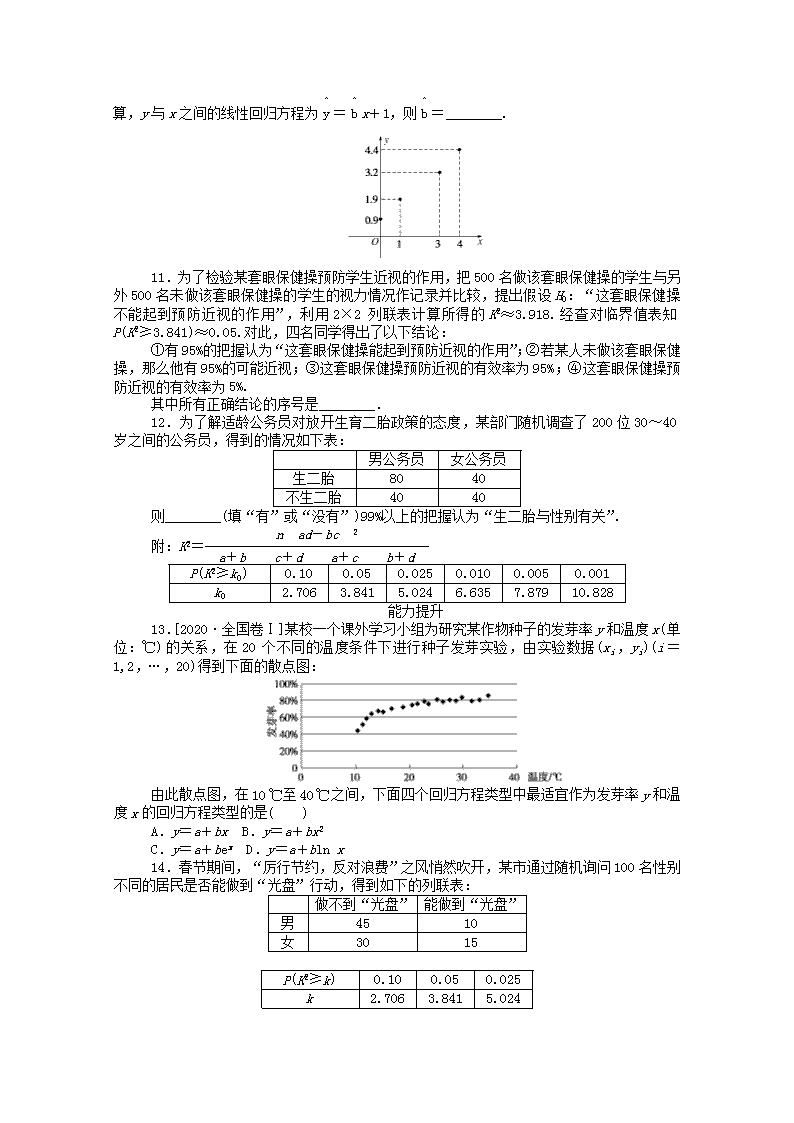10．[2020·广东高三测试]如图是一组数据(x，y ‎)的散点图，经最小二乘法估计公式计算，y与x之间的线性回归方程为＝x＋1，则＝________.‎ ‎11．为了检验某套眼保健操预防学生近视的作用，把500名做该套眼保健操的学生与另外500名未做该套眼保健操的学生的视力情况作记录并比较，提出假设H0：“这套眼保健操不能起到预防近视的作用”，利用2×2列联表计算所得的K2≈3.918.经查对临界值表知P(K2≥3.841)≈0.05.对此，四名同学得出了以下结论：‎ ‎①有95%的把握认为“这套眼保健操能起到预防近视的作用”；②若某人未做该套眼保健操，那么他有95%的可能近视；③这套眼保健操预防近视的有效率为95%；④这套眼保健操预防近视的有效率为5%.‎ 其中所有正确结论的序号是________．‎ ‎12．为了解适龄公务员对放开生育二胎政策的态度，某部门随机调查了200位30～40岁之间的公务员，得到的情况如下表：‎ 男公务员 女公务员 生二胎 ‎80‎ ‎40‎ 不生二胎 ‎40‎ ‎40‎ 则________(填“有”或“没有”)99%以上的把握认为“生二胎与性别有关”．‎ 附：K2＝ P(K2≥k0)‎ ‎0.10‎ ‎0.05‎ ‎0.025‎ ‎0.010‎ ‎0.005‎ ‎0.001‎ k0‎ ‎2.706‎ ‎3.841‎ ‎5.024‎ ‎6.635‎ ‎7.879‎ ‎10.828‎ 能力提升 ‎13．[2020·全国卷Ⅰ]某校一个课外学习小组为研究某作物种子的发芽率y和温度x(单位：℃)的关系，在20个不同的温度条件下进行种子发芽实验，由实验数据(xi，yi)(i＝1,2，…，20)得到下面的散点图：‎ 由此散点图，在‎10 ℃‎至‎40 ℃‎之间，下面四个回归方程类型中最适宜作为发芽率y和温度x的回归方程类型的是(　　)‎ A．y＝a＋bx B．y＝a＋bx2‎ C．y＝a＋bex D．y＝a＋bln x ‎14．春节期间，“厉行节约，反对浪费”之风悄然吹开，某市通过随机询问100名性别不同的居民是否能做到“光盘”行动，得到如下的列联表：‎ 做不到“光盘”‎ 能做到“光盘”‎ 男 ‎45‎ ‎10‎ 女 ‎30‎ ‎15‎ P(K2≥k)‎ ‎0.10‎ ‎0.05‎ ‎0.025‎ k ‎2.706‎ ‎3.841‎ ‎5.024‎ 附：K2＝ 参照附表，得到的正确结论是(　　)‎ A．在犯错误的概率不超过1%的前提下，认为“该市居民能否做到‘光盘’与性别有关”‎ B．在犯错误的概率不超过1%的前提下，认为“该市居民能否做到‘光盘’与性别无关”‎ C．有90%以上的把握认为“该市居民能否做到‘光盘’与性别有关”‎ D．有90%以上的把握认为“该市居民能否做到‘光盘’与性别无关”‎ ‎15．在西非肆虐的“埃博拉病毒”的传播速度很快，已经成为全球性的威胁，为了考察某种埃博拉病毒疫苗的效果，现随机抽取100只小鼠进行试验，得到如下列联表：‎ 感染 未感染 总计 服用 ‎10‎ ‎40‎ ‎50‎ 未服用 ‎20‎ ‎30‎ ‎50‎ 总计 ‎30‎ ‎70‎ ‎100‎ 参考公式：K2＝ P(K2‎>k)‎ ‎0.15‎ ‎0.10‎ ‎0.05‎ ‎0.025‎ ‎0.010‎ ‎0.005‎ ‎0.001‎ k ‎2.072‎ ‎2.706‎ ‎3.841‎ ‎5.024‎ ‎6.635‎ ‎7.879‎ ‎10.828‎ 参照附表，在犯错误的概率最多不超过________(填百分比)的前提下，可认为“该种疫苗有预防埃博拉病毒感染的效果”．‎ ‎16．某电子产品的成本价格由两部分组成，一是固定成本，二是可变成本，为确定该产品的成本，进行5次试验，收集到的数据如表：‎ 产品数x个 ‎10‎ ‎20‎ ‎30‎ ‎40‎ ‎50‎ 产品总成本(元)‎ ‎62‎ a ‎75‎ ‎81‎ ‎89‎ 由最小二乘法得到回归方程＝0.67x＋54.9，则a＝________.‎ 专练59　变量的相关关系、统计案例 ‎1．C　由散点图知，这些点都分布在条形区域内，具有相关关系．‎ ‎2．B　由列联表可知a＋21＝63，∴a＝42，‎ b＝a＋22＝42＋22＝64.‎ ‎3．C　由题意可得：＝＝30，‎ 线性回归方程过样本中心点，则：＝0.67×＋54.9＝75，据此可知：y1＋y2＋y3＋y4＋y5＝5＝375.‎ ‎4．C　∵＝＝5，＝＝4，‎ 又(，)在＝x－0.25，‎ ‎∴4＝5－0.25，∴＝0.85，‎ ‎∴回归方程为＝0.85x－0.25，‎ ‎∴当x＝8时，＝6.55.‎ ‎5．A　由独立性检验的结论结合题意可知：有95%以上的把握认为“吸烟与患肺病有关”．‎ ‎6．A　由于K2的观测值k＝10>7.879，其对应的值0.005＝0.5%，‎ 据此结合独立性检验的思想可知：有99.5%的把握认为使用智能手机对学习有影响．‎ ‎7．B　由于线性回归方程为＝7.19x＋73.96，7.19>0，即y随x的增大而增大，y与x具有正的线性相关关系，①正确；由计算可得，样本点的中心为(6,117.1)，②错误；当x＝10时，＝145.86，此为估计值，所以儿子10岁时的身高的估计值是‎145.86 cm，而不一定是实际值，③错误；由于回归直线的斜率为7.19，则儿子年龄增加1周岁，身高约增加‎7.19 cm，④正确，故应选B.‎ ‎8．B　由题意知，4.804>3.841，所以至少有95%的把握认为对街舞的喜欢与性别有关．‎ ‎9．D　由题意可得：‎ ＝＝200，‎ ＝＝，‎ 回归方程过样本中心点，则：‎ ＝0.8×200－155，解得：m＝8.‎ ‎10．0.8‎ 解析：＝＝2，‎ ＝＝2.6，‎ 又＝x＋1过(，)，‎ ‎∴2.6＝2＋1，‎ ＝0.8.‎ ‎11．①‎ 解析：根据查对临界值表知P(K2≥3.841)≈0.05，故有95%的把握认为“这套眼保健操能起到预防近视的作用”，即①正确；95%仅指“这套眼保健操能起到预防近视的作用”的可信程度，所以②③④错误．‎ ‎12．没有 解析：由于K2＝＝‎ eq f(200×(80×40－40×40)2,120×80×120×80)＝<6.635，故没有99%以上的把握认为“生二胎与性别有关”．‎ ‎13．D　本题考查回归方程及一次函数、二次函数、指数型函数、对数型函数的图象，观察散点图可知，散点图用光滑曲线连接起来比较接近对数型函数的图象．故选D.‎ ‎14．C　由2×2列联表得到a＝45，b＝10，c＝30，d＝15，则a＋b＝55，c＋d＝45，a＋c＝75，b＋d＝25，ad＝675，bc＝300，n＝100.代入K2＝，得K2的观测值k＝≈3.030.因为2.706<3.030<3.841.所以有90%以上的把握认为“该市民能否做到‘光盘’与性别有关．故选C.‎ ‎15．5%‎ 解析：由题意可得，K2＝≈4.762>3.841，参照附表可得，在犯错误的概率不超过5%的前提下，可认为“该种疫苗有预防埃博拉病毒感染的效果”．‎ ‎16．68‎ 解析：计算可得，＝30，＝，所以＝0.67×30＋54.9，解得a＝68.‎