2020_2021学年新教材高中数学第五章三角函数5 35页

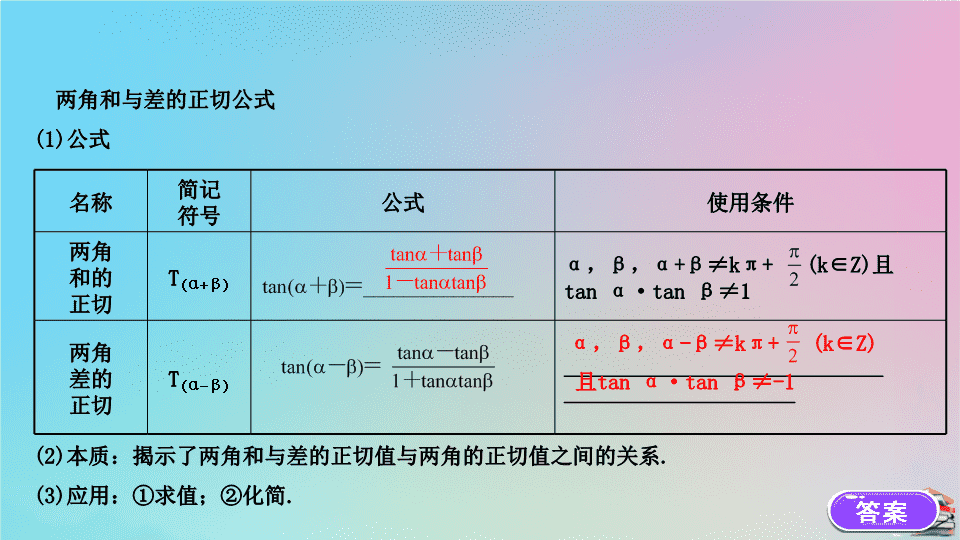
第 3 课时　两角和与差的正弦、余弦、正切公式 ( 二 ) 　　 必备知识 · 自主学习 导思 1. 两角和与差的正切公式的形式是怎样的？ 2. 两角和与差的正切公式有哪些应用？ 　两角和与差的正切公式 (1) 公式 (2) 本质：揭示了两角和与差的正切值与两角的正切值之间的关系 . (3) 应用：①求值；②化简 . 名称 简记 符号 公式 使用条件 两角 和的 正切 T (α+β) α ， β ， α+β≠kπ+ (k∈Z) 且 tan α·tan β≠1 两角 差的 正切 T (α-β) _____________________________ _____________________ α ， β ， α-β≠kπ+ (k∈Z) 且 tan α·tan β≠-1 　 【 思考 】 (1) 由同角三角函数的商数关系知 tan(α+β)= ，由此能否推导出两角 和的正切公式？若能，写出推导过程 . 提示： 能 . tan( α + β )= ，分子分母同除以 cos α cos β ，可 得 tan( α + β )= (2) 两角和与差的正切公式中为什么限制 α ， β ， α+β ， α-β 都不等于 kπ + (k∈Z) ？ 提示： 这是由正切函数的定义域决定的 . 【 基础小测 】 1. 辨析记忆 ( 对的打“√”，错的打“ ×”) (1) 存在 α ， β∈R ，使 tan(α+β)=tan α+tan β 成立 . ( 　　 ) (2) 对任意 α ， β∈R ， tan(α+β)= 都成立 . ( 　　 ) (3)tan(α+β)= 等价于 tan α+tan β= tan( α + β )· (1-tan α tan β ).( 　　 ) 提示： (1)√. 当 α =0 ， β = 时， tan( α + β )= ，但一般情况下不成立 . (2) × . 两角和的正切公式的适用范围是 α ， β ， α + β ≠k π + (k∈Z) 且 tan α ·tan β ≠1. (3)√. 当 α ≠k π + (k∈Z) ， β ≠k π + (k∈Z) ， α + β ≠k π + (k∈Z) 时， 由前一个式子两边同乘以 1-tan α tan β 可得后一个式子 . 2.( 教材二次开发：例题改编 ) 已知 cos α=- ， α∈ ，则 tan = ( 　　 ) 　　　　　　　　　　　　　　　　　 A. B.7 C.- D.-7 【 解析 】 选 B. 因为 cos α =- ， α ∈ ，所以 α ∈ ，所以 sin α = - ， tan α = ， 则 tan 3. = ( 　　 ) 【 解析 】 选 C. 关键能力 · 合作学习 类型一　给角求值问题 ( 数学运算 ) 【 题组训练 】 1.(2019· 全国卷 Ⅰ)tan 255°= ( 　　 ) A.-2- B.-2+ C.2- D.2+ 2. 计算： =_______.  3.tan 10°+tan 50°+ tan 10°tan 50°=_______.  【 解析 】 1. 选 D.tan 255 ° =tan(180 ° +75 ° )=tan 75 ° =tan(30 ° +45 ° ) = 2. 原式 = 答案： 1 3. 因为 tan 60 ° =tan(10 ° +50 ° )= 所以 tan 10 ° +tan 50 ° =tan 60 ° (1-tan 10 ° tan 50 ° ) = - tan 10 ° tan 50 ° ，所以原式 = - tan 10 ° tan 50 ° + tan 10 ° tan 50 ° = . 答案： 【 解题策略 】 公式 T (α+β) ， T (α-β) 应用的解题策略 (1) 公式 T (α+β) ， T (α-β) 有 tan α·tan β ， tan α+tan β( 或 tan α-tan β) ， tan(α+β)( 或 tan(α-β)) ，三者知二可求出第三个 . (2) 化简过程中注意“ 1” 与“ tan ” ，“ ”与“ tan ” 等特殊数与特殊 角的函数值之间的转化 . 　　 【 补偿训练 】 tan 72°-tan 42°- tan 72°tan 42°=_______.  【 解析 】 原式 =tan(72 ° -42 ° )(1+tan 72 ° ·tan 42 ° )- tan 72 ° tan 42 ° =tan 30 ° (1+tan 72 ° tan 42 ° )-tan 30 ° tan 72 ° tan 42 ° =tan 30 ° = . 答案： 类型二　给值求角问题 ( 数学运算 ) 【 典例 】 (2020· 洛阳高一检测 ) 已知 tan =2 ， tan(α-β)= ， α∈ (1) 求 tan α 的值； (2) 求 2α-β 的值 . 【 解题策略 】 给值求角问题的步骤及选取函数的原则 (1) 给值求角问题的步骤 . ① 求所求角的某个三角函数值 . ② 确定所求角的范围 ( 范围过大或过小，会使求出的角不合题意或漏解 ) ，根据 范围找出角 . (2) 选取函数的原则 . ① 已知正切函数值，选正切函数 . ② 已知正余弦函数值，选正弦或余弦函数，若角的范围是 ，选正弦或余弦 函数均可；若角的范围是 (0 ， π) ，选余弦较好；若角的范围是 ，选正弦 较好 . 　 【 跟踪训练 】 已知 tan α= ， sin β= ，且 α ， β 为锐角，求 α+2β 的值 . 【 解析 】 因为 tan α = <1 且 α 为锐角， 所以 0< α < . 又因为 sin β = 且 β 为锐角 . 所以 0< β < ， 所以 0< α +2 β < . ① 由 sin β = ， β 为锐角，得 cos β = ， 所以 tan β = . 所以 tan( α + β )= 所以 tan( α +2 β )= 由 ①② 可得 α +2 β = . 【 补偿训练 】 已知 α ， β ， γ 都是锐角，且 tan α= ， tan β= ， tan γ= ，则 α+β+γ=_______.  【 解析 】 因为 tan( α + β )= tan( α + β + γ )= 因为 tan α = ，且 α 为锐角， 所以 0< α < ，同理 0< β < ， 0< γ < ， 所以 0< α + β + γ < ，所以 α + β + γ = . 答案： 类型三　给值求值问题 ( 数学运算 ) 　角度 1 　式子变换  【 典例 】 已知 sin α= ， α∈ ， tan(π-β)= ，则 tan(α-β) 的值 为 ( 　　 ) 　　　　　 　　　　　 　　　　　 【 思路导引 】 由条件得出 tan α 与 tan β 的值，代入两角差的正切公式可求值 . 【 解析 】 选 A. 因为 α ∈ ， sin α = ， 所以 cos α =- ， tan α =- ，又 tan β =- ， 所以 tan( α - β )= 　 　 【 变式探究 】 本例条件不变，求 tan(α+β) 的值 . 【 解析 】 因为 α ∈ ， sin α = ，所以 cos α =- ， tan α =- ，又 tan β =- ， 所以 tan( α + β )= 　角度 2 　拆角变换  【 典例 】 已知 tan α= ， tan(α-β)=- ，那么 tan(β-2α) 的值为 ( 　　 ) 【 思路导引 】 tan(β-2α)=-tan(2α-β)=-tan 【 解析 】 选 B.tan( β -2 α )=-tan(2 α - β ) 【 解题策略 】 给值求值问题的两种变换 (1) 式子的变换：分析已知式子的结构特点，结合两角和与差的三角函数公式，通过变形，建立与待求式子间的联系以实现求值 . (2) 角的变换：首先从已知角间的关系入手，分析已知角与待求角间的关系，如用 α=β-(β-α) 、 2α=(α+β)+(α-β) 等关系，把待求的三角函数与已知三角函数巧妙地建立等量关系，从而求值 . 【 题组训练 】 1. 若 tan α=2 ， tan β= ，则 tan(α+β) 等于 ( 　　 ) A.1 B.-1 C.7 D.-7 【 解析 】 选 C.tan( α + β )= 2. 已知 tan ，则 tan(α+β) 的值为 ( 　　 ) 【 解析 】 选 D. 因为 tan 所以 tan( α + β ) 课堂检测 · 素养达标 1. 已知 tan α=- ，则 tan 等于 ( 　　 ) A.- B.-7 C. D.7 【 解析 】 选 D.tan 2.tan α=2 ， tan β=3 ，则 tan(α-β)= ( 　　 ) A.-7 B. C.- D.- 【 解析 】 选 D.tan( α - β )= 3. 已知 α ， β 都是锐角， tan α= ， tan β= ，则 α+β 的值为 ( 　　 ) 【 解析 】 选 C.tan( α + β )= 又因为 α ， β 都是锐角，所以 α + β ∈(0 ， π ) ，所以 α + β = . 4.( 教材二次开发：练习改编 ) 求值： (1)tan(-75°)=_______ ；   (2) =_______.  【 解析 】 (1)tan 75 ° =tan(45 ° +30 ° )= 所以 tan(-75 ° )=-tan 75 ° =-2- . (2) 原式 =tan(74 ° +76 ° )=tan 150 ° =- . 答案： (1)-2- 　 (2)- 5. 计算 =_______.  【 解析 】 答案： 1