高考数学（理）一轮复习人教A版-第四章 第7节 28页

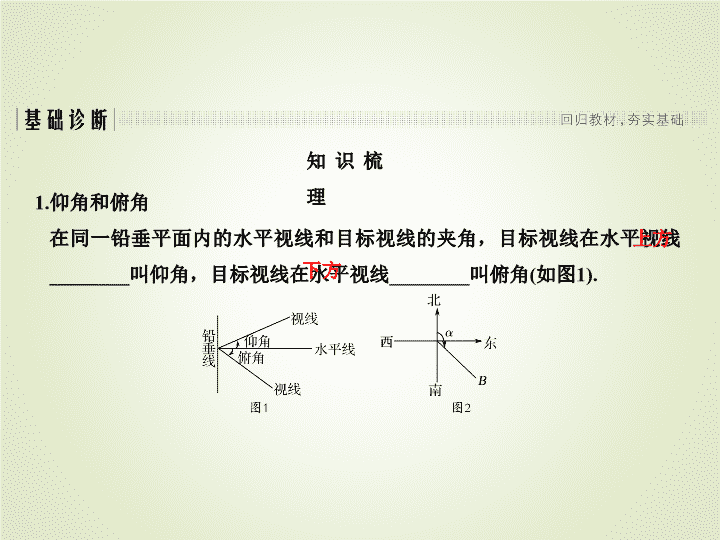
第7节　解三角形应用举例 最新考纲　能够运用正弦定理、余弦定理等知识方法解决一些与测量、 几何计算有关的实际问题. 1.仰角和俯角 在同一铅垂平面内的水平视线和目标视线的夹角，目标视线在水平视线 ________叫仰角，目标视线在水平视线________叫俯角(如图1). 知 识 梳 理 上方 下方 2.方位角 从正北方向起按顺时针转到目标方向线之间的水平夹角叫做方位角.如B 点的方位角为α(如图2). 3.方向角：正北或正南方向线与目标方向线所成的锐角，如南偏东30°， 北偏西45°等. 4.坡度：坡面与水平面所成的二面角的正切值. [常用结论与微点提醒] 1.不要搞错各种角的含义，不要把这些角和三角形内角之间的关系弄混. 2.在实际问题中，可能会遇到空间与平面(地面)同时研究的问题，这时最 好画两个图形，一个空间图形，一个平面图形，这样处理起来既清楚又 不容易出现错误. 诊 断 自 测 解析　(2)α＝β；(3)俯角是视线与水平线所构成的角. 答案　(1)√　(2)×　(3)×　(4)√ 2.若点A在点C的北偏东30°，点B在点C的南偏东60°，且AC＝BC，则点 A在点B的(　　) A.北偏东15° B.北偏西15° C.北偏东10° D.北偏西10° 解析　如图所示，∠ACB＝90°， 又AC＝BC，∴∠CBA＝45°，而β＝30°， ∴α＝90°－45°－30°＝15°. ∴点A在点B的北偏西15°. 答案　B 3.(必修5P24A5改编)如图所示，设A，B两点在河的两岸，一测量者在A所 在的同侧河岸边选定一点C，测出AC的距离为50 m，∠ACB＝45°， ∠CAB＝105°后，就可以计算出A，B两点的距离为(　　) 答案　A 4.轮船A和轮船B在中午12时同时离开海港C，两船航行方向的夹角为120°， 两船的航行速度分别为25 n mile/h，15 n mile/h，则下午2时两船之间的距 离是______n mile. 解析　设两船之间的距离为d， 则d2＝502＋302－2×50×30×cos 120°＝4 900， ∴d＝70，即两船相距70 n mile. 答案　70 5.(2014·全国Ⅰ卷)如图所示，为测量山高MN，选择A和另一座山的山顶C为 测量观测点.从A点测得M点的仰角∠MAN＝60°，C点的仰角∠CAB＝ 45°以及∠MAC＝75°；从C点测得∠MCA＝60°.已知山高BC＝100 m， 则山高MN＝________m. 解析　在Rt△ABC中，∠CAB＝45°，BC＝100 m， 在△ AMC中，∠MAC＝75°，∠MCA＝60°， 从而∠AMC＝45°， 答案　150 考点一　测量高度问题 【例1】 如图所示，一辆汽车在一条水平的公路上向正西行驶，到A处时测 得公路北侧一山顶D在西偏北30°的方向上，行驶600 m后到达B处，测得 此山顶在西偏北75°的方向上，仰角为30°，则此山的高度CD＝ ________m. 规律方法　1.在处理有关高度问题时，要理解仰角、俯角(它是在铅垂面上 所成的角)、方向(位)角(它是在水平面上所成的角)是关键. 2.在实际问题中，可能会遇到空间与平面(地面)同时研究的问题，这时最 好画两个图形，一个空间图形，一个平面图形，这样处理起来既清楚又不 容易搞错. 3.注意山或塔垂直于地面或海平面，把空间问题转化为平面问题. 【训练1】 如图所示，为了估测某塔的高度，在同一水平面的A，B两点 处进行测量，在点A处测得塔顶C在西偏北20°的方向上，仰角为60°； 在点B处测得塔顶C在东偏北40°的方向上，仰角为30°.若A，B两点相 距130 m，求塔的高度CD. 在△ADB中，∠ADB＝180°－20°－40°＝120°， ∴由余弦定理AB2＝BD2＋AD2－2BD·AD·cos 120°， 解　∵∠ADC＝∠ADB＋∠CDB＝60°，∠ACD＝60°， 在△BCD中，∠DBC＝45°，由正弦定理， 在△ABC中，由余弦定理，得AB2＝AC2＋BC2－2AC·BCcos 45° 规律方法　1.选定或确定要创建的三角形，首先确定所求量所在的三角形， 若其他量已知则直接求解；若有未知量，则把未知量放在另一确定三角形 中求解. 2.确定用正弦定理还是余弦定理，如果都可用，就选择更便于计算的定理. 【训练2】 海轮“和谐号”从A处以每小时21海里的速度出发，海轮“奋 斗号”在A处北偏东45°的方向，且与A相距10海里的C处，沿北偏东 105°的方向以每小时9海里的速度行驶，则海轮“和谐号”与海轮“奋 斗号”相遇所需的最短时间为________小时. 解析　设海轮“和谐号”与海轮“奋斗号”相遇所需的最短时间为x小时， 如图， 则由已知得△ ABC中，AC＝10，AB＝21x，BC＝9x，∠ACB＝120°. 由余弦定理得：(21x)2＝100＋(9x)2－2×10×9x×cos 120°， 整理，得36x2－9x－10＝0， 考点三　测量角度问题 【例3】 如图所示，位于A处的信息中心获悉：在其正东方向相距40海里的 B处有一艘渔船遇险，在原地等待营救.信息中心立即把消息告知在其南 偏西30°、相距20海里的C处的乙船，现乙船朝北偏东θ的方向沿直线CB 前往B处救援，则cos θ的值为________. 解析　在△ ABC中，AB＝40，AC＝20，∠BAC＝120°， 由余弦定理得 规律方法　解决测量角度问题的注意事项 (1)首先应明确方位角或方向角的含义. (2)分析题意，分清已知与所求，再根据题意画出正确的示意图，这是最 关键、最重要的一步. (3)将实际问题转化为可用数学方法解决的问题后，注意正弦、余弦定理 的结合使用. 【训练3】 如图，两座相距60 m的建筑物AB，CD的高度分别为20 m，50 m，BD为水平面，则从建筑物AB的顶端A看建筑物CD的张角∠CAD等 于(　　) A.30° B.45° C.60° D.75° 所以从顶端A看建筑物CD的张角为45°. 答案　B