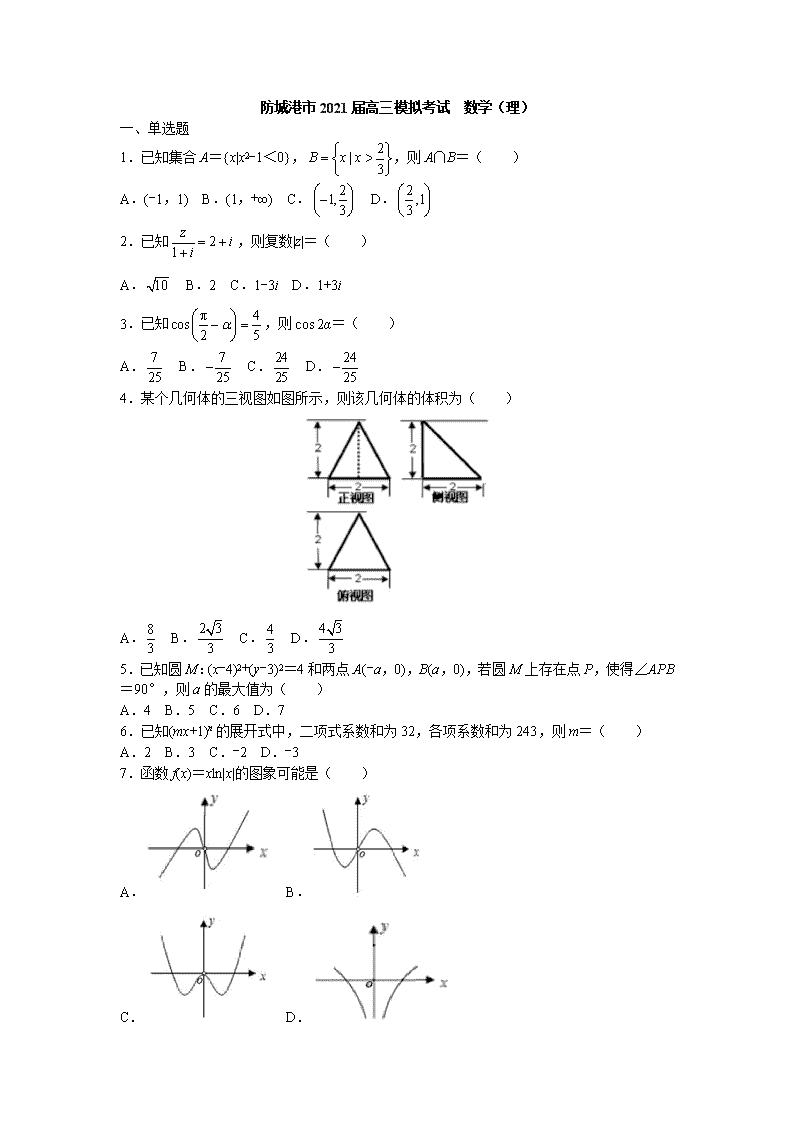广西防城港市2021届高三上学期12月模拟考试数学（理）试题 Word版含答案 9页

防城港市 2021 届高三模拟考试 数学（理） 一、单选题 1．已知集合 A＝{x|x2-1＜0}， 2| 3B x x     ，则 A∩B＝（ ） A．(-1，1) B．(1，+∞) C． 21, 3     D． 2 ,13      2．已知 21 z ii   ，则复数|z|＝（ ） A． 10 B．2 C．1-3i D．1+3i 3．已知 π 4cos 2 5      ，则 cos 2α＝（ ） A． 7 25 B． 7 25  C． 24 25 D． 24 25  4．某个几何体的三视图如图所示，则该几何体的体积为（ ） A． 8 3 B． 2 3 3 C． 4 3 D． 4 3 3 5．已知圆 M：(x-4)2+(y-3)2＝4 和两点 A(-a，0)，B(a，0)，若圆 M 上存在点 P，使得∠APB ＝90°，则 a 的最大值为（ ） A．4 B．5 C．6 D．7 6．已知(mx+1)n 的展开式中，二项式系数和为 32，各项系数和为 243，则 m＝（ ） A．2 B．3 C．-2 D．-3 7．函数 f(x)＝xln|x|的图象可能是（ ） A． B． C． D． 8．已知随机变量ξ服从正态分布 N(1，σ2)，且 P(ξ＜0)＝P(ξ＞a-3)，则 a＝（ ） A．-2 B．2 C．5 D．6 9．已知△ABC 的三边满足条件 2 2( ) 3a b c bc    ，则∠A＝（ ） A．30° B．45° C．60° D．120° 10．已知 π ,06      为 π( ) sin( 2 ) | | 2f x x         的一个对称中心，则f(x)的对称轴可能为（ ） A． π 2x  B． π 12x   C． π 3x   D． 2π 3x  11．已知双曲线 C： 2 2 2 2 1( 0, 0)x y a ba b     的左、右焦点分别为 F1、F2，过 F2 作垂直于实 轴的弦 PQ，若 1 π 2PFQ  ，则 C 的离心率 e 为（ ） A． 2 1 B． 2 C． 2 1 D． 2 2 12．已知函数 2 2 2 , 0( ) 2 , 0x x x a xf x e ax e x         在 R 恰有两个零点，则实数 a 的取值范围是（ ） A．(0，1) B．(e，+∞) C． (0,1) ,2 e    D． 2 (0,1) ,2 e      二、填空题 13．已知向量 (1,1)a  ， ( 3,2)b   ，若 2ka b  与 a  垂直，则实数 k＝__________． 14．若变量 x、y 满足约束条件 2 0 2 0 y x y x y         ，则 z＝x+2y 的最大值为__________． 15．在三棱锥中 P-ABC，PA，PB，PC 两两相互垂直，PA＝PB＝PC＝1，则此三棱锥内切 球的半径为__________． 16．已知抛物线 C：y2＝x，过 C 的焦点的直线与 C 交于 A，B 两点．弦 AB 长为 2，则线段 AB 的中垂线与 x 轴交点的横坐标为__________． 三、解答题 17．已知数列{an}的前 n 项和为 Sn，且 Sn+2＝2an． （1）求数列{an}的通项公式； （2）若 bn＝nan，求数列{bn}的前 n 项和 Tn． 18．在四棱锥 P-ABCD 中，侧面 PAD⊥底面 ABCD，底面 ABCD 为直角梯形，BC∥AD，∠ ADC＝90°， 1 12BC CD AD   ，PA＝PD，E，F 分别为 AD，PC 的中点． （Ⅰ）求证：PA∥平面 BEF； （Ⅱ）若 PE＝EC，求二面角 F-BE-A 的余弦值． 19．某超市准备举办一次有奖促销活动，若顾客一次消费达到 400 元则可参加一次抽奖活动， 超市设计了两种抽奖方案． 方案一：一个不透明的盒子中装有 15 个质地均匀且大小相同的小球，其中 5 个红球，10 个 白球，搅拌均匀后，顾客从中随机抽取一个球，若抽到红球则顾客获得 80 元的返金券，若 抽到白球则获得 20 元的返金券，且顾客有放回地抽取 3 次． 方案二：一个不透明的盒子中装有 15 个质地均匀且大小相同的小球，其中 5 个红球，10 个 白球，搅拌均匀后，顾客从中随机抽取一个球，若抽到红球则顾客获得 100 元的返金券，若 抽到白球则未中奖，且顾客有放回地抽取 3 次． （1）现有两位顾客均获得抽奖机会，且都按方案一抽奖，试求这两位顾客均获得 240 元返 金券的概率； （2）若某顾客获得抽奖机会． ①试分别计算他选择两种抽奖方案最终获得返金券的数学期望； ②该顾客选择哪一种抽奖方案才能获得更多的返金券？ 20．在平面直角坐标系 xOy 中，椭圆 2 2 2 2 1( 0)x y a ba b     的离心率为 3 2 ，过椭圆右焦点 F 作两条互相垂直的弦 AB 与 CD，当直线 AB 的斜率为 0 时，|AB|+|CD|＝5． （1）求椭圆的方程； （2）求由 A，B，C，D 四点构成的四边形面积的取值范围． 21．已知函数 1( ) ln 1 xf x axx   ． （1）讨论 f(x)的单调性； （2）当时 x∈(0，1)， 2 4 1 ax ax xe e x    ，求实 a 数的取值范围． 选做题： 22．在直角坐标系 xOy 中，直线 l 的参数方程为 11 2 3 2 x t y t      （t 为参数），在以坐标原点 O 为极点，x 轴的正半轴为极轴的极坐标系中，曲线 C 的极坐标方程为ρ2(1+3cos2θ)＝4． （1）写出直线 l 的普通方程与曲线 C 的直角坐标方程； （2）设点 M(1，0)．若直线 l 与曲线 C 相交于不同的两点 A，B，求|AM|+|BM |的值． 23．已知函数 f(x)＝|x+1|． （1）求不等式 f(x)＜|2x+1|-1 的解集； （2）关于 x 的不等式 f(x-2)+f(x-3)＜a 的解集不是空集，求实数 a 的取值范围． 防城港市 2021 届高三模拟考试 数学（理） 参考答案 1．D【详解】由已知 A＝{x|x2-1＜0}＝{x|-1＜x＜1}，又 2| 3B x x     ，则 2 ,13A B      ．故 选：D． 2．A【详解】由题意可得：z＝(2+i)(1+i)＝1+3i，则| | 1 9 10z    ．本题选择 A 选项． 3．B【详解】由题意结合诱导公式可得： π 4sin cos 2 5        ，则 2cos2 1 2sin 1    24 72 5 25        ． 4．C【详解】由三视图可知，几何体为高为 2 的三棱锥∴三棱锥体积： 1 1 1 23 3 2V Sh    42 2 3    选项：C 5．D【详解】若点 P 满足∠APB＝90°，则点 P 在以 AB 为直径的圆上，据此可知，满足题 意时，圆 x2+y2＝a2 与圆(x-4)2+(y-3)2＝4 有公共点，两圆的圆心距： 2 2(0 4) (0 3) 5d      ， 两圆的半径 r1＝a，r2＝2，满足时应有：|r1-r2|≤d≤|r1+r2|，即：|a-2|≤5≤|a+2|，求解关于 实数 a 的不等式可得：3≤a≤7，则 a 的最大值为 7． 6．A【详解】展开式二项式系数和为 32，则：2n＝32，故 n＝5．则各项系数和为(m×1+1)5 ＝243，据此可得：m＝2． 7．A【详解】函数的定义域{x|x≠0}关于坐标原点对称，且由函数的解析式可知： f(-x)＝ -x×ln|-x|＝-xln x＝-f(x)，则函数 f(x)为奇函数，其图象关于坐标原点对称，选项 CD 错误； 当 x＞0 时，f(x)＝xln x，则 1( ) ln ln 1f x x x xx       ，当 10,x e     时，f′(x)＜0，f(x)单调 递减， 当 1 ,x e      时，f′(x)＞0，f(x)单调递增，即函数 f(x)在区间(0，+∞)内先单调递减， 再单调递增，据此可排除 B 选项，本题选择 A 选项． 8．C【详解】随机变量ξ服从正态分布 N(1，σ2)，则正态分布的图象关于直线 x＝1 对称， 结 合 P(ξ＜0)＝P(ξ＞a-3)有 0 ( 3) 12 a   ，解得：a＝5．本题选择 C 选项． 9．D【详解】由 2 2( ) 3a b c bc    可得：(b-c)2-a2＝-3bc，则 2 2 2 1cos 2 2 b c aA bc     ，据此 可得∠A＝120°． 10．B【详解】由题意可知，当 π 6x  时， π2 2 π( )6x k k Z         ，据此可得： πk   π ( )3 k Z ，令 k＝0 可得 π 3   ，则函数的解析式为 π π( ) 2 sin 23 3f x x x               ，函数 的对称轴满足： π π2 π ( )3 2x k k Z    ，解得： π 5π ( )2 12 kx k Z   ，令 k＝-1 可知函数的一 条对称轴为 π 12x   ，且很明显选项 ACD 不是函数 f(x)的对称轴．本题选择 B 选项． 11．C【详解】双曲线的左右焦点分别为 F1、F2，过 F2 作垂直于实轴的弦 PQ，若 1 π 2PFQ  ， 则：△PF1Q 为等腰直角三角形．由于通径 22bPQ a  ，则： 2 2 bc a  ，解得：c2-a2-2ac＝0， 所以：e2-2e-1＝0， 解得： 1 2e   ；由于 e＞1，所以： 1 2e   ，故选：C． 12．D 解：当 x＝0 时，f(x)＝-1-e2≠0，故 0 不是函数的零点；当 x∈(0，+∞)时，f(x)＝0 等 价于 2 2 xe ea x  ．令 2 ( ) xe eg x x  ，则 2 2( ) x xxe e eg x x    ．当 x＜2 时，g′(x)＜0，当 x＝2 时，g′(x)＝0，当 x＞2 时，g′(x)＞0，∴g(x)≥e2，即 2a≥e2， 2 2 ea  ． ①当 0＜a＜1 时， f(x)在(-∞，0)上有两个零点，则 f(x)在(0，+∞)无零点，则 2 2 ea  ，∴0＜a＜1； ②当 a≤0 或 a＝1 时，f(x)在(-∞，0)上有一个零点，故 f(x)在(0，+∞)上需要有一个零点，此时不合题 意； ③当 a＞1 时，f(x)在(-∞，0)上无零点，故 f(x)在(0，+∞)上需要有两个零点，则 2 2 ea  ． 综 上，实数 a 的取值范围是 2 (0,1) ,2 e      ．故选：D． 13．-1【详解】由平面向量的坐标运算可得： 2 (1,1) 2( 3,2) ( 6, 4)ka b k k k        ， 2ka b  与 a  垂直，则 ( 2 ) 0ka b a     ，即：(k+6)×1+(k-4)×1＝0，解得：k＝-1． 14．8【详解】绘制不等式组表示的可行域如图所示，结合目标函数的几何意义可得目标函 数在点 B(4，2)处取得最大值，其最大值为：zmax＝4+2×2＝8． 15． 1 3 3 或 3 3 6  【详解】由题意可知，三棱锥的三个面是直角边长为 1 的等腰直角三 角形，一个面是边长为 2 的等边三角形，则三棱锥的表面积为： 1 13 1 12 2S          2 2 sin60  °，设三棱锥的内切球半径为 R，利用等体积法可知： 1 1 1 1 13 2SR         ， 即： 1 1 1 13 1 1 2 2 sin60 1 1 12 2 3 2R                        ° ，解得： 1 3 3 R   ，即 R  3 3 6  ． 16．5 4 【详解】设直线 AB 的倾斜角为θ，由抛物线的焦点弦公式有： 2 2 2 1| | 2sin sin pAB     ， 则 2 1sin 2   ，tan2θ＝1，由抛物线的对称性，不妨取直线 AB 的斜率 k＝tan θ＝1，则直线 AB 的方程为： 1 4y x  ，与抛物线方程联立可得： 2 3 1 02 16x x   ，由韦达定理可得： 1 2x x 3 2  ，设 AB 的中点 M(xM，yM)，则 1 2 3 2 4M x xx   ， 1 1 4 2M My x   ，其垂直平分线方程 为： 1 3 2 4y x       ， 令 y＝0 可得 5 4x  ，即线段 AB 的中垂线与 x 轴交点的横坐标为 5 4 ． 17．【解】（1）∵Sn+2＝2an①∴Sn-1+2＝2an-1，(n≥2)② ①-②得 Sn-Sn-1＝2an-2an-1＝an， 则 1 2( 2)n n a na    ，在①式中，令 n＝1，得 a1＝2．∴数列{an}是首项为 2，公比为 2 的等比 数列，∴an＝2n； （2）bn＝n·2n．所以 Tn＝1·21+2·22+3·23+…+(n-1)·2n-1+n·2n③ 则 2Tn＝1·22+2·23+… +(n-2)·2n-1+(n-1)·2n+n·2n+1④ ③-④得， 2 3 1 1 2 (1 22 2 2 2 2 )2 2 1 n n n n nT n              … 1 12 2 (1 2 2)n n nn n         ∴Tn＝(n-1)·2n+1+2． 18．【解】（1）连接 AC 交 BE 于 O，并连接 EC，FO，∵BC∥AD， 1 2BC AD ，E 为 AD 中点，∴AE∥BC，且 AE＝BC，∴四边形 ABCE 为平行四边形，∴O 为 AC 中点，又 F 为 PC 中点，∴OF∥PA，∵OF ⊂ 平面 BEF，PA ⊄ 平面 BEF，∴PA∥平面 BEF． （2）由题意可知 PE⊥面 ABCD，BE⊥AD，如图所示，以 E 为原点，EA、EB、EP 分别为 x、y、z 建立直角坐标系，则 E(0，0，0)，A(1，0，0)，B(0，1，0)， 1 1 2, ,2 2 2F      ．平面 ABE 法向量可取： (0,0,1)n  ，平面 FBE 中，设法向量为 ( , , )m a b c ， 则 0 0 m EB m EF           0 0 0 1 1 2 02 2 2 b a b c       ，取 ( 2,0,1)m  ， 1cos , | || | 3 m nm n m n          ，所以二面角 F-BE-A 的 余弦值为 3 3  ． 19．（1）选择方案一，则每一次摸到红球的概率为 5 1 15 3p   ． 设“每位顾客获得 240 元返金券”为事件 A，则 3 3 3 1 1( ) C 3 27P A      ． 所以两位顾客均获得 240 元返金券的概率 1( ) ( ) 729P P A P A   ． （2）①若选择抽奖方案一，则每一次摸到红球的概率为 1 3 ，每一次摸到白球的概率为 2 3 ．设 获得返金券金额为 X 元，则 X 可能的取值为 60，120，180，240． 则 3 0 3 2( 60) C 3P X       8 27  ； 1 2 1 3 1 2 4( 120) C 3 3 9P X             ； 2 2 3 1 2 2( 180) C 3 3 9P X             ； 3 3 3 1( 240) C 3P X       1 27  ． 所以选择抽奖方案一，该顾客获得返金券金额的数学期望为 8( ) 60 12027E X     4 2 1180 240 1209 9 27      （元） 若选择抽奖方案二，设三次摸球的过程中，摸到红球的 次数为 Y，最终获得返金券的金额为 Z 元，则 1~ 3, 3Y B     ，故 1( ) 3 13E Y    ．所以选择抽 奖方案二，该顾客获得返金券金额的数学期望为 E(Z)＝E(100Y)＝100（元） ②即 E(X)＞E(Z)，所以应选择第一种抽奖方案． 20．【解】（1）由题意知 3 2 ce a   ，则 2 3 3a c ， 3 3b c ，∴ 22| | | | 2 bAB CD a a     4 3 3 53 3c c  ．所以 3c  ，所以椭圆的方程为 2 2 14 x y  ； （2）①当两条弦中一条斜率为 0 时，另一条弦的斜率不存在， 由题意知 1 | |2S AB 四边形 1| | 4 1 22CD     ． ②当两弦斜率均存在且不为 0 时，设 A(x1，y1)，B(x2，y2)， 且设直 线 AB 的方程为 ( 3)y k x  ， 则直线 CD 的方程为 1 ( 3)y xk    ． 将直线 AB 的方程 代入椭圆方程中，并整理得 2 2 2 2(1 4 8 3 12 4 0)k x k x k     ， 则 2 1 2 2 8 3 1 4 kx x k    ， 1 2x x  2 2 12 4 1 4 k k   所以 2 2 2 2 1 2 2 2 4 1 4(1| | 1 | 1 1 4 1 ) 4| k kAB k x x k k k          ， 同理| |CD  22 2 2 14 1 4(1 ) 4 41 kk k k        ， 所以 2 2 2 2 2 2 4 2 1 1 4(1 4(1 8(1| | | |2 2 1 4 4 4 1 ) ) 7 4 )k k kS AB CD k k k k            四边形 2 2 2 18 182 1 14 9 4 9 k k k kk k                    ， 由 221 14 9 4 2 9 25k kk k                ，当且仅当 k＝ ±1 时取等号．∴ 32 ,225S    四边形 ，综合①与②可知， 32 ,225S     四边形 ． 21．【解】 （1）∵ 1 01 x x   ．∴-1＜x＜1， 2 2( ) 1f x ax    ，∵-1＜x＜1，∴f′(x)≥ 2-a， （Ⅰ）当 a≤2 时，f′(x)≥0，∴f(x)在(-1，1)上单调递增； （Ⅱ）当 a＞2 时， ( ) 0f x  2 21 , 1x a a          ，∴f(x)在 2 21 , 1a a        上单调递减；∴f(x)在 21 1 a        ， 21 ,1a      上单调递增． （2）（Ⅰ）当 a≤2 时，由（1）知 f(x)在(-1，1)上单调递增；∴x∈(0，1)，f(x)＞f(0)＝0＞ f(-x)即有： 1ln1 x axx   ， 1ln1 x axx    ， 从而可得：1 1 axx ex   ，1 1 axx ex   ，∴ ax axe e  2 4 1 x x ； （Ⅱ）当 a＞2 时，由（1）知 f(x)在 2 21 , 1a a        上单调递减；∴ 20, 1x a       ， f(x)＜f(0)＝0＜f(-x)， 即有： 1ln1 x axx   ， 1ln1 x axx    从而可得：1 1 axx ex   ，1 1 axx ex   ， ∴ 2 4 1 ax ax xe e x    ，不合题意，舍去． 综上所述，实数 a 的取值范围为 a≤2． 22．【解】（1）由直线 l 的参数方程消去参数 t，得直线 l 的普通方程为 3 3 0x y   ， 又将曲线 C 的极坐标方程化为ρ2+3ρ2cos2θ＝4，曲线 C 的直角坐标方程为 2 2 14 yx   ． （2）将直线 l 的参数方程代入 2 2 14 yx   中，得 221 34 1 42 2t t             ，得 7t2+16t＝0 此 方程的两根为直线 l 与曲线 C 的交点 A，B 对应的参数 t1，t2，得 1 16 7t   ，t2＝0，∴由直线 参数的几何意义，知 1 2 16| | | | | || | 7AM BM t t    23．解：（1）∵f(x)＜|2x+1|-1，∴|x+1|-|2x+1|+1＜0 当 x＜-1 时，不等式可化为-x-1+(2x+1)+1 ＜0，解得 x＜-1，所以 x＜-1； 当 11 2x    ，不等式可化为 x+1+(2x+1)+1＜0，解得 x ＜-1，无解； 当 1 2x   时，不等式可化为 x+1-(2x+1)+1＜0，解得 x＞1，所以 x＞1 综上 所述，A＝(-∞，-1)∪(1，+∞) （2）因为 f(x-2)+f(x-3)＝|x-1|+|x-2|≥|(x-1)-(x-2)|＝1 且 f(x-2)+f(x-3)＜a 的解集不是空集， 所以 a＞1，即 a 的取值范围是(1，+∞)