- 4.47 MB
- 2021-06-16 发布
- 1、本文档由用户上传,淘文库整理发布,可阅读全部内容。
- 2、本文档内容版权归属内容提供方,所产生的收益全部归内容提供方所有。如果您对本文有版权争议,请立即联系网站客服。
- 3、本文档由用户上传,本站不保证质量和数量令人满意,可能有诸多瑕疵,付费之前,请仔细阅读内容确认后进行付费下载。
- 网站客服QQ:403074932
2006年普通高等学校招生全国统一考试(四川)韩先华编辑
数 学(理工农医类)
本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分。第Ⅰ卷 1至 2页。第Ⅱ卷 3到 8页。考试结束后,将本
试卷和答题卡一并交回。
第Ⅰ卷
注意事项:
1.答第Ⅰ卷前,考生务必将自己的姓名、准考证号、考试科目涂写在答题卡上。
2.每小题选出答案后,用铅笔把答题卡上对应题目的答案标号涂黑。如需改动,用橡皮擦干净后,再选涂其它答
案标号。不能答在试题卷上。
3.本卷共 12小题,每小题 5分,共 60分。在每小题给出的四个选项中,只有一项是符合题目要求的。
参考公式:
如果事件 A、B互斥,那么 球是表面积公式
)()()( BPAPBAP 24 RS
如果事件 A、B相互独立,那么 其中 R表示球的半径
)()()( BPAPBAP 球的体积公式
如果事件 A在一次试验中发生的概率是 P,那么
3
3
4 RV
n次独立重复试验中恰好发生 k次的概率 其中 R表示球的半径
knkk
nn PPCkP )1()(
一、选择题:本大题共 12 小题,每小题 5分,共 60 分。在每小题给出的四个选项中,只有一项是符合题目要求的。
1.已知集合 2A= | 5 6 0 , | 2 1 3 ,x x x B x x 则集合A B =
(A) | 2 3x x (B) | 2 3x x (C) | 2 3x x (D) | 1 3x x
2.复数 31 3i 的虚部为
(A)3. (B)-3. (C)2 (D)-2.
3. 已知
2 3, 1
( ) ,
2, 1
x x
f x
x
下面结论正确的是
(A)f(x)在 x=1 处连续 (B)f(1)=5 (C)
1
lim ( ) 2
x
f x
-
(D)
1
lim ( ) 5
x
f x
4. 已知二面角 l 的大小为
060 ,m n、 为异面直线, m n 且 , , m n则 、 所成的角为
(A) 030 (B) 060 (C) 090 (D) 0120
5. 下列函数中,图像的一部分如右图所示的是
(A) sin( )
6
y x
(B) sin(2 )
6
y x
(C) cos(4 )
3
y x
(D) cos(2 )
6
y x
6. 已知两定点 ( 2,0),A (1,0),B 如果动点 P 满足条件 2 ,PA PB 则点 P 的轨迹所包围的图形的面积等
于
(A) (B) 4 (C)8 (D)9
7.如图, 已知正六边形 1 2 3 4 5 6PP PP P P ,下列向量的数量积中最大的是
(A) 1 2 1 3PP PP
(B) 1 2 1 4PP PP
(C) 1 2 1 5PP PP
(D) 1 2 1 6PP PP
8. 某厂生产甲产品每千克需用原料 A 和原料 B 分别为 1 1a b、 千克,生产乙产品每千克需用原料 A和原料
B 分别为 2 2a b、 千克。甲、乙产品每千克可获利润分别为 1 2d d、 元。月初一次性购进本月用原料 A、B
各 1 2c c、 千克。要计划本月生产甲、乙两种产品各多少千克才能使月利润总额达到最大。在这个问题中,
设全月生产甲、乙两种产品分别为x千克、y千克,月利润总额为z元,那么,用于求使总利润
1 2z d x d y 最大的数学模型中,约束条件为
(A)
1 2 1
1 2 2
,
,
0,
0
a x a y c
b x b y c
x
y
(B)
1 1 1
2 2 2
,
,
0,
0
a x b y c
a x b y c
x
y
(C)
1 2 1
1 2 2
,
,
0,
0
a x a y c
b x b y c
x
y
(D)
1 2 1
1 2 2
,
,
0,
0
a x a y c
b x b y c
x
y
9. 直线y=x-3 与抛物线 xy 42 交于 A、B两点,过 A、B两点向抛物线的准线作垂线,垂足分别
为 P、Q ,则梯形 APQB的面积为
(A)48. (B)56 (C)64 (D)72.
10. 已知球 O 半径为 1,A、B、C 三点都在球面上,A、B 两点和 A、C 两点的球面距离都是
4
,B、C两点
的球面距离是
3
,则二面角B COA 的大小是
(A)
4
(B)
3
(C)
2
(D) 2
3
11. 设 cba 、、 分别为 ABC 的三内角 A B C、 、 所对的边,则
2 ( )a b b c 是 A B=2 的
(A)充要条件(B)充分而不必要条件(C)必要而不充分条件(D)既不充分也不必要条件 12. 从 0
到 9这 10个数字中任取 3个数字组成一个没有重复数字的三位数,这个数不能被3整除的概率为
(A) 19
54
(B) 35
54
(C) 38
54
(D) 41
60
第Ⅱ卷(非选择题 共 90 分)
二、填空题:本大题共 4小题,每小题 4分,共 16分。把答案填在题中横线上。
13.在三棱锥 O-ABC 中,三条棱 OA、OB、OC 两两互相垂直,且 OA=OB=OC,M 是 AB 的中点,则
OM与平面 ABC所成角的大小是______________(用反三角函数表示)。
14.设离散型随机变量ξ可能取的值为 1,2,3,4.P(ξ=k)=ak+b(k=1,2,3,4),又ξ的数学期望 Eξ=
3,则a+b=______________。
15.如图把椭圆
2 2
1
25 16
x y
的长轴 AB分成 8分,过每个分点作 x轴的
垂线交椭圆的上半部分于 1P , 2P ,…… 7P 七个点,F是椭圆的 一个焦
点,则 1 2 7......PF P F P F ____________.
16.非空集合 G 关于运算满足:(1)对任意的 , ,a b G 都有
,a b G (2)存在 ,e G 都有 ,a b b a a 则称 G关于运算为“融洽集”。现给出下列集合和
运算:
1 G={非负整数},为整数的加法。
2 G={偶数},为整数的乘法。
3 G={平面向量},为平面向量的加法。
4 G={二次三项式},为多项式的加法。
5 G={虚数},为复数的乘法。
其中 G关于运算为“融洽集”的是________。(写出所有“融洽集”的序号)
2006年普通高等学校招生全国统一考试(四川)韩先华编辑
数 学(理工农医类)
本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分。第Ⅰ卷 1至 2页。第Ⅱ卷 3到 8页。考试结束后,将本
试卷和答题卡一并交回。
第Ⅰ卷
一、选择题答题卡:
题号 1 2 3 4 5 6 7 8 9 10 11 12 得分
选项
二、填空题答题卡:
⒔ 。⒕ 。⒖ 。⒗ 。
三.解答题 共 6个小题,共 74分,解答时应写出必要的文字说明,证明过程或演算步骤.
17.(本小题满分 12分)
已知 A、B、C是 ABC 三内角,向量 ( 1, 3),m (cos ,sin ),n A A
且 1.m n
(Ⅰ)求角 A
(Ⅱ)若
2 2
1 sin 2 3,
cos sin
B
B B
求tanC。
18.(本小题满分 12分)
某课程考核分理论与实验两部分进行,每部分考核成绩只记“合格”与“不合格”,
两部分考核都“合格”则该课程考核“合格”。甲、乙、丙三人在理论考核中合
格的概率分别为 0.9、0.8、0.7;在实验考核中合格的概率分别为 0.8、0.7、0.9。所有考核是否合格相互
之间没有影响。
(Ⅰ)求甲、乙、丙三人在理论考核中至少有两人合格的概率;
(Ⅱ)求这三人该课程考核都合格的概率(结果保留三位小数)。
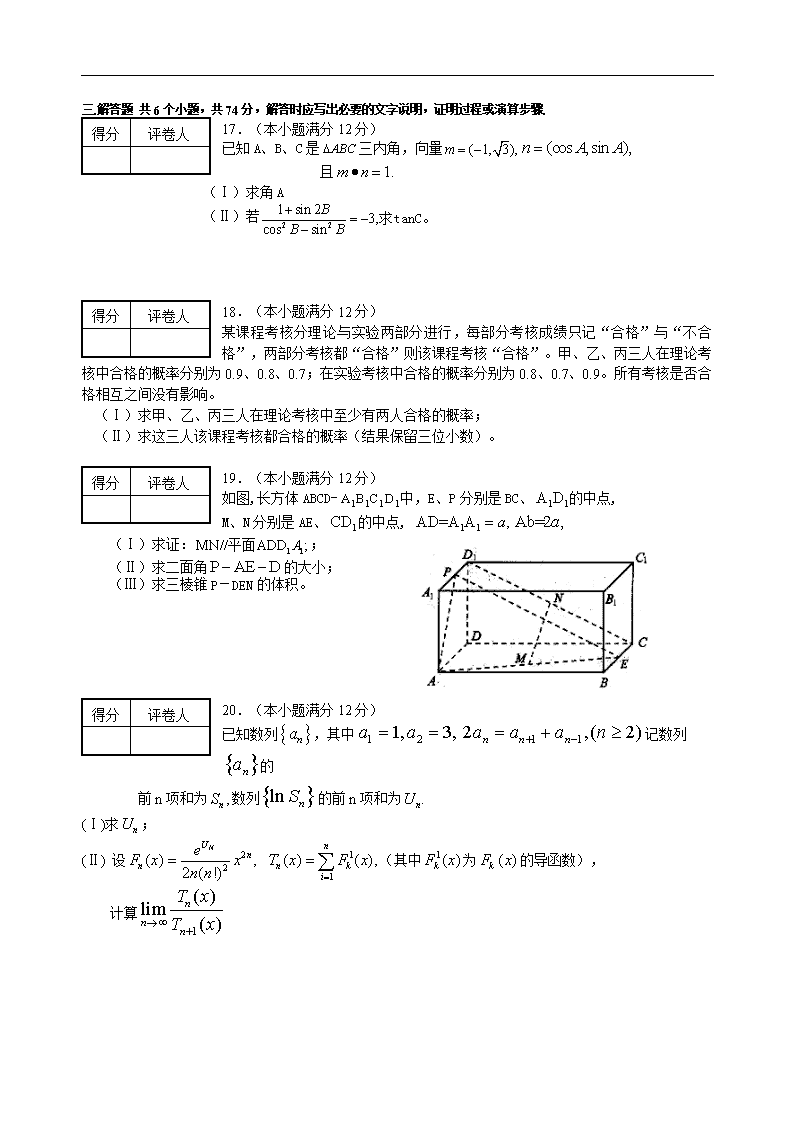
19.(本小题满分 12分)
如图,长方体 ABCD- 1111 DCBA 中,E、P 分别是 BC、 1 1A D 的中点,
M、N分别是 AE、 1CD 的中点, 1 1AD=A A ,a Ab=2 ,a
(Ⅰ)求证: 1 1MN// ADD ;A平面 ;
(Ⅱ)求二面角P AE D 的大小;
(Ⅲ)求三棱锥 P-DEN 的体积。
20.(本小题满分 12分)
已知数列 na ,其中 1 21, 3,a a 1 12 , ( 2)n n na a a n 记数列
na 的
前 n项和为 ,nS 数列 ln nS 的前 n项和为 .nU
(Ⅰ)求 nU ;
(Ⅱ) 设
2
2( ) ,
2 ( !)
NU
n
n
eF x x
n n
1
1
( ) ( ),
n
n k
i
T x F x
(其中
1( )kF x 为 ( )kF x 的导函数),
计算
1
( )lim
( )
n
n
n
T x
T x
得分 评卷人
得分 评卷人
得分 评卷人
得分 评卷人
21.(本小题满分 12分)
已知两定点 1( 2,0),F 2 ( 2,0),F 满足条件 2 1 2PF PF
的点 P 的轨迹是
曲线 E,直线y=kx-1 与曲线 E 交于 A、B 两点。如果 6 3,AB
且曲线 E
上存在点 C,使 ,OA OB mOC
求m ABC的值和 的面积S。
22.(本小题满分 14分)
已知函数
2 2f(x) + + ln ( 0),x a x x
x
f(x)的导函数是 f (x) 。对任意两个不
相等的正数 1 2x x、 ,证明:
(Ⅰ)当 0a 时, 1 2 1 2( ) ( ) ( )
2 2
f x f x x xf
;
(Ⅱ)当 4a 时, 1 2 1 2( ) ( )f x f x x x 。
2006年普通高等学校招生全国统一考试
(四川卷)理科数学及参考答案
本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分。第Ⅰ卷 1 至 2页。第Ⅱ卷 3 到 10 页。
考试结束后,将本试卷和答题卡一并交回。
第Ⅰ卷
注意事项:
1.答第Ⅰ卷前,考生务必将自己的姓名、准考证号、考试科目涂写在答题卡上。
2.每小题选出答案后,用铅笔把答题卡上对应题目的答案标号涂黑。如需改动,用橡皮擦干净后,
再选涂其它答案标号。不能答在试题卷上。
3.本卷共 12 小题,每小题 5分,共 60 分。在每小题给出的四个选项中,只有一项是符合题目要
求的。
参考公式:
如果事件 A、B互斥,那么 球是表面积公式
)()()( BPAPBAP 24 RS
如果事件 A、B相互独立,那么 其中 R表示球的半径
)()()( BPAPBAP 球的体积公式
如果事件 A在一次试验中发生的概率是 P,那么
3
3
4 RV
n次独立重复试验中恰好发生 k次的概率 其中 R表示球的半径
knkk
nn PPCkP )1()(
一.选择题:本大题共 12小题,每小题 5分,共 60分;
题号 1 2 3 4 5 6 7 8 9 10 11 12
答案 C D D B D B A C A C A B
(1)已知集合 2 5 6 0A x x x ,集合 2 1 3B x x ,则集合 A B
得分 评卷人
得分 评卷人
(A) 2 3x x (B) 2 3x x
(C) 2 3x x (D) 1 3x x
(2)复数的虚部为
(A)3 (B) 3 (C) 2 (D) 2
(3)已知
2 3, 1
2, 1
x x
f x
x
,下面结论正确的是
(A) f x 在 1x 处连续 (B) 5f x
(C)
1
lim 2
x
f x
(D)
1
lim 5
x
f x
(4)已知二面角 l 的大小为
060 , ,m n为异面直线,且 ,m n ,则 ,m n所成的角为
(A) 030 (B) 060 (C) 090 (D) 0120
(5)下列函数中,图象的一部分如右图所示的是
(A) sin
6
y x
(B) sin 2
6
y x
(C) cos 4
3
y x
(D) cos 2
6
y x
(6)已知两定点 2,0 , 1,0A B ,如果动点 P满足 2PA PB ,则点 P的轨迹所包围的图形的面
积等于
(A)9 (B)8 (C) 4 (D)
(7) 如图,已知正六边形 1 2 3 4 5 6PP PP P P ,下列向量的数量积中最大的是
(A) 1 2 1 3,PP PP
(B) 1 2 1 4,PP PP
(C) 1 2 1 5,PP PP
(D) 1 2 1 6,PP PP
(8) 某厂生产甲产品每千克需用原料 A和原料 B分别为 1 1,a b ,生产乙产品每千克需用原料 A和原料 B
分别为 2 2,a b 千克,甲、乙产品每千克可获利润分别为 1 2,d d 元,月初一次性够进本月用原料 ,A B各 1 2,c c
千克,要计划本月生产甲产品和乙产品各多少千克才能使月利润总额达到最大;在这个问题中,设全月
生产甲、乙两种产品分别为 x千克, y千克,月利润总额为 z元,那么,用于求使总利润 1 2z d x d y
最大的数学模型中,约束条件为
(A)
1 2 1
1 2 2
0
0
a x a y c
b x b y c
x
y
(B)
1 1 1
2 2 2
0
0
a x b y c
a x b y c
x
y
(C)
1 2 1
1 2 2
0
0
a x a y c
b x b y c
x
y
(D)
1 2 1
1 2 2
0
0
a x a y c
b x b y c
x
y
(9) 直线 3y x 与抛物线
2 4y x 交于 ,A B两点,过 ,A B两点向抛物线的准线作垂线,垂足分别为
,P Q,则梯形 APQB的面积为
(A) 48 (B)56 (C)64 (D)72
(10) 已知球O的半径是1, , ,A B C三点都在球面上, ,A B两点和 ,A C 两点的球面距离都是
4
, ,B C 两
点的球面距离是
3
,则二面角 B OA C 的大小是
(A)
4
(B)
3
(C)
2
(D)
2
3
(11)设 , ,a b c分别是 ABC 的三个内角 , ,A B C所对的边,则 2a b b c 是 2A B 的
(A)充分条件 (B)充分而不必要条件
(C)必要而充分条件 (D)既不充分又不必要条件
(12)从0到9这10个数字中任取3个数字组成一个没有重复数字的三位数,这个数不能被3整除的概
率为
(A)
41
60
(B)
38
54
(C)
35
54
(D)
19
54
第Ⅱ卷
二.填空题:本大题共 4小题,每小题 4分,共 16分;把答案填在题中的横线上。
(13)在三棱锥 0 ABC 中,三条棱 , ,OA OB OC 两两互相垂直,且 ,OA OB OC M 是 AB边的
中点,则OM 与平面 ABC所成角的大小是_____ arctan 2 ___________(用反三角函数表示)
(14)设离散性随机变量 可能取的值为 1,2,3,4, 1,2,3,4P k ak b k ,又 的数学期望
3E ,则 a b ______
1
10
__________;
(15)如图,把椭圆
2 2
1
25 16
x y
的长轴 AB分成8等份,过每个分点
作 x轴的垂线交椭圆的上半部分于 1 2 3 4 5 6 7, , , , , ,P P P P P P P 七个点, F 是椭圆的一个焦点,则
1 2 3 4 5 6 7PF P F PF P F P F P F P F _______35 _________;
(16)非空集合G关于运算满足:(1)对任意 ,a b G ,都有a b G ;
(2)存在 e G ,使得对一切 a G ,都有 a e e a a ,则称G 关于运算为“融洽集”;
现给出下列集合和运算:
① ,G 非负整数 为整数的加法 ② ,G 偶数 为整数的乘法
③ ,G 平面向量 为平面向量的加法 ④ ,G 二次三项式 为多项式的加法
⑤ ,G 虚数 为复数的乘法
其中G关于运算为“融洽集”______①,③__________;(写出所有“融洽集”的序号)
三.解答题:本大题共 6小题,共 74分;解答应写出文字说明,证明过程或演算步骤。
(17)(本大题满分 12分)
已知 , ,A B C是三角形 ABC 三内角,向量 1, 3 , cos ,sinm n A A
,且 1m n
(Ⅰ)求角 A;
(Ⅱ)若 2 2
1 sin 2 3
cos sin
B
B B
,求 tan B
本小题主要考察三角函数概念、同角三角函数的关系、两角和与差的三角函数的公式以及倍角
公式,考察应用、分析和计算能力。满分 12分。
解:(Ⅰ)∵ 1m n
∴ 1, 3 cos ,sin 1A A 即 3 sin cos 1A A
3 12 sin cos 1
2 2
A A
, 1sin
6 2
A
∵
50 ,
6 6 6
A A ∴
6 6
A
∴
3
A
(Ⅱ)由题知 2 2
1 2sin cos 3
cos sin
B B
B B
,整理得
2 2sin sin cos 2cos 0B B B B
∴ cos 0B ∴
2tan tan 2 0B B
∴ tan 2B 或 tan 1B
而 tan 1B 使
2 2cos sin 0B B ,舍去 ∴ tan 2B
∴ tan tanC A B tan A B
tan tan
1 tan tan
A B
A B
2 3
1 2 3
8 5 3
11
(18)(本大题满分 12分)
某课程考核分理论与实验两部分进行,每部分考核成绩只记“合格”与“不合格”,两部分考核
都是“合格”则该课程考核“合格”,甲、乙、丙三人在理论考核中合格的概率分别为0.9,0.8,0.7;在
实验考核中合格的概率分别为0.8,0.7,0.9,所有考核是否合格相互之间没有影响
(Ⅰ)求甲、乙、丙三人在理论考核中至少有两人合格的概率;
(Ⅱ)求这三人该课程考核都合格的概率。(结果保留三位小数)
本小题主要考察相互独立事件、互斥事件、对立事件等概率的计算方法,考察应用概率知识解
决实际问题的能力。满分 12分。
解:记“甲理论考核合格”为事件 1A;“乙理论考核合格”为事件 2A ;“丙理论考核合格”为事件 3A ;
记 iA 为 iA的对立事件, 1,2,3i ;记“甲实验考核合格”为事件 1B ;“乙实验考核合格”为事件 2B ;
“丙实验考核合格”为事件 3B ;
(Ⅰ)记“理论考核中至少有两人合格”为事件C,记C为C的对立事件
解法 1: 1 2 3 1 2 3 1 2 3 1 2 3P C P A A A A A A A A A A A A
1 2 3 1 2 3 1 2 3 1 2 3P A A A P A A A P A A A P A A A
0.9 0.8 0.3 0.9 0.2 0.7 0.1 0.8 0.7 0.9 0.8 0.7
0.902
解法 2: 1P C P C 1 2 3 1 2 3 1 2 3 1 2 31 P A A A A A A A A A A A A
1 2 3 1 2 3 1 2 3 1 2 31 P A A A P A A A P A A A P A A A
1 0.1 0.2 0.3 0.9 0.2 0.3 0.1 0.8 0.3 0.1 0.2 0.7
1 0.098 0.902
所以,理论考核中至少有两人合格的概率为0.902
(Ⅱ)记“三人该课程考核都合格” 为事件D
1 1 2 2 3 3P D P A B A B A B
1 1 2 2 3 3P A B P A B P A B
1 1 2 2 3 3P A P B P A P B P A P B
0.9 0.8 0.8 0.8 0.7 0.9
0.254016
0.254
所以,这三人该课程考核都合格的概率为0.254
(19)(本大题满分 12分)
如图,在长方体 1 1 1 1ABCD ABC D 中, ,E P分别是 1 1,BC AD 的
中点, ,M N 分别是 1,AE CD 的中点, 1 , 2AD AA a AB a
(Ⅰ)求证: //MN 面 1 1ADD A ;
(Ⅱ)求二面角 P AE D 的大小。
(Ⅲ)求三棱锥 P DEN 的体积。
本小题主要考察长方体的概念、直线和平面、平面和平面的关系等基础知识,以及空间想象能
力和推理能力。满分 12分
解法一:(Ⅰ)证明:取CD的中点K,连结 ,MK NK
∵ , ,M N K 分别为 1, ,AK CD CD的中点
∵ 1// , //MK AD NK DD
∴ //MK 面 1 1ADD A , //NK 面 1 1ADD A
∴面 //MNK 面 1 1ADD A ∴ //MN 面 1 1ADD A
(Ⅱ)设 F 为 AD的中点
∵ P为 1 1AD 的中点 ∴ 1//PF D D ∴PF 面 ABCD
作 FH AE ,交 AE于H ,连结PH ,则由三垂线定理得 AE PH
从而 PHF 为二面角 P AE D 的平面角。
在 Rt AEF 中,
17, 2 ,
2 2
aAF EF a AE a ,从而
2 22
17 17
2
a aAF EF aFH
AE
a
在 Rt PFH 中, 1 17tan
2
DDPFPFH
FH FH
故:二面角 P AE D 的大小为 17arctan
2
(Ⅲ)
1
2 2 2
1
1 1 1 54
2 4 4 4NEP ECD PS S BC CD a a a a 矩形
作 1DQ CD ,交 1CD 于Q,由 1 1AD 面 1 1CDDC 得 1 1AC DQ
∴DQ 面 1 1BCD A
∴在 1Rt CDD 中, 1
1
2 2
5 5
CD DD a aDQ a
CD a
∴
1
3P DEN D ENP NEPV V S DQ 21 5 2
3 4 5
a a 31
6
a
方法二:以D为原点, 1, ,DA DC DD 所在直线分别为 x轴, y轴, z轴,建立直角坐标系,则
1 1,0,0 , , 2 ,0 , 0, 2 ,0 , ,0, , 0,0,A a B a a C a A a a D a
∵ , , ,E P M N 分别是 1 1 1, , ,BC AD AE CD 的中点
∴
3, 2 ,0 , , 0, , , , 0 , 0, , ,
2 2 4 2
a a a aE a P a M a N a
(Ⅰ)
3 ,0,
4 2
aMN a
取 0,1,0n
,显然 n
面 1 1ADD A
0MN n
,∴MN n
又MN 面 1 1ADD A ∴ //MN 面 1 1ADD A
(Ⅱ)过 P作 PH AE ,交 AE于H ,取 AD的中点F ,则 ,0,0
2
aF
∵
设 , ,0H x y ,则 , , , , ,0
2 2
a aHP x y a HF x y
又 , 2 ,0
2
aAE a
由 0AP AE
,及H 在直线 AE上,可得:
2
2 0
4 2
4 4
a a x ay
x y a
解得
33 2,
34 17
x a y a
∴
8 2 8 2, , , , ,0
17 17 17 17
a a a aHP a HF
∴ 0HF AE
即HF AE
∴HP
与HF
所夹的角等于二面角 P AE D 的大小
2cos ,
21
HP HFHP HF
HP HF
故:二面角 P AE D 的大小为
2 21arccos
21
(Ⅲ)设 1 1 1 1, ,n x y z
为平面DEN的法向量,则 1 1,n DE n DN
又 , 2 ,0 , 0, , , , 0,
2 2 2
a a aDE a DN a DP a
∴
1 1
1 1
2 0
2
2 0
2
a x ay
ay z
即
1 1
1 1
4
2
x y
z y
∴可取 1 4, 1,2n
∴P点到平面DEN的距离为
1
1
2 2 4
16 1 4 21
DP n a a ad
n
∵
8cos ,
85
DE DNDE DN
DE DN
,
21sin ,
85
DE DN
∴
21 21sin ,
2 8DENS DE DN DE DN a
∴
3
21 1 21 4
3 3 8 621P DEN DEN
a aV S d a
(20)(本大题满分 12分)
已知数列 na ,其中 1 2 1 11, 3,2 2n n na a a a a n ,记数列 na 的前 n项和为 nS ,数
列 ln nS 的前 n项和为 nU
(Ⅰ)求 nU ;
(Ⅱ)设
2 '
2
1
0 ,
2 !
nU n
n
n n k
k
eF x x x T x F x
n n
,(其中 '
kF x 为 kF x 的导函数),计
算
1
lim n
n
n
T x
T x
本小题主要考察等差数列、等比数列的基础知识,以及对数运算、导数运算和极限运算的能力,
同时考查分类讨论的思想方法,满分 12分。
解:(Ⅰ)由题意, na 是首项为1,公差为 2的等差数列
前n项和
21 1 2 1
2n
n
S n n
,
2ln ln 2lnnS n n
2 ln1 ln 2 ln 2ln !nU n n
(Ⅱ)
2 2
2 2
2 2
!
22 ! 2 !
nU n
n n
n
ne xF x x x
nn n n n
' 2 1n
nF x x
2
2
' 2 1
1 1 2
2
1
0 1
1
1
1
1
1
n
n n
k
n k
k k n
x x
x
x
T x F x x n x
x x
x
x
2
2 2
1
2
2
2
1lim 1 0 1
1
lim lim 1 1
1
1 1
lim 1
1
n
nn
n
n n
n
n
n
n
x x
x
T x n x
T x n
x x
x
x
(21)(本大题满分 14分)
已知两定点 1 22,0 , 2,0F F ,满足条件 2 1 2PF PF
的点 P的轨迹是曲线 E,直线
1y kx 与曲线 E交于 ,A B两点,如果 6 3AB ,且曲线 E上存在点C,使OA OB mOC
,
求m的值和 ABC 的面积 S
本小题主要考察双曲线的定义和性质、直线与双曲线的关系、点到直线的距离等知识及解析几
何的基本思想、方法和综合解决问题的能力。满分 12分。
解:由双曲线的定义可知,曲线 E是以 1 22,0 , 2,0F F 为焦点的双曲线的左支,
且 2, 1c a ,易知 1b
故曲线E的方程为 2 2 1 0x y x
设 1 1 2 2, , ,A x y B x y ,由题意建立方程组 2 2
1
1
y kx
x y
消去 y ,得 2 21 2 2 0k x kx
又已知直线与双曲线左支交于两点 ,A B,有
2
2 2
1 2 2
1 2 2
1 0
2 8 1 0
2 0
1
2 0
1
k
k k
kx x
k
x x
k
解得 2 1k
又∵
2
1 21AB k x x 22
1 2 1 21 4k x x x x
2
2
2 2
2 21 4
1 1
kk
k k
2 2
22
1 2
2
1
k k
k
依题意得
2 2
22
1 2
2 6 3
1
k k
k
整理后得 4 228 55 25 0k k
∴ 2 5
7
k 或 2 5
4
k 但 2 1k ∴
5
2
k
故直线 AB的方程为
5 1 0
2
x y
设 ,c cC x y ,由已知OA OB mOC
,得 1 1 2 2, , ,c cx y x y mx my
∴ 1 2 1 2, ,c c
x x y ymx my
m m
, 0m
又 1 2 2
2 4 5
1
kx x
k
,
2
1 2 1 2 2 2
2 22 2 8
1 1
ky y k x x
k k
∴点 4 5 8,C
m m
将点C的坐标代入曲线 E的方程,得 2 2
80 64 1
m m
得 4m ,但当 4m 时,所得的点在双曲线的右支上,不合题意
∴ 4m ,C点的坐标为 5,2
C到 AB的距离为
2
2
5 5 2 1
2 1
35 1
2
∴ ABC 的面积
1 16 3 3
2 3
S
(22)(本大题满分 14分)
已知函数 2 2 ln 0f x x a x x
x
, f x 的导函数是 'f x ,对任意两个不相等的正
数 1 2,x x ,证明:
(Ⅰ)当 0a 时,
1 2 1 2
2 2
f x f x x xf
(Ⅱ)当 4a 时, ' '
1 2 1 2f x f x x x
本小题主要考查导数的基本性质和应用,函数的性质和平均值不等式等知识及综合分析、推
理论证的能力,满分 14分。
证明:(Ⅰ)由 2 2 lnf x x a x
x
得
1 2 2 2
1 2 1 2
1 2
1 1 1 ln ln
2 2 2
f x f x ax x x x
x x
2 2 1 2
1 2 1 2
1 2
1 ln
2
x xx x a x x
x x
2
1 2 1 2 1 2
1 2
4 ln
2 2 2
x x x x x xf a
x x
而
2
22 2 2 2 1 2
1 2 1 2 1 2
1 1 2
2 4 2
x xx x x x x x
①
又 2 2 2
1 2 1 2 1 2 1 22 4x x x x x x x x
∴ 1 2
1 2 1 2
4x x
x x x x
②
∵ 1 2
1 2 2
x xx x
∴ 1 2
1 2ln ln
2
x xx x
∵ 0a ∴ 1 2
1 2ln ln
2
x xa x x a
③
由①、②、③得
2
2 2 1 2 1 2
1 2 1 2 1 2
1 2 1 2
1 4ln ln
2 2
x x x xx x a x x a x x
x x x x
即
1 2 1 2
2 2
f x f x x xf
(Ⅱ)证法一:由 2 2 lnf x x a x
x
,得 '
2
22 af x x
x x
∴ ' '
1 2 1 22 2
1 1 2 2
2 22 2a af x f x x x
x x x x
1 2
1 2 2 2
1 2 1 2
2
2
x x ax x
x x x x
1 2' '
1 2 1 2 2 2
1 2 1 2
2
2 1
x x af x f x x x
x x x x
下面证明对任意两个不相等的正数 1 2,x x ,有
1 2
2 2
1 2 1 2
2
2 1
x x a
x x x x
恒成立
即证
1 2
1 2
1 2
2 x x
a x x
x x
成立
∵
1 2
1 2 1 2
1 2 1 2
2 4x x
x x x x
x x x x
设 2
1 2
4, 0t x x u x t t
t
,则 '
2
42u x t
t
令 ' 0u x 得 3 2t ,列表如下:
t 30, 2 3 2 3 2,
'u t _ 0
u t 极小值 33 4
3 33 4 108 4u t a ∴
1 2
1 2
1 2
2 x x
x x a
x x
∴对任意两个不相等的正数 1 2,x x ,恒有 ' '
1 2 1 2f x f x x x
证法二:由 2 2 lnf x x a x
x
,得 '
2
22 af x x
x x
∴ ' '
1 2 1 22 2
1 1 2 2
2 22 2a af x f x x x
x x x x
1 2
1 2 2 2
1 2 1 2
2
2
x x ax x
x x x x
∵ 1 2,x x 是两个不相等的正数
∴
1 2
32 2
1 2 1 2 1 21 2
2 42 2
x x a a
x x x x x xx x
3 1 21 2
4 42
x xx x
设
1 2
1t
x x
, 3 22 4 4 0u t t t t
则 ' 4 3 2u t t t ,列表:
t
20,
3
2
3
2 ,
3
'u t _ 0
u t 极小值
38
27
∴
38 1
27
u 即
1 2
2 2
1 2 1 2
2
2 1
x x a
x x x x
∴ 1 2' '
1 2 1 2 1 22 2
1 2 1 2
2
2
x x af x f x x x x x
x x x x
即对任意两个不相等的正数 1 2,x x ,恒有 ' '
1 2 1 2f x f x x x
录入:四川省内江市隆昌县黄家中学
程 亮
lc_chengliang@163.com
参考答案
一.选择题:
题号 1 2 3 4 5 6 7 8 9 10 11 12
答案 C D D B D B A C A C A B
(1)已知集合 2 5 6 0A x x x ={ | 2 3}x x≤ ≤ ,集合 2 1 3B x x { | 2或 1}x x x ,
则集合 A B 2 3x x ,选 C.
(2)复数 31 i =1 3 3 2 2i i i ,所以它的虚部为-2,选 D.
(3)已知
2 3, 1
2, 1
x x
f x
x
,则
1 1
lim ( ) lim ( ) 5
x x
f x f x
,而 (1) 2f ,∴ 正确的结论是
1
lim 5
x
f x
,选 D.
(4)已知二面角 l 的大小为
060 , ,m n为异面直线,且 ,m n ,则 ,m n所成的角为两条
直线所成的角,∴ θ= 060 ,选 B.
(5)从图象看出,
4
1
T=
12 6 4
,所以函数的最小正周期为π,函数应
为 y= sin 2x向左平移了
6
个单位,
即 sin 2( )
6
y x
= sin(2 ) cos( 2 ) cos(2 )
3 2 3 6
x x x
,所
以选 D.
(6)已知两定点 2,0 , 1,0A B ,如果动点 P满足 2PA PB ,设 P点的坐标为(x,y),
则
2 2 2 2( 2) 4[( 1) ]x y x y ,即
2 2( 2) 4x y ,所以点 P的轨迹
所包围的图形的面积等于 4π,选 B.
(7) 如图,已知正六边形 1 2 3 4 5 6PP PP P P ,设边长 1 2| |PP a ,则∠ 2 1 3P PP =
6
.,
1 3| | 3PP a , 1 2 1 3,PP PP
=
23 33
2 2
aa a ,∠ 2 1 4P PP =
3
, 1 4| | 2PP a ,
1 2 1 4,PP PP
= 212
2
a a a , 1 2 1 5,PP PP
=0, 1 2 1 6,PP PP
<0,∴ 数量积中最大的是 1 2 1 3,PP PP
,选 A.
(8) 某厂生产甲产品每千克需用原料 A和原料 B分别为 1 1,a b ,生产乙产品每千克需用原料 A和原料 B
分别为 2 2,a b 千克,甲、乙产品每千克可获利润分别为 1 2,d d
元,月初一次性够进本月用原料 ,A B各 1 2,c c 千克,要计划
本月生产甲产品和乙产品各多少千克才能使月利润总额达
到最大;在这个问题中,设全月生产甲、乙两种产品分别
为 x千克, y千克,月利润总额为 z 元,那么,用于求使
总利润 1 2z d x d y 最大的数学模型中,约束条件为
1 2 1
1 2 2
0
0
a x a y c
b x b y c
x
y
,选 C.
(9) 直线 3y x 与抛物线
2 4y x 交于 ,A B两点,过 ,A B两点向抛物线的准线作垂线,垂足分别为
,P Q,联立方程组得
2 4
3
y x
y x
,消元得
2 10 9 0x x ,解得
1
2
x
y
,和
9
6
x
y
,∴ |AP|=10,
|BQ|=2,|PQ|=8,梯形 APQB的面积为 48,选 A.
(10) 已知球O的半径是 R=1, , ,A B C三点都在球面上, ,A B两点和 ,A C 两点的球面距离都是
4
,则
∠AOB,∠AOC都等于
4
,AB=AC, ,B C 两点的球面距离是
3
,∠BOC=
3
,BC=1,过 B做 BD⊥
AO,垂足为 D,连接 CD,则 CD⊥AD,则∠BDC是二面角 B OA C 的平面角,BD=CD=
2
2
,∴
∠BDC=
2
,二面角 B OA C 的大小是
2
,选 C.
(11)设 , ,a b c分别是 ABC 的三个内角 , ,A B C所对的边,若 2a b b c ,
则
2sin sin (sin sin )A B B C ,则
1 cos 2 1 cos 2 sin sin
2 2
a B B C
,
∴
1 (cos 2 cos 2 ) sin sin
2
B A B C , sin( )sin( ) sin sinB A A B B C ,
又 sin( ) sinA B C ,∴ sin( ) sinA B B ,∴ A B B , 2A B ,
若△ABC中, 2A B ,由上可知,每一步都可以逆推回去,得到 2a b b c ,
所以 2a b b c 是 2A B 的充要条件,选 A.
(12)从 0到9这10个数字中任取3个数字组成一个没有重复数字的三位数,这个数不能被3整除。
所有的三位数有
3 2
10 9 648A A 个,将 10个数字分成三组,即被 3 除余 1的有{1,4,7}、被 3除
余 2的有{2,5,8},被 3整除的有{3,6,9,0},若要求所得的三位数被 3整除,则可以分类讨论:
①三个数字均取第一组,或均取第二组,有
3
32 12A 个;② 若三个数字均取自第三组,则要考虑
取出的数字中有无数字 0,共有
3 2
4 3 18A A 个;③ 若三组各取一个数字,第三组中不取 0,有
1 1 1 3
3 3 3 3 162C C C A 个,④若三组各取一个数字,第三组中取 0,有
1 1 2
3 3 22 36C C A 个,这样
能被 3 整除的数共有 228个,不能被3整除的数有 420个,所以概率为
420
648
=
35
54
,选 B。
二填空题:
(13)在三棱锥O ABC 中,三条棱 , ,OA OB OC 两两互相垂直,且
,OA OB OC M 是 AB 边 的 中 点 , 设 | |OA a , 则
| | | | | | 2AB BC CA a ,
31
6O ABCV a ,O 点在底面的射影为底面△
ABC的中心,| | 1
3
O ABC
ABC
VOD
S
=
3
3
a,又
1 3| | | |
3 6
DM MC a ,OM
D
M
C
BA
O
与平面 ABC所成角的正切是
3
3tan 2
6
6
,所以二面角大小是 arctan 2 .
(14)设离散性随机变量 可能取的值为 1,2,3,4, 1,2,3,4P k ak b k ,所以
( ) (2 ) (3 ) (4 ) 1a b a b a b a b ,即10 4 1a b ,又 的数学期望 3E ,则
( ) 2(2 ) 3(3 ) 4(4 ) 3a b a b a b a b ,即30 10 3a b ,
1 , 0
10
a b ,∴ a b
1
10
.
(15)如图,把椭圆
2 2
1
25 16
x y
的长轴 AB分成8等份,过每个分点作
x轴的垂线交椭圆的上半部分于 1 2 3 4 5 6 7, , , , , ,P P P P P P P 七个点, F 是椭圆
的 一 个 焦 点 , 则 根 据 椭 圆 的 对 称 性 知 ,
1 1 7 1 1 1 1 2| | | | | | | | 2PF P F PF PF a ,同理其余两对的和也是 2a ,又
4 1| |P F a ,∴ 1 2 3 4 5 6 7PF P F PF P F P F P F P F 7a =35
(16)非空集合G关于运算满足:(1)对任意 ,a b G ,都有a b G ;
(2)存在 e G ,使得对一切 a G ,都有 a e e a a ,则称G 关于运算为“融洽集”;
现给出下列集合和运算:
① ,G 非负整数 为整数的加法 , 满 足 任 意 ,a b G , 都 有 a b G , 且 令 0e , 有
0 0a a a ,所以①符合要求;
② ,G 偶数 为整数的乘法 ,若存在 a e a e a ,则 1e ,矛盾,∴ ②不符合要求;
③ ,G 平面向量 为平面向量的加法,取 0e
,满足要求,∴ ③符合要求;
④ ,G 二次三项式 为多项式的加法,两个二次三项式相加得到的可能不是二次三项式,所以④
不符合要求;
⑤ ,G 虚数 为复数的乘法,两个虚数相乘得到的可能是实数,∴ ⑤不符合要求,
这样G关于运算为“融洽集”的有①③。
三.解答题:
17.本小题主要考察三角函数概念、同角三角函数的关系、两角和与差的三角函数的公式以及倍角公
式,考察应用、分析和计算能力。满分 12分。
解:(Ⅰ)∵ 1m n
∴ 1, 3 cos ,sin 1A A 即 3 sin cos 1A A
3 12 sin cos 1
2 2
A A
, 1sin
6 2
A
∵
50 ,
6 6 6
A A ∴
6 6
A
∴
3
A
(Ⅱ)由题知 2 2
1 2sin cos 3
cos sin
B B
B B
,整理得
2 2sin sin cos 2cos 0B B B B
∴ cos 0B ∴
2tan tan 2 0B B
∴ tan 2B 或 tan 1B
而 tan 1B 使
2 2cos sin 0B B ,舍去 ∴ tan 2B
∴ tan tanC A B tan A B
tan tan
1 tan tan
A B
A B
2 3
1 2 3
8 5 3
11
18.本小题主要考察相互独立事件、互斥事件、对立事件等概率的计算方法,考察应用概率知识解决
实际问题的能力。满分 12分。
解:记“甲理论考核合格”为事件 1A;“乙理论考核合格”为事件 2A ;“丙理论考核合格”为事件 3A ;
记 iA 为 iA的对立事件, 1,2,3i ;记“甲实验考核合格”为事件 1B ;“乙实验考核合格”为事件 2B ;
“丙实验考核合格”为事件 3B ;
(Ⅰ)记“理论考核中至少有两人合格”为事件C,记C为C的对立事件
解法 1: 1 2 3 1 2 3 1 2 3 1 2 3P C P A A A A A A A A A A A A
1 2 3 1 2 3 1 2 3 1 2 3P A A A P A A A P A A A P A A A
0.9 0.8 0.3 0.9 0.2 0.7 0.1 0.8 0.7 0.9 0.8 0.7
0.902
解法 2: 1P C P C 1 2 3 1 2 3 1 2 3 1 2 31 P A A A A A A A A A A A A
1 2 3 1 2 3 1 2 3 1 2 31 P A A A P A A A P A A A P A A A
1 0.1 0.2 0.3 0.9 0.2 0.3 0.1 0.8 0.3 0.1 0.2 0.7
1 0.098 0.902
所以,理论考核中至少有两人合格的概率为0.902
(Ⅱ)记“三人该课程考核都合格” 为事件D
1 1 2 2 3 3P D P A B A B A B
1 1 2 2 3 3P A B P A B P A B
1 1 2 2 3 3P A P B P A P B P A P B
0.9 0.8 0.8 0.8 0.7 0.9
0.254016
0.254
所以,这三人该课程考核都合格的概率为0.254
19.本小题主要考察长方体的概念、直线和平面、平面和平面的关系等基础知识,以及空间想象能力
和推理能力。满分 12分
解法一:(Ⅰ)证明:取CD的中点K,连结 ,MK NK
∵ , ,M N K 分别为 1, ,AK CD CD的中点
∵ 1// , //MK AD NK DD
∴ //MK 面 1 1ADD A , //NK 面 1 1ADD A
∴面 //MNK 面 1 1ADD A ∴ //MN 面 1 1ADD A
(Ⅱ)设 F 为 AD的中点
∵ P为 1 1AD 的中点 ∴ 1//PF D D ∴PF 面 ABCD
作 FH AE ,交 AE于H ,连结PH ,则由三垂线定理得 AE PH
从而 PHF 为二面角 P AE D 的平面角。
在 Rt AEF 中,
17, 2 ,
2 2
aAF EF a AE a ,从而
2 22
17 17
2
a aAF EF aFH
AE
a
在 Rt PFH 中, 1 17tan
2
DDPFPFH
FH FH
故:二面角 P AE D 的大小为
17arctan
2
(Ⅲ)
1
2 2 2
1
1 1 1 54
2 4 4 4NEP ECD PS S BC CD a a a a 矩形
作 1DQ CD ,交 1CD 于Q,由 1 1AD 面 1 1CDDC 得 1 1AC DQ
∴DQ 面 1 1BCD A
∴在 1Rt CDD 中, 1
1
2 2
5 5
CD DD a aDQ a
CD a
∴
1
3P DEN D ENP NEPV V S DQ 21 5 2
3 4 5
a a 31
6
a
方法二:以D为原点, 1, ,DA DC DD 所在直线分别为 x轴, y轴, z轴,建立直角坐标系,则
1 1,0,0 , , 2 ,0 , 0, 2 ,0 , ,0, , 0,0,A a B a a C a A a a D a
∵ , , ,E P M N 分别是 1 1 1, , ,BC AD AE CD 的中点
∴
3, 2 ,0 , , 0, , , , 0 , 0, , ,
2 2 4 2
a a a aE a P a M a N a
(Ⅰ)
3 ,0,
4 2
aMN a
取 0,1,0n
,显然 n
面 1 1ADD A
0MN n
,∴MN n
又MN 面 1 1ADD A ∴ //MN 面 1 1ADD A
(Ⅱ)过 P作 PH AE ,交 AE于H ,取 AD的中点F ,则 ,0,0
2
aF
∵
设 , ,0H x y ,则 , , , , ,0
2 2
a aHP x y a HF x y
又 , 2 ,0
2
aAE a
由 0AP AE
,及H 在直线 AE上,可得:
2
2 0
4 2
4 4
a a x ay
x y a
解得
33 2,
34 17
x a y a
∴
8 2 8 2, , , , ,0
17 17 17 17
a a a aHP a HF
∴ 0HF AE
即HF AE
∴HP
与HF
所夹的角等于二面角 P AE D 的大小
2cos ,
21
HP HFHP HF
HP HF
故:二面角 P AE D 的大小为
2 21arccos
21
(Ⅲ)设 1 1 1 1, ,n x y z
为平面DEN的法向量,则 1 1,n DE n DN
又 , 2 ,0 , 0, , , , 0,
2 2 2
a a aDE a DN a DP a
∴
1 1
1 1
2 0
2
2 0
2
a x ay
ay z
即
1 1
1 1
4
2
x y
z y
∴可取 1 4, 1,2n
∴P点到平面DEN的距离为
1
1
2 2 4
16 1 4 21
DP n a a ad
n
∵
8cos ,
85
DE DNDE DN
DE DN
,
21sin ,
85
DE DN
∴
21 21sin ,
2 8DENS DE DN DE DN a
∴
3
21 1 21 4
3 3 8 621P DEN DEN
a aV S d a
20.本小题主要考察等差数列、等比数列的基础知识,以及对数运算、导数运算和极限运算的能力,同
时考查分类讨论的思想方法,满分 12分。
解:(Ⅰ)由题意, na 是首项为1,公差为 2的等差数列
前n项和
21 1 2 1
2n
n
S n n
,
2ln ln 2lnnS n n
2 ln1 ln 2 ln 2ln !nU n n
(Ⅱ)
2 2
2 2
2 2
!
22 ! 2 !
nU n
n n
n
ne xF x x x
nn n n n
' 2 1n
nF x x
2
2
' 2 1
1 1 2
2
1
0 1
1
1
1
1
1
n
n n
k
n k
k k n
x x
x
x
T x F x x n x
x x
x
x
2
2 2
1
2
2
2
1lim 1 0 1
1
lim lim 1 1
1
1 1
lim 1
1
n
nn
n
n n
n
n
n
n
x x
x
T x n x
T x n
x x
x
x
21.本小题主要考察双曲线的定义和性质、直线与双曲线的关系、点到直线的距离等知识及解析几何的
基本思想、方法和综合解决问题的能力。满分 12分。
解:由双曲线的定义可知,曲线 E是以 1 22,0 , 2,0F F 为焦点的双曲线的左支,
且 2, 1c a ,易知 1b
故曲线E的方程为 2 2 1 0x y x
设 1 1 2 2, , ,A x y B x y ,由题意建立方程组 2 2
1
1
y kx
x y
消去 y ,得 2 21 2 2 0k x kx
又已知直线与双曲线左支交于两点 ,A B,有
2
2 2
1 2 2
1 2 2
1 0
2 8 1 0
2 0
1
2 0
1
k
k k
kx x
k
x x
k
解得 2 1k
又∵
2
1 21AB k x x 22
1 2 1 21 4k x x x x
2
2
2 2
2 21 4
1 1
kk
k k
2 2
22
1 2
2
1
k k
k
依题意得
2 2
22
1 2
2 6 3
1
k k
k
整理后得 4 228 55 25 0k k
∴ 2 5
7
k 或 2 5
4
k 但 2 1k ∴
5
2
k
故直线 AB的方程为
5 1 0
2
x y
设 ,c cC x y ,由已知OA OB mOC
,得 1 1 2 2, , ,c cx y x y mx my
∴ 1 2 1 2, ,c c
x x y ymx my
m m
, 0m
又 1 2 2
2 4 5
1
kx x
k
,
2
1 2 1 2 2 2
2 22 2 8
1 1
ky y k x x
k k
∴点 4 5 8,C
m m
将点C的坐标代入曲线 E的方程,得 2 2
80 64 1
m m
得 4m ,但当 4m 时,所得的点在双曲线的右支上,不合题意
∴ 4m ,C点的坐标为 5,2
C到 AB的距离为
2
2
5 5 2 1
2 1
35 1
2
∴ ABC 的面积
1 16 3 3
2 3
S
22.本小题主要考查导数的基本性质和应用,函数的性质和平均值不等式等知识及综合分析、推理论证
的能力,满分 14分。
证明:(Ⅰ)由 2 2 lnf x x a x
x
得
1 2 2 2
1 2 1 2
1 2
1 1 1 ln ln
2 2 2
f x f x ax x x x
x x
2 2 1 2
1 2 1 2
1 2
1 ln
2
x xx x a x x
x x
2
1 2 1 2 1 2
1 2
4 ln
2 2 2
x x x x x xf a
x x
而
2
22 2 2 2 1 2
1 2 1 2 1 2
1 1 2
2 4 2
x xx x x x x x
①
又 2 2 2
1 2 1 2 1 2 1 22 4x x x x x x x x
∴ 1 2
1 2 1 2
4x x
x x x x
②
∵ 1 2
1 2 2
x xx x
∴ 1 2
1 2ln ln
2
x xx x
∵ 0a ∴ 1 2
1 2ln ln
2
x xa x x a
③
由①、②、③得
2
2 2 1 2 1 2
1 2 1 2 1 2
1 2 1 2
1 4ln ln
2 2
x x x xx x a x x a x x
x x x x
即
1 2 1 2
2 2
f x f x x xf
(Ⅱ)证法一:由 2 2 lnf x x a x
x
,得 '
2
22 af x x
x x
∴ ' '
1 2 1 22 2
1 1 2 2
2 22 2a af x f x x x
x x x x
1 2
1 2 2 2
1 2 1 2
2
2
x x ax x
x x x x
1 2' '
1 2 1 2 2 2
1 2 1 2
2
2 1
x x af x f x x x
x x x x
下面证明对任意两个不相等的正数 1 2,x x ,有
1 2
2 2
1 2 1 2
2
2 1
x x a
x x x x
恒成立
即证
1 2
1 2
1 2
2 x x
a x x
x x
成立
∵
1 2
1 2 1 2
1 2 1 2
2 4x x
x x x x
x x x x
设 2
1 2
4, 0t x x u x t t
t
,则 '
2
42u x t
t
令 ' 0u x 得 3 2t ,列表如下:
t 30, 2 3 2 3 2,
'u t _ 0
u t 极小值 33 4
3 33 4 108 4u t a ∴
1 2
1 2
1 2
2 x x
x x a
x x
∴对任意两个不相等的正数 1 2,x x ,恒有 ' '
1 2 1 2f x f x x x
证法二:由 2 2 lnf x x a x
x
,得 '
2
22 af x x
x x
∴ ' '
1 2 1 22 2
1 1 2 2
2 22 2a af x f x x x
x x x x
1 2
1 2 2 2
1 2 1 2
2
2
x x ax x
x x x x
∵ 1 2,x x 是两个不相等的正数
∴
1 2
32 2
1 2 1 2 1 21 2
2 42 2
x x a a
x x x x x xx x
3 1 21 2
4 42
x xx x
设
1 2
1t
x x
, 3 22 4 4 0u t t t t
则 ' 4 3 2u t t t ,列表:
t 20,
3
2
3
2 ,
3
'u t _ 0
u t 极小值
38
27
∴
38 1
27
u 即
1 2
2 2
1 2 1 2
2
2 1
x x a
x x x x
∴ 1 2' '
1 2 1 2 1 22 2
1 2 1 2
2
2
x x af x f x x x x x
x x x x
即对任意两个不相等的正数 1 2,x x ,恒有 ' '
1 2 1 2f x f x x x
相关文档
- 【数学】2020届北京一轮复习通用版2021-06-165页
- 【数学】2020届一轮复习人教版(理)第2021-06-1614页
- 【数学】2020届一轮复习苏教版任意2021-06-1614页
- 【数学】2020届一轮复习人教A版第32021-06-164页
- 【数学】2020届一轮复习北师大版坐2021-06-164页
- 【数学】2020届一轮复习人教B版18-2021-06-164页
- 2021届高考数学一轮复习第八章立体2021-06-1617页
- 辽宁省锦州市2020届高三4月质量检2021-06-1621页
- 【数学】2018届一轮复习人教A版9-62021-06-1618页
- 【数学】2018届一轮复习人教A版11-2021-06-1616页