【精品试题】2021年高考数学一轮复习创优测评卷（新高考专用）测试卷07 不等式（原卷版） 5页

2021 年高考数学一轮复习不等式创优测评卷(新高考专用) 一、单选题（共 60 分，每题 5 分） 1．函数 （ ， ）与 的图象如图，则下列不等式一定成立的是（ ） A． B． C． D． 2．若增函数 与 轴交点是 ，则不等式 的解集是（ ） A． B． C． D． 3．偶函数 满足： ，且在区间 与 上分别递减与递增，则不等 式 的解集为（ ） A． B． C． D． 4．已知函数 与 满足： ，且 在区间 上 为减函数，令 ，则下列不等式正确的是（ ） A． B． C． D． 5．对于 ，给出下列四个不等式 （ ） ① ② ③ ④ 其中成立的是 A．①与③ B．①与④ C．②与③ D．②与④ 6．已知函数  f x 与  g x 满足：        2 2 , 1 1f x f x g x g x      ，且  f x 在区间 2, 上为 减函数，令      h x f x g x  ，则下列不等式正确的是（ ） A．    2 4h h  B．    2 4h h  C．    0 4h h D．    0 4h h 7．已知 *Nk  ， , , Rx y z  ，若 2 2 2( ) 5( )k xy yz zx x y z     ，则对此不等式描述正 确的是（ ） A．若 5k  ，则至少存在．．．．一个以 , ,x y z 为边长的等边三角形 B．若 6k  ，则对任意满足不等式的 , ,x y z 都存在．．．以 , ,x y z 为边长的三角形 C．若 7k  ，则对任意满足不等式的 , ,x y z 都存在．．．以 , ,x y z 为边长的三角形 D．若 8k = ，则对满足不等式的 , ,x y z 不存在．．．以 , ,x y z 为边长的直角三角形 8．设二次函数   2f x ax bx c   的导函数为  f x ，则对 x R  ，不等式    f x f x  恒成立，则 2 2 22 b a c 的最大值为 A． 6 2 B． 6 2 C． 6 2 D． 6 2 9．已知二次函数   2f x x px q   通过点 ,0 、 ,0 .若存在整数 n ，使 1n n     ，则     min , 1f n f n  与 1 4 的关系为（ ）. A．      1min , 1 4f n f n   B．      1min , 1 4f n f n   C．      1min , 1 4f n f n   D．不能确定，与 n 的具体取值有关 10．已知二次函数 ,方程 的两个根为 ,满足 ,那么 当 时, 与 的大小关系为( ) A． B． C． D． 11．已知向量 a ，b 均为非零向量，则下列说法不正确的个数是（ ） ①向量 a 与 b 反向，且 a b  ，则向量 a b  与 a 的方向相同； ②向量 a 与 b 反向，且 a b  ，则向量 a b  与 a 的方向相同； ③向量 a 与 b 同向，则向量 a b  与 a 的方向相同. 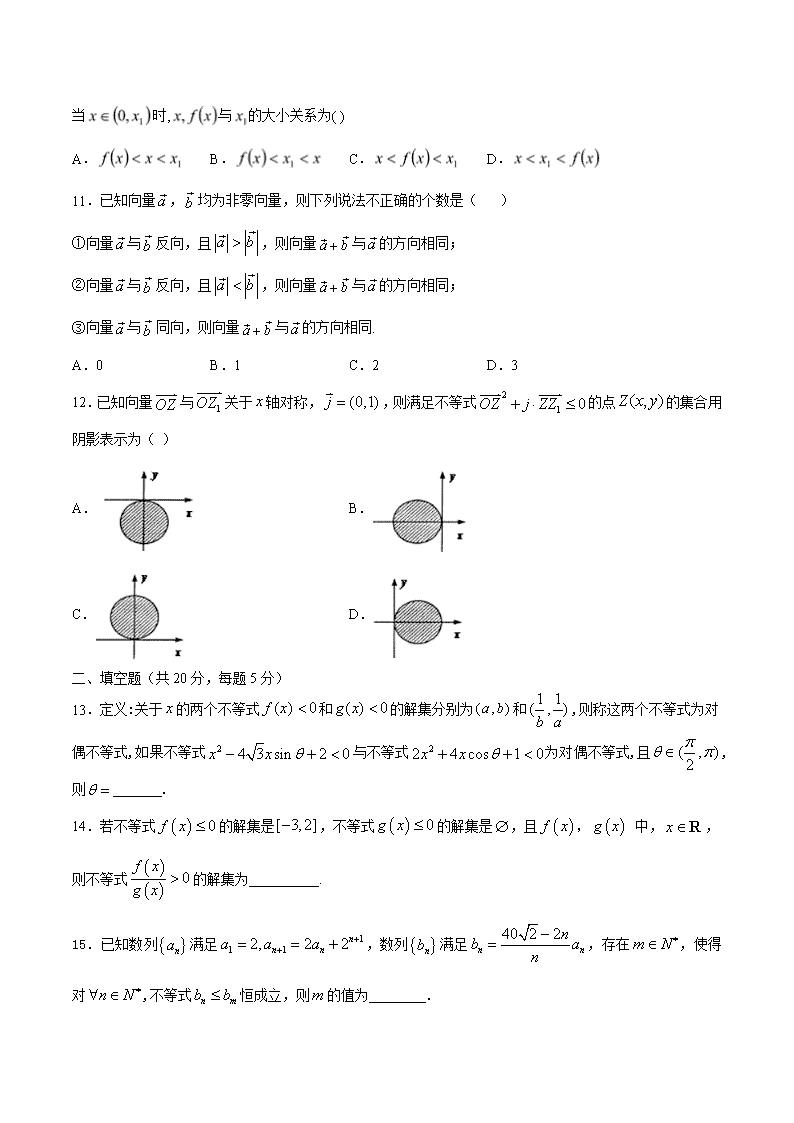A．0 B．1 C．2 D．3 12．已知向量OZ 与 1OZ 关于 x 轴对称， (0,1)j  ，则满足不等式 2 1 0OZ j ZZ    的点 ( , )Z x y 的集合用 阴影表示为（ ） A． B． C． D． 二、填空题（共 20 分，每题 5 分） 13．定义:关于 x 的两个不等式 ( ) 0f x  和 ( ) 0g x 的解集分别为 ( , )a b 和 1 1( , )b a ,则称这两个不等式为对 偶不等式,如果不等式 2 4 3 sin 2 0x x    与不等式 22 4 cos 1 0x x    为对偶不等式,且 ( , )2   , 则  _______. 14．若不等式   0f x  的解集是[ 3,2] ，不等式   0g x  的解集是，且  f x ，  g x 中， xR ， 则不等式     0f x g x  的解集为__________. 15．已知数列 na 满足 1 1 12, 2 2n n na a a     ，数列 nb 满足 40 2 2 n n nb an  ，存在 m N  ，使得 对 n N   ,不等式 n mb b 恒成立，则 m 的值为 ． 16．观察下列不等式： 1 2 1 22 a a a a  1 2 3 3 1 2 33 a a a a a a   1 2 3 4 4 1 2 3 44 a a a a a a a a    …… 照此规律，当 n N ( 2)n… 时不等式为__________. 三、解答题（共 70 分） 17． （10 分）已知函数    3 1f x x a x a R     . （1）当 1a   时，求不等式   1f x ≤ 的解集； （2）设关于 x 的不等式   3 1f x x  的解集为 M ，且 1 ,14 M     ，求 a 的取值范围. 18．（10 分）设函数    | 1| 2| |f x x x   － ，   2  1g x x mx  - ． （1）当   4m  - 时，求不等式     f x g x 的解集； （2）若不等式     f x g x 在 1[ 2, ]2   上恒成立，求实数  m 的取值范围． 19．（12 分）已知函数       2 21 1 2 2 ,2 xf x ax bx a b e x x x a R         ，且曲线  y f x 与 x 轴切于原点O ． （1）求实数 ,a b 的值； （2）若不等式   0f x  解集与不等式 2 0x mx n   的解集相同，求 m n 的值． 20．（12 分）已知函数   1 2 1f x m x x     ． （1）当 5m  时，求不等式   2f x  的解集； （2）若二次函数 2 2 3y x x   与函数  y f x 的图象恒有公共点，求实数 m 的取值范围． 21．（12 分）已知二次函数 2( )f x ax bx c   ，当 ( , 2) (0, )x     时， ( ) 0f x  ，当 ( 2,0)x  时， ( ) 0f x  ，且对任意 xR ，不等式 ( ) ( 1) 1f x a x   恒成立. （1）求函数 ( )f x 的解析式； （2）设函数 ( ) ( ) 3F x tf x x   ，其中 0t  ，求 ( )F x 在 3 ,22x      时的最大值 ( )H t . 22．（14 分）已知数列 na 满足  * 1 1 2 2 n n n a a n Na   ，且 1 1a  . （Ⅰ）证明：数列 1 na       为等差数列，并求数列 na 的通项公式； （Ⅱ）若记 nb 为满足不等式  * 1 1 1 2 2kn na n N   的正整数 k 的个数，设     11 1 n n n n n n bT b b      ， 求数列 nT 的最大项与最小项的值.