高中数学（人教版a版必修一）配套课时作业：第二章基本初等函数（ⅰ）2-3word版含解析 9页

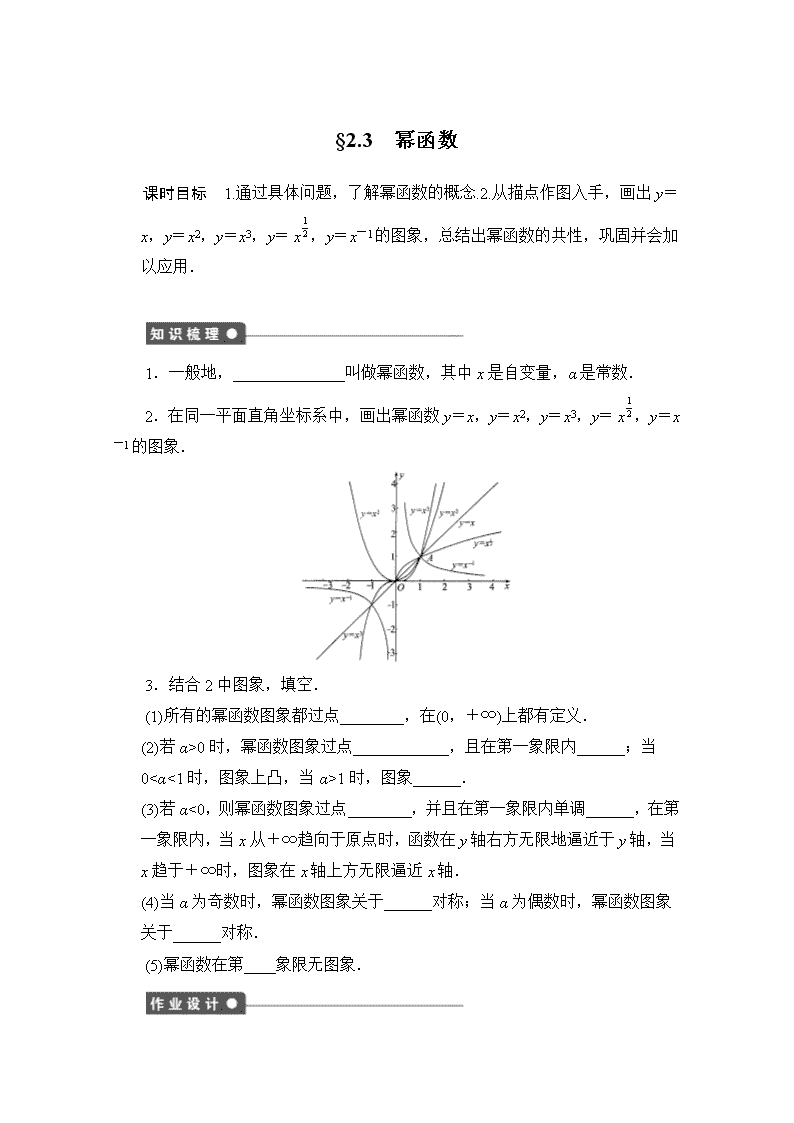
§2.3 幂函数 课时目标 1.通过具体问题，了解幂函数的概念.2.从描点作图入手，画出 y＝x， y＝x2，y＝x3，y＝ 1 2x ，y＝x－1 的图象，总结出幂函数的共性，巩固并会加以应 用． 1．一般地，______________叫做幂函数，其中 x 是自变量，α是常数． 2．在同一平面直角坐标系中，画出幂函数 y＝x，y＝x2，y＝x3，y＝ 1 2x ，y＝x －1 的图象． 3．结合 2 中图象，填空． (1)所有的幂函数图象都过点________，在(0，＋∞)上都有定义． (2)若α>0 时，幂函数图象过点____________，且在第一象限内______；当 0<α<1 时，图象上凸，当α>1 时，图象______． (3)若α<0，则幂函数图象过点________，并且在第一象限内单调______，在第 一象限内，当 x 从＋∞趋向于原点时，函数在 y 轴右方无限地逼近于 y 轴，当 x 趋于＋∞时，图象在 x 轴上方无限逼近 x 轴． (4)当α为奇数时，幂函数图象关于______对称；当α为偶数时，幂函数图象关 于______对称． (5)幂函数在第____象限无图象． 一、选择题 1．下列函数中不是幂函数的是( ) A．y＝ xB．y＝x3 C．y＝2xD．y＝x－1 2．幂函数 f(x)的图象过点(4，1 2)，那么 f(8)的值为( ) A. 2 4 B．64 C．2 2D. 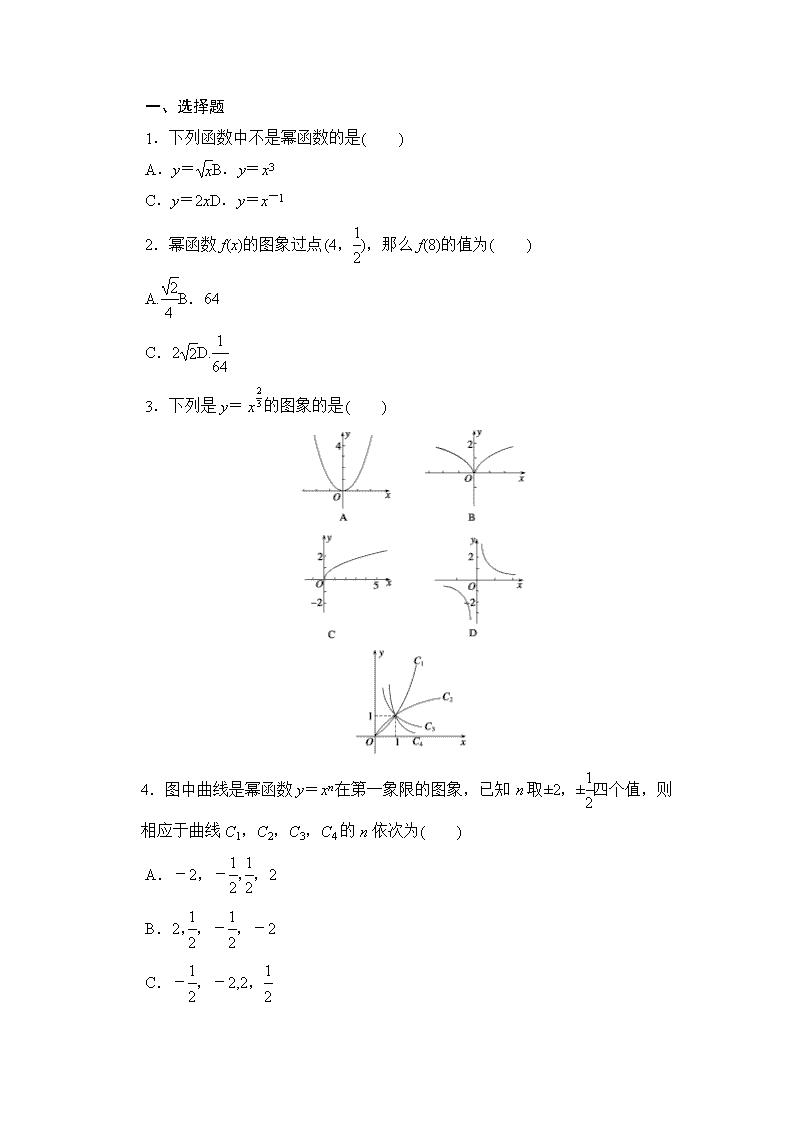1 64 3．下列是 y＝ 2 3x 的图象的是( ) 4．图中曲线是幂函数 y＝xn 在第一象限的图象，已知 n 取±2，±1 2 四个值，则 相应于曲线 C1，C2，C3，C4 的 n 依次为( ) A．－2，－1 2 ，1 2 ，2 B．2，1 2 ，－1 2 ，－2 C．－1 2 ，－2,2，1 2 D．2，1 2 ，－2，－1 2 5．设 a＝ 2 53 5      ，b＝ 3 52 5      ，c＝ 2 52 5      ，则 a，b，c 的大小关系是( ) A．a>c>bB．a>b>c C．c>a>bD．b>c>a 6．函数 f(x)＝xα，x∈(－1,0)∪(0,1)，若不等式 f(x)>|x|成立，则在α∈{－2，－ 1,0,1,2}的条件下，α可以取值的个数是( ) A．0B．2 C．3D．4 题 号 1 2 3 4 5 6 答 案 二、填空题 7．给出以下结论： ①当α＝0 时，函数 y＝xα的图象是一条直线； ②幂函数的图象都经过(0,0)，(1,1)两点； ③若幂函数 y＝xα的图象关于原点对称，则 y＝xα在定义域内 y 随 x 的增大而增 大； ④幂函数的图象不可能在第四象限，但可能在第二象限． 则正确结论的序号为________． 8．函数 y＝ 1 2x ＋x－1 的定义域是____________． 9．已知函数 y＝x－2m－3 的图象过原点，则实数 m 的取值范围是 ____________________． 三、解答题 10．比较 1. 1 21 、 1 21.4 、 1 31.1 的大小，并说明理由． 11．如图，幂函数 y＝x3m－7(m∈N)的图象关于 y 轴对称，且与 x 轴、y 轴均无 交点，求此函数的解析式． 能力提升 12．已知函数 f(x)＝(m2＋2m)· 2 1m mx   ，m 为何值时，函数 f(x)是：(1)正比例函 数； (2)反比例函数；(3)二次函数；(4)幂函数． 13．点( 2，2)在幂函数 f(x)的图象上，点(－2，1 4)在幂函数 g(x)的图象上，问 当 x 为何值时，有：(1)f(x)>g(x)；(2)f(x)＝g(x)；(3)f(x)0 时为增函数，n m<0 时为减函数． §2.3 幂函数 知识梳理 1．函数 y＝xα 3.(1)(1,1) (2)(0,0)，(1,1) 递增 下凸 (3)(1,1) 递减 (4)原点 y 轴 (5)四 作业设计 1．C [根据幂函数的定义：形如 y＝xα的函数称为幂函数，选项 C 中自变量 x 的系数是 2，不符合幂函数的定义，所以 C 不是幂函数．] 2．A [设幂函数为 y＝xα，依题意，1 2 ＝4α， 即 22α＝2－1，∴α＝－1 2. ∴幂函数为 y＝ 1 2x  ，∴f(8)＝ 1 28  ＝ 1 8 ＝ 1 2 2 ＝ 2 4 .] 3．B [y＝ 2 3x ＝3 x2，∴x∈R，y≥0，f(－x)＝3 －x2＝3 x2 ＝f(x)，即 y＝ 2 3x 是偶函数，又∵2 3<1，∴图象上凸．] 4．B [作直线 x＝t(t>1)与各个图象相交，则交点自上而下的排列顺序恰好是 按幂指数的降幂排列的．] 5．A [根据幂函数与指数函数的单调性直接可以判断出来，y＝ 2 5x 在 x>0 时 是增函数，所以 a>c；y＝(2 5)x 在 x>0 时是减函数，所以 c>b.] 6．B [因为 x∈(－1,0)∪(0,1)，所以 0<|x|<1. 要使 f(x)＝xα>|x|，xα在(－1,0)∪(0,1)上应大于 0， 所以α＝－1,1 显然是不成立的． 当α＝0 时，f(x)＝1>|x|； 当α＝2 时，f(x)＝x2＝|x|2<|x|； 当α＝－2 时，f(x)＝x－2＝|x|－2>1>|x|. 综上，α的可能取值为 0 或－2，共 2 个．] 7．④ 解析 当α＝0 时，函数 y＝xα的定义域为{x|x≠0，x∈R}，故①不正确；当α<0 时，函数 y＝xα的图象不过(0,0)点，故②不正确；幂函数 y＝x－1 的图象关于原 点对称，但其在定义域内不是增函数，故③不正确．④正确． 8．(0，＋∞) 解析 y＝ 1 2x 的定义域是[0，＋∞)，y＝x－1 的定义域是(－∞，0)∪(0，＋∞)， 再取交集． 9．m<－3 2 解析 由幂函数的性质知－2m－3>0， 故 m<－3 2. 10．解 考查函数 y＝1.1x，∵1.1>1， ∴它在(0，＋∞)上是增函数． 又∵1 2>1 3 ，∴ 1 21.1 > 1 31.1 . 再考查函数 y＝ 1 2x ，∵1 2>0， ∴它在(0，＋∞)上是增函数． 又∵1.4>1.1，∴ 1 21.4 > 1 21.1 ， ∴ 1 21.4 > 1 21.1 > 1 31.1 . 11．解 由题意，得 3m－7<0. ∴m<7 3. ∵m∈N，∴m＝0,1 或 2， ∵幂函数的图象关于 y 轴对称， ∴3m－7 为偶数． ∵m＝0 时，3m－7＝－7， m＝1 时，3m－7＝－4， m＝2 时，3m－7＝－1. 故当 m＝1 时，y＝x－4 符合题意．即 y＝x－4. 12．解 (1)若 f(x)为正比例函数， 则 m2＋m－1＝1， m2＋2m≠0 ⇒m＝1. (2)若 f(x)为反比例函数， 则 m2＋m－1＝－1， m2＋2m≠0 ⇒m＝－1. (3)若 f(x)为二次函数，则 m2＋m－1＝2， m2＋2m≠0 ⇒m＝－1± 13 2 . (4)若 f(x)为幂函数，则 m2＋2m＝1， ∴m＝－1± 2. 13．解 设 f(x)＝xα，则由题意，得 2＝( 2)α，∴α＝2，即 f(x)＝x2. 设 g(x)＝xβ，由题意，得1 4 ＝(－2)β， ∴β＝－2，即 g(x)＝x－2. 在同一平面直角坐标系中作出 f(x)与 g(x)的图象，如图所示． 由图象可知： (1)当 x>1 或 x<－1 时， f(x)>g(x)； (2)当 x＝±1 时，f(x)＝g(x)； (3)当－1