20届 高三上学期11月月考数学试题 22页

第 1 页 共 22 页 2020 届浙江省宁波市宁波十校高三上学期 11 月月考数学试 题 一、单选题 1．已知集合 A＝{x| 1 2 x x   0}，B＝{x|1＜x≤2}，则 A∩B＝（ ） A．{x|1＜x＜2} B．{x|1＜x≤2} C．{x|﹣1≤x≤2} D．{x|﹣1≤x＜2} 【答案】A 【解析】集合 A＝{x|﹣1≤x＜2}，集合的交集运算，即可求解. 【详解】 由题意，集合 A＝{x| 1 2 x x   0}＝{x|﹣1≤x＜2}，B＝{x|1＜x≤2}，所以 A∩B＝{x|1＜x＜ 2}． 故选：A． 【点睛】 本题主要考查了分式不等式的求解，以及集合的交集的运算，其中解答中正确求解集合 A，结合集合的交集概念及运算求解是解答的关键，着重考查了推理与计算能力，属于 基础题． 2．若复数  1 2 a i a Ri   为纯虚数，其中i 为虚数单位，则 a  （ ） A．2 B．3 C．-2 D．-3 【答案】C 【解析】因为 1 1( (1 2 ) [ 2 (1 2 ) ]1 2 5 5 a i a i i a a ii          ） 为纯虚数，所以 2 0a   且1 2 0a  ，解得 2a   ，故选 C． 点睛：复数是高考中的必考知识，主要考查复数的概念及复数的运算．要注意对实部、 虚部的理解，掌握纯虚数，共轭复数这些重要概念，复数的运算主要考查除法运算，通 过分母实数化，转化为复数的乘法，运算时特别要注意多项式相乘后的化简，防止简单 问题出错，造成不必要的失分． 3．已知三个实数 2，a，8 成等比数列，则双曲线 2 2 2 19 y x a   的渐近线方程为（ ） A．3x±4y＝0 B．4x±3y＝0 C． 3 x±2y＝0 D．9x±16y＝0 【答案】A 第 2 页 共 22 页 【解析】由三个实数 2， a ，8 成等比数列，求得 2a ＝16，得到双曲线 2 2 19 16 y x  的 渐近线方程，即可求得双曲线的渐近线的方程，得到答案． 【详解】 由题意，三个实数 2， a ，8 成等比数列，可得 2a ＝16， 即双曲线 2 2 19 16 y x  的渐近线方程为 3x±4y＝0， 故选：A． 【点睛】 本题主要考查了双曲线的标准方程及简单的几何性质，其中解答中根据等比中项公式， 求得 a 的值，得出双曲线的标准方程式解答的关键，着重考查了推理与运算能力，属于 基础题． 4．若实数 x，y 满足 x+y＞0，则“x＞0”是“x2＞y2”的（ ） A．充分不必要条件 B．必要不充分条件 C．充分必要条件 D．既不充分也不必要条件 【答案】B 【解析】根据充分条件、必要条件的判定方法，结合不等式的性质，即可求解，得到答 案． 【详解】 由题意，实数 x，y 满足 x+y＞0，若 x＞0，则未必有 x2＞y2， 例如 x＝1，y＝2 时，有 x2＜y2； 反之，若 x2＞y2，则 x2﹣y2＞0，即（x+y）（x﹣y）＞0； 由于 x+y＞0，故 x﹣y＞0，∴x＞y 且 x＞﹣y，∴x＞0 成立； 所以当 x+y＞0 时，“x＞0”推不出“x2＞y2”，“x2＞y2”⇒“x＞0”； ∴“x＞0”是“x2＞y2”的必要不充分条件． 答案：B． 【点睛】 本题主要考查了不等式的性质，以及充分条件、必要条件的判定，其中解答中熟记充分 条件、必要条件的判定方法，结合不等式的性质求解是解答的关键，着重考查了推理与 论证能力，属于基础题． 5．已知函数 f（x）＝x2﹣3x﹣3，x∈[0，4]，当 x＝a 时，f（x）取得最大值 b，则函 第 3 页 共 22 页 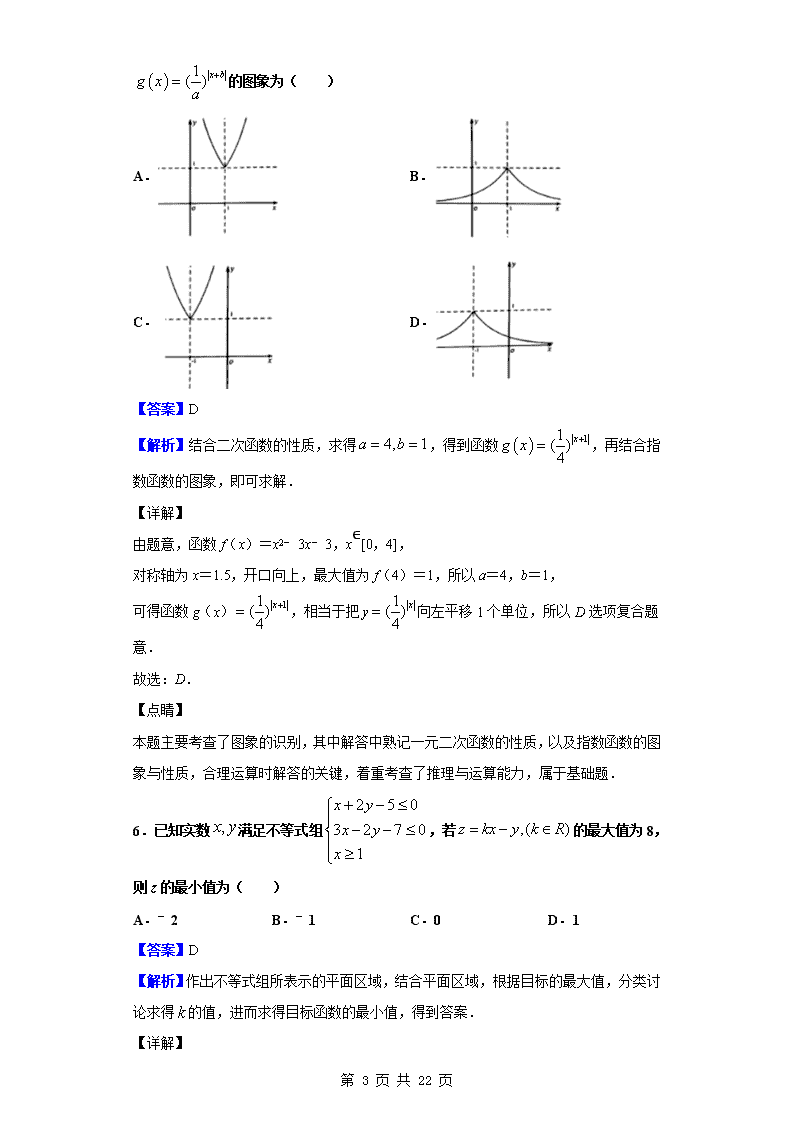数   1( ) x bg x a  的图象为（ ） A． B． C． D． 【答案】D 【解析】结合二次函数的性质，求得 4, 1a b  ，得到函数   11( )4 xg x  ，再结合指 数函数的图象，即可求解． 【详解】 由题意，函数 f（x）＝x2﹣3x﹣3，x∈[0，4]， 对称轴为 x＝1.5，开口向上，最大值为 f（4）＝1，所以 a＝4，b＝1， 可得函数 g（x） 11( )4 x ，相当于把 y 1( )4 x 向左平移 1 个单位，所以 D 选项复合题 意． 故选：D． 【点睛】 本题主要考查了图象的识别，其中解答中熟记一元二次函数的性质，以及指数函数的图 象与性质，合理运算时解答的关键，着重考查了推理与运算能力，属于基础题． 6．已知实数 ,x y 满足不等式组 2 5 0 3 2 7 0 1 x y x y x          ，若 ,( )z kx y k R   的最大值为 8， 则 z 的最小值为（ ） A．﹣2 B．﹣1 C．0 D．1 【答案】D 【解析】作出不等式组所表示的平面区域，结合平面区域，根据目标的最大值，分类讨 论求得 k 的值，进而求得目标函数的最小值，得到答案． 【详解】 第 4 页 共 22 页 由题意，作出不等式组 2 5 0 3 2 7 0 1 x y x y x          所表示的可行域，如图所示， 由 1 3 2 7 0 x x y      ，解得 (1, 2)A  ；由 2 5 0 3 2 7 0 x y x y        ，解答 (3,1)B ； 由 2 5 0 1 x y x      ，解得 (1,2)C （1）若目标函数取得最大值8 的最优解为 (1, 2)A  时，代入目标函数，可得 6k  ， 此时目标函数 6z x y  ，此时代入点 (3,1)B ，可得 6 3 1 17 8z      ，不符合题 意； （2）若目标函数取得最大值8 的最优解为 (1,2)C 时，代入目标函数，可得 10k  ， 此时目标函数 10z x y  ，此时代入点 (3,1)B ，可得 10 3 1 29 8z      ，不符合 题意； （3）若目标函数取得最大值8 的最优解为 (3,1)B 时，代入目标函数，可得 3k  ， 此时目标函数 3z x y  ，此时点C 能使得目标函数取得最小值，代入点 (1,2)C ， 最小值为 3 1 2 1z     ； 答案：D． 【点睛】 本题主要考查简单线性规划求解目标函数的最值问题．其中解答中正确画出不等式组表 示的可行域，利用“一画、二移、三求”，确定目标函数的最优解是解答的关键，着重考 查了数形结合思想，及推理与计算能力，属于基础题． 7．函数 f（x）＝sin（ωx+φ）（ω＞0， 2 2   ＜ ＜ ）满足 f（ 4  ）＝f（ 2  ）＝﹣f（ 3 4  ）， 第 5 页 共 22 页 且当 x∈[ 4  ， 2  ]时恒有 f（x）≥0，则（ ） A．ω＝2 B．ω＝4 C．ω＝2 或 4 D．ω不确定 【答案】A 【解析】根据三角函数的图象与性质，求得函数的对称轴和对称点，判断周期T 的取值 范围，即可求解，得到答案． 【详解】 由题意，函数   ( )sin   f x x ，因为 f（ 4  ）＝f（ 2  ）＝﹣f（ 3 4  ）， 可得 f（x）有一条对称轴为 34 2 2 8x      ，对称点的横坐标为 3 52 4 2 8     ， 又由 x∈[ 4  ， 2  ]时恒有 f（x）≥0，所以 f（ 3 8  ）＝1，又 f（ 5 8  ）＝0，5 3 8 8 4     ． 所以 4 4 T  ， 3 4 4 T  ， 可得当 T＝π，ω＝2；当 T 3  时，ω＝6， 当 x 3 4  时，sin（6• 3 4   φ）＝cosφ＞0，不成立， 故选：A． 【点睛】 本题主要考查了三角函数的图象与性质的应用，其中解答中熟记三角函数的图象与性 质，准确计算是解答的关键，着重考查了分析问题和解答问题的能力，属于中档试题． 8．今有男生 3 人，女生 3 人，老师 1 人排成一排，要求老师站在正中间，女生有且仅 有两人相邻，则共有多少种不同的排法？（ ） A．216 B．260 C．432 D．456 【答案】C 【解析】将老师两边分别看作三个位置，先分组再排列，在排入学生，按分步计数原理， 即可求解． 【详解】 由题意，将老师两边分别看作三个位置，将学生分为两女一男和两男一女两组，且两女 相邻，分组方法有 2 1 3 3C C  9 种， 两女一男的排列方法为 2 2 2 2A A  4 种， 第 6 页 共 22 页 两男一女的排列方法有 3 3A  6 种， 由分步计数原理，可得总的排列方法有 2 29 4 6 A    432 种， 故选：C． 【点睛】 本题主要考查了计数原理、排列组合的应用，其中解答中认真审题，合理利用排列、组 合的知识求解是解答的关键，着重考查了分析问题和解答问题的能力，属于基础题． 9．如图，点 E 为正方形 ABCD 边 CD 上异于点 C、D 的动点，将△ADE 沿 AE 翻折成 △SAE，在翻折过程中，下列三个说法中正确的个数是（ ） ①存在点 E 和某一翻折位置使得 AE∥平面 SBC； ②存在点 E 和某一翻折位置使得 SA⊥平面 SBC； ③二面角 S﹣AB﹣E 的平面角总是小于 2∠SAE． A．0 B．1 C．2 D．3 【答案】B 【解析】对于①，四边形 ABCE 为梯形，所以 AE 与 BC 必然相交；对于②，假设 SA  平面 SBC，可推得矛盾；对于③，当将△ADE 沿 AE 翻折使得平面 SAE⊥平面 ABCE 时， 二面角 S﹣AB﹣E 最大，在平面 SAE 内，作出一个角等于二面角 S﹣AB﹣E 的平面角； 由角 SAE 所在三角形的一个外角，它是不相邻的两个内角之和，结合图形，即可判 定③． 【详解】 对于①，四边形 ABCE 为梯形，所以 AE 与 BC 必然相交，故①错误； 对于②，假设 SA  平面 SBC，SC  平面 SBC，所以 SA⊥SC，又 SA⊥SE，SE∩SC＝S， 所以 SA⊥平面 SCE，所以平面 SCE∥平面 SBC，这与平面 SBC∩平面 SCE＝SC 矛盾， 故假设不成立，即②错误； 对于③，当将△ADE 沿 AE 翻折使得平面 SAE⊥平面 ABCE 时，二面角 S﹣AB﹣E 最大， 如图，在平面 SAE 内，作 SO⊥AE，垂足为 O，∴SO⊥平面 ABCE；AB  平面 ABCE， 所以 SO⊥AB； 作 OF⊥AB，垂足为 F，连接 SF，SO∩OF＝O，则 AB⊥平面 SFO，所以 AB⊥SF，则 第 7 页 共 22 页 ∠SFG 即为二面角 S﹣AB﹣E 的平面角； 在直线 AE 上取一点 1F ，使得 O 1F ＝OF，连接 S 1F ，则∠S 1F O＝∠SFO； 由图形知，在△SA 1F 中，S 1F ＞A 1F ，所以∠AS 1F ＜∠SAE；而∠S 1F O＝∠SAE+∠AS 1F ， 故∠S 1F O＜2∠SAE； 即∠SFO＜2∠SAE．故③正确． 故选：B． 【点睛】 本题主要考查了空间中的平行于垂直关系的应用，二面角的平面角的作法，以及立体几 何的折叠问题，其中解答中熟记线面关系的判定与性质，以及熟练掌握二面角的平面角 的作法是解答的关键，着重考查了空间想象能力，以及转化思想的应用，属于中档试题． 10．已知函数 f（x） 2 0 0 xe x lnx x      ， ， ＞ ，g（x）＝f（ 2 1 3 kx  ）+1（k∈R，k≠0），则下 列关于函数 y＝f[g（x）]+1 的零点个数判断正确的是（ ） A．当 k＞0 时，有 2 个零点；当 k＜0 时，有 4 个零点 B．当 k＞0 时，有 4 个零点；当 k＜0 时，有 2 个零点 C．无论 k 为何值，均有 2 个零点 D．无论 k 为何值，均有 4 个零点 【答案】B 【解析】根据方程的跟和函数的零点的关系，将函数 [ ( )] 1y f g x  的零点个数转化为 2 1 3 kxy  和 1y e  以及 1 1ey e   的交点，即可求解． 【详解】 依题意，当 x＝0 或 x 1 e  时，f（x）＝﹣1， 函数 y＝f[g（x）]+1 的零点个数，即为方程 f[g（x）]＝﹣1 的解的个数， 即为方程 g（x）＝0 或 g（x） 1 e  的解的个数， 第 8 页 共 22 页 即为方程 2 2 1 03 1 03 kx kx      或者 2 2 1 03 1 1 3 kx kx e      或 2 2 1 03 1 1 13 kx kx ln e            （舍去） 或者 2 12 1 1 03 1 3 e kx kx e          解的个数， 即为 2 1 3 kx   0 或者 2 1 1 3 kx e   或者 12 11 3 ekx e      解的个数， 由 10 3  ， 1 1 3e  ，因为 1 1 11 1 11 1 1( ) 03 e e ee e e ee        ，所以 1 1 1 3 ee   ， ①当 k＞0 时，y 2 1 3 kx  为顶点为（0， 1 3 ），开口向上的抛物线，y 2 1 3 kx  与 y 1 e  和 1 1ey e   分别有两个交点，与 y＝0 无交点， 故当 k＞0 时，函数 y＝f[g（x）]+1 有 4 个零点； ②当 k＜0 时，y 2 1 3 kx  为顶点为（0， 1 3 ），开口向下的抛物线，y 2 1 3 kx  与 y＝0 有两个交点，与 y 1 e  和 1 1ey e   无交点， 故当 k＜0 时，函数 y＝f[g（x）]+1 有 2 个零点； 综上，当 k＞0 时，有 4 个零点；当 k＜0 时，有 2 个零点， 故选：B． 【点睛】 本题主要考查了函数的零点与方程的跟的关系，以及函数的零点个数问题，其中解答中 将函数 [ ( )] 1y f g x  的零点个数转化为 2 1 3 kxy  和 1y e  以及 1 1ey e   的交点是 解答的关键，着重考查了分析问题和解答问题的能力，属于难题． 二、填空题 11．已知θ∈（0，π），且 sin（ 4   θ） 2 10  ，则 cos（θ 4  ）＝_____，sin2θ＝_____． 【答案】 2 10 24 25 第 9 页 共 22 页 【解析】由已知直接利用诱导公式求得 cos( )4   ，再由 sin 2 cos( 2 ) cos[2( )]2 4        ，利用余弦的倍角公式，即可求解． 【详解】 由题意，因为 sin（ 4   θ） 2 10  ， 可得 cos（θ 4  ）＝cos[ 2   （ 4   ）]＝sin（ 4   θ） 2 10  ； 又由 sin2θ＝cos（ 22   ）＝cos2（ 4   ） 2 22 241 2 1 2 ( )4 10 25sin            ． 故答案为： 2 10 ， 24 25 ． 【点睛】 本题主要考查了三角函数的诱导公式、以及余弦的倍角公式的化简求值问题，其中解答 中熟记三角函数的诱导公式和三角函数恒等变换的公式，准确运算是解答的关键，着重 考查了推理与运算能力，属于基础题． 12．在二项式 52( )x x  的展开式中，各项系数的和为_____，含 x 的一次项的系数为 _____．（用数字作答） 【答案】 1 10 【解析】令 1x  ，代入即可求得展开式各项系数的和，再写出二项展开式的通项，令 x 的指数为 1，求得 r 的值，即可求得 x 的一次项系数，得到答案． 【详解】 在二项式 52( )x x  中，取 1x  ，可得各项系数的和为﹣1； 二项式 52( )x x  的展开式的通项 5 3 5 2 1 5 5 2( ) ( ) ( 2) r r r r r r rT C x C xx        ． 由 5 3 12 r  ，得 r＝1． ∴含 x 的一次项的系数为 1 52 10C   ． 故答案为：﹣1；﹣10． 【点睛】 本题主要考查了二项式定量的应用，其中解答中合理利用赋值法，以及熟记二项展开式 的通项，准确运算是解答的关键，着重考查了推理与运算能力，属于基础题． 第 10 页 共 22 页 13．祖暅是我国南北朝时代的伟大科学家，他在实践的基础上提出了体积计算的原理： “幂势既同，则积不容异”，称为祖暅原理．意思是底面处于同一平面上的两个同高的几 何体，若在等高处的截面面积始终相等，则它们的体积相等．利用这个原理求半球 O 的体积时，需要构造一个几何体，该几何体的三视图如图所示，则该几何体的体积为 _____，表面积为_____． 【答案】 2 3  （3 2+ ）π 【解析】根据给定的几何体的三视图，得到该几何体为一个圆柱挖去一个圆锥，得出圆 柱的底面半径和高，利用体积和侧面积、以及圆的公式，即可求解． 【详解】 根据给定的几何体的三视图，可得该几何体表示一个圆柱挖去一个圆锥， 且底面半径 1，高为 1 的组合体， 所以几何体的体积为： 2 2 21 311 1 13       ． 几何体的表面积为： 2 11 2 1 2 1 12           （3 2+ ）π， 故答案为： 2 3  ，（3 2+ ）π 【点睛】 本题考查了几何体的三视图及体积的计算，在由三视图还原为空间几何体的实际形状 时，要根据三视图的规则，空间几何体的可见轮廓线在三视图中为实线，不可见轮廓线 在三视图中为虚线，求解以三视图为载体的空间几何体的表面积与体积的关键是由三视 图确定直观图的形状以及直观图中线面的位置关系和数量关系，利用相应公式求解． 14．一个袋中装有 10 个大小相同的黑球、白球和红球．已知从袋中任意摸出 2 个球， 至少得到一个白球的概率是 7 9 ，则袋中的白球个数为_____，若从袋中任意摸出 3 个球， 记得到白球的个数为ξ，则随机变量ξ的数学期望 Eξ＝_____． 第 11 页 共 22 页 【答案】5 3 2 【解析】根据至少得到一个白球的概率为 7 9 ，可得不含白球的概率为 2 9 ，结合超几何 分布的相关知识可得白球的个数，以及随机变量的期望，得到答案． 【详解】 依题意，设白球个数为 x ，至少得到一个白球的概率是 7 9 ，则不含白球的概率为 2 9 ， 可得 2 10 2 10 2 9 xC C   ，即 (10 )(9 ) 20x x   ，解得 5x  ， 依题意，随机变量 ~ (10,5,3)H ，所以 3 5 3 10 2E   ． 故答案为：5， 3 2 ． 【点睛】 本题主要考查了超几何分布中事件的概率，以及超几何分布的期望的求解，其中解答中 熟记超几何分布的相关知识，准确计算是解答的关键，着重考查了分析问题和解答问题 的能力，属于中档试题． 15．已知常数 p＞0，数列{an}满足 an+1＝|p﹣an|+2an+p（n∈N），首项为 a1，前 n 项和 为 Sn．若 Sn≥S3 对任意 n∈N 成立，则 1a p 的取值范围为_____． 【答案】[﹣6，﹣4] 【解析】首先判断数列 na 为递增数列，结合 3nS S 恒成立，则必有 1 2 3 40a a a a    成立，用 1a 及 p 表示出 3 4,a a ，由不等式即可求解 1a p 的取值范围． 【详解】 由题意， 1 2 0           n n n n n na a p a a p p a a p p ， 及 1 0n na a   ，所以数列 na 为递增数列， 要使得 3nS S 对任意 n N  恒成立，则必有 3 40, 0a a  ， 所以 2 1 1 1 12 2 0a p a a p p a a p         ， 3 2 2 1 1 1 1 12 2 5 ( ) 2 5 4 0a p a a p a p a p a p a p a p                ， 4 3 3 1 1 1 1 12 3 2 9 ( 3 ) 2 9 6 0a p a a p a p a p a p a p a p                ， 第 12 页 共 22 页 所以 16 4a p     ，即 1a p 的取值范围[ 6, 4]  ． 故答案为：[ 6, 4]  ． 【点睛】 本题主要考查了数列的递推关系式的应用，其中解答的难点在于利用已知条件去掉绝对 值，并判断出 3 4,a a 满足的条件，着重考查了逻辑推理能力，属于中档试题． 16．已知椭圆 2 2 110 6 x y  ，倾斜角为 60°的直线与椭圆分别交于 A、B 两点且 8 30 9AB  ，点 C 是椭圆上不同于 A、B 一点，则△ABC 面积的最大值为_____． 【答案】16 30 9 【解析】设直线 AB 的方程为 3y x m  ，联立方程组，利用根与系数的关系及弦长 公式，得到    2 1 2 1 2 8 301 3 [ ) 4 9x x x x     ，解得 m 的值，设与直线 AB 平行且与椭圆相切 的直线方程为 3y x t  ，联立方程组，利用 0  ，求得 t 的值，再由点到直线的距 离公式和三角形的面积公式，即可求解． 【详解】 由题意，设直线 AB 的方程为 3y x m  ，点 A（x1，y1），B（x2，y2）， 联立方程组 2 2 3 110 6 y x m x y      ，整理得 18x2+10 3 mx+5m2﹣30＝0， 所以 x1+x2 5 3 9 m ，x1x2 25 30 18 m  ． 因为 8 30 9AB  ，即    2 1 2 1 2 8 301 3 [ ) 4 9x x x x     ， 代入整理得 2 4m  ，解得 2m   ， 不妨取：m＝2，可得直线 AB 的方程为 3 2y x  ， 设与直线 AB 平行且与椭圆相切的直线方程为 y 3 x+t， 第 13 页 共 22 页 联立方程组 2 2 3 110 6 y x t x y      ，整理得 18x2+10 3 tx+5t2﹣30＝0， 由△＝300t2﹣72×（5t2﹣30）＝0，解得：t＝±6． 取 t＝﹣6 时，与直线 AB 平行且与椭圆相切的直线与直线 AB 的距离 2 8 4 1 ( 3) d    ， 所以△ABC 面积的最大值 1 2S d AB 1 8 30 16 3042 9 9     ， 故答案为： 16 30 9 ． 【点睛】 本题主要考查了直线与圆锥曲线的位置关系的综合应用,解答此类题目，通常联立直线 方程与椭圆（圆锥曲线）方程，应用一元二次方程根与系数的关系进行求解，此类问题 易错点是复杂式子的变形能力不足，导致错解，能较好的考查考生的逻辑思维能力、运 算求解能力、分析问题解决问题的能力等． 17．已知平面向量 a ，b ，c 满足：a ，b 的夹角为 4  ，| a b  |＝5，c a  ，c b  的 夹角为 3 4  ，| c a  |＝3 2 ，则 a •c 的最大值为_____． 【答案】36 【解析】设 PA a  ， PB b  ， PC c  ，由题意知 , , ,P A B C 四点共圆，建立坐标系， 求出点C 的坐标和圆的半径，设 5 2 5 2( cos , sin )2 2P   ，用 表示 a c  ，根据 范 围和三角和差公式，即可求解． 【详解】 设 PA a  ， PB b  ， PC c  ， 则 AB＝| a b  |＝5，AC＝| c a  |＝3 2 ，∠ACB 3 4  ，∠APB 4  ， 可得 P，A，B，C 四点共圆． 设△ABC 的外接圆的圆心为 O，则∠AOB＝2∠APB 2  ， 由正弦定理可知：2OA AB sin ACB  5 2 ，故 OA 5 2 2  ． 第 14 页 共 22 页 以 O 为圆心，以 OA，OB 为坐标轴建立平面坐标系如图所示： 则 A（ 5 2 2 ，0），B（0， 5 2 2  ）． 在△OAC 中，由余弦定理可得 cos∠AOC 25 25 18 72 2 255 2 5 22 2 2       ， 故 sin∠AOC 24 25  ，∴C（ 7 2 10 ， 12 2 5  ）． 设 P（ 5 2 2 cosα， 5 2 2 sinα）， 30 2   ， 则 PA  （ 5 2 5 2 2 2  cosα， 5 2 2  sinα）， PC  （ 7 2 5 2 10 2  cosα， 12 2 5 2 5 2   sinα）， ∴ a c   （ 5 2 5 2 2 2  cosα）（ 7 2 5 2 10 2  cosα） 5 2 2  sinα（ 12 2 5 2 5 2  sinα） ＝16+12sinα﹣16cosα＝16+20•（ 3 5 sinα 4 5  cosα） ＝16+20sin（α﹣φ），其中 sinφ 4 5  ，cosφ 3 5  ． ∴当α＝φ 2  时， a c  取得最大值 36． 答案：36． 【点睛】 本题主要考查了向量的数量积的运算，正弦定理、余弦定理的应用，以及三角恒等变换 与三角函数的图象与性质的综合应用，着重考查了逻辑推理能力和分析问题和解答问题 第 15 页 共 22 页 的能力，属于难题． 三、解答题 18．已知△ABC 的内角 A、B、C 的对边分别为 a、b、c，且 3b csinA acosC  ． （1）求 A； （2）若 3a  ，求△ABC 的面积 S 的最大值． 【答案】（1）A 6  （2） 6 3 3 4  【解析】（1）利用整下定理，三角函数的恒等变换，集合 sin 0C  ，求得 3tan 3A  ， 即可求解； （2）由余弦定理，基本不等式求得bc 的最大值，进而根据三角形的面积公式，即可求 解三角形的最大面积． 【详解】 （1）由题意，在 ABC 中， 3b csinA acosC  ， 由正弦定理得sin 3sin sin sin cosB C A A C  ， 又由 A B C    ， 可得sin sin[ ( )] sin( ) sin cos cos sinB A C A C A C A C       所以sin cos cos sin 3sin sin sin cosA C A C C A A C   ， 即 cosAsinC 3 sinCsinA， 又因为 sinC≠0，所以 cosA 3 sinA，可得 tanA 3 3  ， 又由 A∈（0，π），∴A 6  ． （2）由余弦定理可得 cosA 2 2 2 3 2 2 b c a bc    ， 可得 b2+c2﹣3 3 bc， 因为 b2+c2≥2bc，所以 3 3 bc≥2bc，可得 bc 3 2 3    3（2 3 ）， 所以三角形的面积 S 1 2  bcsin 6 3 3 3 4   ，当且仅当 b＝c  3 2 3  等号成立， 第 16 页 共 22 页 所以△ABC 的面积 S 的最大值 6 3 3 4  ． 【点睛】 本题主要考查了正弦定理、余弦定理和三角形的面积公式的应用，其中在解有关三角形 的题目时，要有意识地考虑用哪个定理更合适，要抓住能够利用某个定理的信息．一般 地，如果式子中含有角的余弦或边的二次式时，要考虑用余弦定理；如果式子中含有角 的正弦或边的一次式时，则考虑用正弦定理，着重考查了运算与求解能力，属于基础题． 19．如图，四边形 ABCD 为菱形，四边形 ACFE 为平行四边形，设 BD 与 AC 相交于 点 G，AB＝BD＝AE＝2，∠EAD＝∠EAB． （1）证明：平面 ACFE⊥平面 ABCD； （2）若直线 AE 与 BC 的夹角为 60°，求直线 EF 与平面 BED 所成角的余弦值． 【答案】（1）证明见解析（2） 1 3 【解析】（1）先由已知条件求得 EAD EAB   ，得到 EG BD ，再结合菱形的对角 线垂直，可得 BD  平面 ACEF ，即可证得平面 ACFE⊥平面 ABCD； （2）建立空间直角坐标系，求得各点的坐标，设 E 的坐标，根据条件求出 E ，再求得 直线的方向向量和平面的法向量，利用向量的夹角公式，即可求解． 【详解】 （1）证明：连接 EG，因为 AB＝BD＝AE＝2，∠EAD＝∠EAB， 可得△EAD≌EAB，∴ED＝EB． ∵G 为 BD 的中点，所以 EG⊥BD，因为四边形 ABCD 为菱形，∴AC⊥BD， ∴BD⊥平面 ACEF，因为 BD⊂平面 ABCD； ∴平面 ACFE⊥平面 ABCD； 第 17 页 共 22 页 （2）因为 EF∥AG，直线 EF 与平面 BED 所成角即为 AG 与平面 BED 所成角； 以 G 为原点建立如图所示空间直角坐标系，如图所示， 设 E（a，0，b）则 AE  （a 3 ，0，b）， 因为 BC  （ 3 ，﹣1，0）， 所以由条件可得：| AE  |2＝（a 3 ）2+b2＝4 且 AE  • 3BC   a+3＝2×2×cos60°＝2； 解得 3 3 2 6 3 a b     ，所以 BE  （ 3 3 ，﹣1， 2 6 3 ），因为 DB  （0，2，0）； 所以可取平面 BED 的法向量 n  （2 2 ，0，﹣1），因为 EF AC   （﹣2 3 ，0，0）， 设直线 EF 与平面 BED 所成角为θ，则 sinθ 2 2 3 n EF n EF       ， ∵0＜θ 2  ；∴sosθ 2 11 3sin    ； 既直线 EF 与平面 BED 所成角的余弦值为 1 3 ． 【点睛】 本题考查了线面位置关系的判定与证明，以及空间角的求解问题，意在考查学生的空间 想象能力和逻辑推理能力，解答中熟记线面位置关系的判定定理和性质定理，通过严密 推理是线面位置关系判定的关键，同时对于立体几何中角的计算问题，往往可以利用空 间向量法，通过求解平面的法向量，利用向量的夹角公式求解. 第 18 页 共 22 页 20．已知等差数列{an}的前 n 项和为 Sn，且 a2+2a4＝a9，S6＝36． （1）求 an，Sn； （2）若数列{bn}满足 b1＝1， 1n n nb b S  ，求证： 1 2 1 1 1 2 1 n nb b b      （n∈N）． 【答案】（1）an＝2n﹣1，Sn＝n2（2）证明见解析 【解析】（1）设等差数列 na 的公差为 d ，运用等差数列的通项公式和求和公式，解 方程可得首项和公差，再结合等差数列的通项公式和求和公式，即可求解； （2）讨论 1, 2n n  ，将 n 换为 1n  ，相减得到 1 1 1 n n n b bb    ，再由数列的裂项相 消求和及不等式的性质，即可求解． 【详解】 （1）设等差数列{an}的公差设为 d，前 n 项和为 Sn，且 a2+2a4＝a9，S6＝36， 可得 a1+d+2（a1+3d）＝a1+8d，即 2a1＝d， 又 6a1+15d＝36，即 2a1+5d＝12， 解得 a1＝1，d＝2，则 an＝1+2（n﹣1）＝2n﹣1，Sn＝n+n（n﹣1）＝n2； （2）证明：数列{bn}满足 b1＝1， 1n n nb b S   n， 当 n＝1 时，b1b2＝1，可得 b2＝1， n≥2 时，bnbn﹣1＝n﹣1， 相减可得 bn（bn+1﹣bn﹣1）＝1，即 1 nb  bn+1﹣bn﹣1， 当 n≥2 时， 1 2 1 1 1 1 1 nb b b b      b3﹣b1+b4﹣b2+b5﹣b3+…+bn+1﹣bn﹣1 1 1 b   b1﹣b2+bn+bn+1≥﹣1+2 1n nb b   2 n  1； 当 n＝1 时， 1 1 b  1＝2 1 1，不等式成立， 综上可得， 1 2 1 1 1 2 1 n nb b b      （n∈N）． 【点睛】 本题主要考查了等差数列的通项公式和前 n 项和公式的应用，以及数列与不等式的证 明，其中解答中注意数列的裂项相消法求和，以及不等式的性质的应用是解答的关键， 第 19 页 共 22 页 着重考查了方程思想以及运算能力，属于中档试题． 21．如图，P 是抛物线 E：y2＝4x 上的动点，F 是抛物线 E 的焦点． （1）求|PF|的最小值； （2）点 B，C 在 y 轴上，直线 PB，PC 与圆（x﹣1）2+y2＝1 相切．当|PF|∈[4，6]时， 求|BC|的最小值． 【答案】（1）|PF|的最小值为 1（2） 2 35 3 【解析】（1）求得抛物线的焦点和准线方程，运用抛物线的定义和性质，即可求得|PF| 的最小值； （2）设 2 0 0 0 0(0, ), (0, ), ( , ), 4B m C n P x y y x ，分别求得 ,PB PC 的方程，运用直线和 圆相切，得到 ,m n 为方程 2 0 0 0( 2) 2 0x x y x x    的两根，再由韦达定理可得 m n ， 进而可求得其最小值． 【详解】 （1）P 是抛物线 E：y2＝4x 上的动点，F 是抛物线 E 的焦点（1，0），准线方程为 x＝ ﹣1， 由抛物线的定义可得|PF|＝d＝xP+1， 由 0Px  ，可得 d 的最小值为 1，|PF|的最小值为 1； （2）设 2 0 0 0 0(0, ), (0, ), ( , ), 4B m C n P x y y x ， 则 PB 的方程为 y 0 0 y m x  x+m，PC 的方程为 y 0 0 y n x  x+n， 由直线 PA 与圆（x﹣1）2+y2＝1 相切，可得 0 0 2 2 0 0( ) y m mx x y m      1， 整理得（x0﹣2）m2+2y0m﹣x0＝0， 同理可得（x0﹣2）n2+2y0n﹣x0＝0， 第 20 页 共 22 页 即有 m，n 为方程（x0﹣2）x2+2y0x﹣x0＝0 的两根，可得 m+n 0 0 2 2 y x   ，mn 0 02 x x   ， 则|m﹣n| 22 0 02 0 0 2 0 0 0 4 84 4( ) 4 (2 ) 2 2 x xy xm n mn x x x         ， 由|PF|∈[4，6]，可得 x0+1∈[4，6]，即 x0∈[3，5]， 令 t＝|2﹣x0|＝x0﹣2，t∈[1，3]， 即有|m﹣n|  24(2 ) 8 2t t t      2 2 8 6 1t t   在[1，3]递减， 可得 t＝3 即 x0＝5 时，|BC|＝|m﹣n|取得最小值 2 35 3 ． 【点睛】 本题主要考查了抛物线的定义、标准方程及性质，以及直线与抛物线的位置关系的应用， 其中解答中注意韦达定理和二次函数的单调性的应用是解答的关键，着重考查了分析问 题和解答问题的能力，属于中档试题． 22．已知函数   10 1 axf x lnx x    ． （1）当 a∈R 时，讨论函数 f（x）的单调性； （2）对任意的 x∈（1，+∞）均有 f（x）＜ax，若 a∈Z，求 a 的最小值． 【答案】（1）答案不唯一，具体见解析（2）a 的最小值为 3 【解析】（1）求得函数的导数    2 2 10 20 10 ( 1) x a xf x x x      ，令    210 20 10g x x a x    ，分情况讨论 a ，进而可得求得函数  f x 的单调性； （2）由  f x ax 得到 2 10ln 1 axx x   ，转化为   2 10 1x lnxa x  ，对任意 (1, )x  成 立，令     2 10 1x lnxF x x  ，利用导数求得函数  F x 的最大值，即可求得实数 a 的 第 21 页 共 22 页 最小值． 【详解】 （1）由题意，函数   10 1 axf x lnx x    ， 则    2 2 2 10 20 1010 ( 1) ( 1) x a xaf x x x x x        ，x＞0 且 x≠1， 令    210 20 10g x x a x    ，则其图象对称轴为直线 x 20 20 a ，g（0）＝10， 当 20 020 a  ，即 a≥20 时，则 g（x）＞0，f′（x）＞0， 此时 f（x）分别在（0，1）和（1，+∞）上递增， 当 20 020 a  时，即 a＜20 时，令△＝（a﹣20）2﹣400≤0．可得 0≤a＜20， 所以当 0≤a＜20 时，则 g（x）＞0，f′（x）＞0， 此时 f（x）分别在（0，1）和（1，+∞）上递增， 当 a＜0 时，由 g（x）＝0 解得 x1 220 40 20 a a a   ，x2 220 40 20 a a a   ， 易知 f（x）分别在（0，x1），（x2，+∞）上递增，分别在（x1，1），（1，x2）上递减． 综上所述，当 a≥0 时，f（x）分别在（0，1）和（1，+∞）上递增， 当 a＜0 时，分别在（0，x1），（x2，+∞）上递增，分别在（x1，1），（1，x2）上递减． （2）由题意得， 2 10ln 1 1 ax axx axx x     ， 即   2 10 1x lnxa x  ，对任意 (1, )x  成立， 令 F（x）   2 10 1x lnx x  ，x＞1，则   3( ) 10 2 1x lnF x x x x       ，x＞1， 令 h（x）＝（2﹣x）lnx+x﹣1，h′（x）＝﹣lnx 2 x  ，x＞1 因为 h′（x）在（1，+∞）上递减，且 h′（1）＝2＞0，当 x→+∞时，h′（x）→﹣∞， 所以存在 x0∈（1，+∞），使得 h′（x0）＝0，且 h（x）在（1，x0）上递增，在（x0，+∞） 上递减， 因为 h（1）＝0，所以 h（x0）＞0， 因为当 x→+∞时，h（x）→﹣∞，所以存在 x1∈（x0，+∞），使得 h（x1）＝0， 且 F（x）在（1，x1）上递增，在（x1，+∞）上递减， 第 22 页 共 22 页 所以 F（x）max＝F（x1）  1 1 2 1 10 1x lnx x  ， 因为 h（x1）＝（2﹣x1）lnx1+x1﹣1＝0，所以 lnx1 1 1 1 2 x x   ，所以 F（x1）   2 1 2 1 1 10( 1) 2 x x x   ， 因为 h（4）＝﹣2ln4+3＝ln 3 16 e  0，h（5）＝﹣3ln5+4＝ln 4 35 e  0，所以 x1∈[4，5]， 令Φ（x）   2 2 10( 1) 2 x x x   ，x∈[4，5]，易证Φ（x）在区间[4，5]上递减， 所以Φ（x）∈[ 32 15 ， 45 16 ]， 即 F（x）max∈[ 32 15 ， 45 16 ]，因为 a∈Z，所以 a 的最小值为 3． 【点睛】 本题主要考查导数在函数中的综合应用，以及恒成立问题的求解，着重考查了转化与化 归思想、逻辑推理能力与计算能力，对于恒成立问题，通常要构造新函数，利用导数研 究函数的单调性，求出最值，进而得出相应的含参不等式，从而求出参数的取值范围； 也可分离变量，构造新函数，直接把问题转化为函数的最值问题．