高中数学人教a版选修1-2课时跟踪检测（二）独立性检验的基本思想及其初步应用word版含解析 5页

课时跟踪检测(二) 独立性检验的基本思想及其初步应用 一、选择题 1．判断两个分类变量是彼此相关还是相互独立的常用的方法中，最为精确的是( ) A．2×2 列联表 B．独立性检验 C．等高条形图 D．其他 解析：选 B A、C 只能直观地看出两个分类变量 x 与 y 是否相关，但看不出相关的程度．独 立性检验通过计算得出相关的可能性，较为准确． 2．对于分类变量 X 与 Y 的随机变量 K2 的观测值 k，下列说法正确的是( ) A．k 越大，“X 与 Y 有关系”的可信程度越小 B．k 越小，“X 与 Y 有关系”的可信程度越小 C．k 越接近于 0，“X 与 Y 没有关系”的可信程度越小 D．k 越大，“X 与 Y 没有关系”的可信程度越大 解析：选 B k 越大，“X 与 Y 没有关系”的可信程度越小，则“X 与 Y 有关系”的可信 程度越大．即 k 越小，“X 与 Y 有关系”的可信程度越小．故选 B. 3．利用独立性检验对两个分类变量是否有关系进行研究时，若在犯错误的概率不超过 0.005 的前提下认为事件 A 和 B 有关系，则具体计算出的数据应该是( ) A．k≥6.635 B．k＜6.635 C．k≥7.879 D．k＜7.879 解析：选 C 犯错误的概率为 0.5%，对应的 k0 的值为 7.879，由独立性检验的思想可知 应为 k≥7.879. 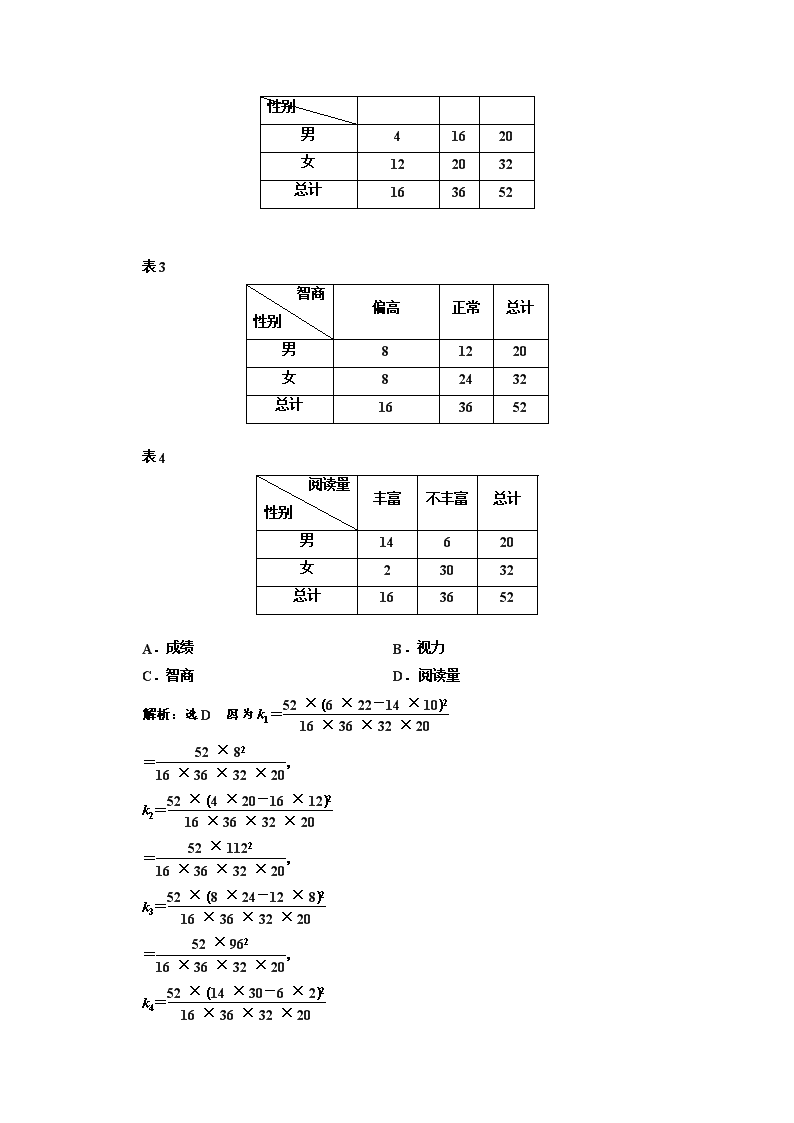4．(江西高考)某人研究中学生的性别与成绩、视力、智商、阅读量这 4 个变量的关系， 随机抽查了 52 名中学生，得到统计数据如表 1 至表 4，则与性别有关联的可能性最大的变量 是( ) 表 1 成绩 性别 不及格 及格 总计 男 6 14 20 女 10 22 32 总计 16 36 52 表 2 视力 好 差 总计 性别 男 4 16 20 女 12 20 32 总计 16 36 52 表 3 智商 性别 偏高 正常 总计 男 8 12 20 女 8 24 32 总计 16 36 52 表 4 阅读量 性别 丰富 不丰富 总计 男 14 6 20 女 2 30 32 总计 16 36 52 A．成绩 B．视力 C．智商 D．阅读量 解析：选 D 因为 k1＝52×6×22－14×102 16×36×32×20 ＝ 52×82 16×36×32×20 ， k2＝52×4×20－16×122 16×36×32×20 ＝ 52×1122 16×36×32×20 ， k3＝52×8×24－12×82 16×36×32×20 ＝ 52×962 16×36×32×20 ， k4＝52×14×30－6×22 16×36×32×20 ＝ 52×4082 16×36×32×20 ， 则有 k4>k2>k3>k1， 所以阅读量与性别关联的可能性最大. 5．通过随机询问 110 名性别不同的大学生是否爱好某项运动，得到如下的列联表： 男 女 总计 爱好 40 20 60 不爱好 20 30 50 总计 60 50 110 由 K2＝ nad－bc2 a＋bc＋da＋cb＋d 算得，观测值 k＝110×40×30－20×202 60×50×60×50 ≈7.8. 附表： P(K2≥k0) 0.050 0.010 0.001 k0 3.841 6.635 10.828 参照附表，得到的正确结论是( ) A．有 99%以上的把握认为“爱好该项运动与性别有关” B．有 99%以上的把握认为“爱好该项运动与性别无关” C．在犯错误的概率不超过 0.1%的前提下，认为“爱好该项运动与性别有关” D．在犯错误的概率不超过 0.1%的前提下，认为“爱好该项运动与性别无关” 解析：选 A 由 k≈7.8 及 P(K2≥6.635)＝0.010 可知，在犯错误的概率不超过 1%的前提 下认为“爱好该项运动与性别有关”，也就是有 99%以上的把握认为“爱好该项运动与性别 有关”． 二、填空题 6．下列关于 K2 的说法中，正确的有________(填序号)． ①K2 的值越大，两个分类变量的相关性越大； ②K2 的计算公式是 K2＝ nad－bc a＋bc＋da＋cb＋d ； ③若求出 K2＝4＞3.841，则有 95%的把握认为两个分类变量有关系，即有 5%的可能性 使得“两个分类变量有关系”的推断出现错误； ④独立性检验就是选取一个假设 H0条件下的小概率事件，若在一次试验中该事件发生了， 这是与实际推断相抵触的“不合理”现象，则作出拒绝 H0 的推断． 解析：对于①，K2 的值越大，只能说明我们有更大的把握认为二者有关系，却不能判断 相关性大小，故①错；对于②，(ad－bc)应为(ad－bc)2，故②错；③④对． 答案：③④ 7．某电视台在一次对收看文艺节目和新闻节目观众的抽样调查中，随机抽取了 100 名电 视观众，相关的数据如下表所示： 文艺节目 新闻节目 总计 20 至 40 岁 40 18 58 大于 40 岁 15 27 42 总计 55 45 100 由表中数据直观分析，收看新闻节目的观众是否与年龄有关：________(填“是”或 “否”)． 解析：因为在 20 至 40 岁的 58 名观众中有 18 名观众收看新闻节目，而大于 40 岁的 42 名观众中有 27 名观众收看新闻节目，即 b a＋b ＝18 58 ， d c＋d ＝27 42 ，两者相差较大，所以经直观分 析，收看新闻节目的观众与年龄是有关的． 答案：是 8．某工厂为了调查工人文化程度与月收入的关系，随机抽取了部分工人，得到如下列联 表： 文化程度与月收入列联表 (单位：人) 月收入 2 000 元以下 月收入 2 000 元 及以上 总计 高中文化以上 10 45 55 高中文化及以下 20 30 50 总计 30 75 105 由上表中数据计算得 K2 的观测值 k＝105×10×30－45×202 55×50×30×75 ≈6.109，请估计有________ 把握认为文化程度与月收入有关系． 解析：由于 6.109＞5.024，所以在犯错误的概率不超过 0.025 的前提下，即有 97.5%的把 握认为文化程度与月收入有关系． 答案：97.5% 三、解答题 9．巴西医生马廷恩收集犯有各种贪污、受贿罪的官员与廉洁官员寿命的调查资料：500 名贪官中有 348 人的寿命小于平均寿命，152 人的寿命大于或等于平均寿命；590 名廉洁官员 中有 93 人的寿命小于平均寿命，497 人的寿命大于或等于平均寿命．这里，平均寿命是指“当 地人均寿命”．能否在犯错误的概率不超过 0.01 的前提下认为官员在经济上是否清廉与他们 寿命的长短之间有关系？ 解：据题意列 2×2 列联表如下： 短寿(B) 长寿( B－) 总计 贪官(A) 348 152 500 廉洁官( A－) 93 497 590 总计 441 649 1 090 假设官员是否清廉与他们寿命的长短无关． 由公式得 K2 的观测值 k＝1 090×348×497－152×932 500×590×441×649 ≈325.635. 因为 325.635＞6.635，因此，在犯错误的概率不超过 0.01 的前提下认为官员在经济上是 否清廉与他们寿命的长短之间是有关系的． 10．某地震观测站对地下水位的变化和发生地震的情况共进行 1 700 次观测，列联表如下： 有震 无震 总计 水位有变化 98 902 1 000 水位无变化 82 618 700 总计 180 1 520 1 700 利用图形判断地下水位的变化与地震的发生是否有关系，并用独立性检验分析是否有充 分的证据显示二者有关系． 解：相应的等高条形图如图所示． 图中两个阴影条的高分别表示水位有变化和水位无变化的样本中有震的频率．由图可看 出，水位有变化样本中有震的频率与水位无变化样本中有震的频率相差不大，因此不能判断 地震与水位变化有关系． 根据列联表中的数据，得 K2 的观测值为 k＝1 700×98×618－902×822 1 000×700×180×1 520 ≈1.594<2.072， 所以题中数据没有充分的证据显示地下水位的变化与地震的发生有关系，但也不能认为 二者无关系．