人教A版高中数学2-1-2指数函数（1）教案新人教版必修1 4页

2.1.1（1）指数函数（教学设计） 教学目标 1. 理解指数函数的定义,初步掌握指数函数的图象,性质及其简单应用. 2. 通过指数函数的图象和性质的学习,培养学生观察,分析,归纳的能力,进一步体会数形结合的思想方法. 3. 通过对指数函数的研究,使学生能把握函数研究的基本方法,激发学生的学习兴趣. 教学重点和难点 重点是理解指数函数的定义,把握图象和性质. 难点是认识底数对函数值影响的认识. 教学过程 一、复习回顾，新课引入 问题 1:某种细胞分裂时,由 1 个分裂成 2 个,2 个分裂成 4 个,……一个这样的细胞分裂 次后,得到的细胞分裂的 个数 与 之间,构成一个函数关系,能写出 与 之间的函数关系式吗? 由学生回答: 与 之间的关系式,可以表示为 . 问题 2:有一根 1 米长的绳子,第一次剪去绳长一半,第二次再剪去剩余绳子的一半,……剪了 次后绳子剩余的长 度为 米,试写出 与 之间的函数关系. 由学生回答: . 在以上两个实例中我们可以看到这两个函数与我们前面研究的函数有所区别,从形式上幂的形式,且自变量 均在 指数的位置上,那么就把形如这样的函数称为指数函数. 二、师生互动，新课讲解： 1.定义:形如 的函数称为指数函数. 2.几点说明 (1) 关于对 的规定: 教师首先提出问题:为什么要规定底数大于 0 且不等于 1 呢?(若学生感到有困难,可将问题分解为若 会有什 么问题?如 ,此时 , 等在实数范围内相应的函数值不存在. 若 xa 对于 都无意义,若 则 无论 取何值,它总是 1,对它没有研究的必要.为了避免上述各种情 况的发生,所以规定 且 . (2)关于指数函数的定义域 教师引导学生回顾指数范围,发现指数可以取有理数.此时教师可指出,其实当指数为无理数时, 也是一个确定 的实数,对于无理指数幂,学过的有理指数幂的性质和运算法则它都适用,所以将指数范围扩充为实数范围,所以指数函 数的定义域为 .扩充的另一个原因是因为使她它更具代表更有应用价值. (3)关于是否是指数函数的判断 学生课堂练习 1：根据指数函数的定义判断下面函数是否是指数函数. (1) , (2) , (3) (4) , (5) . 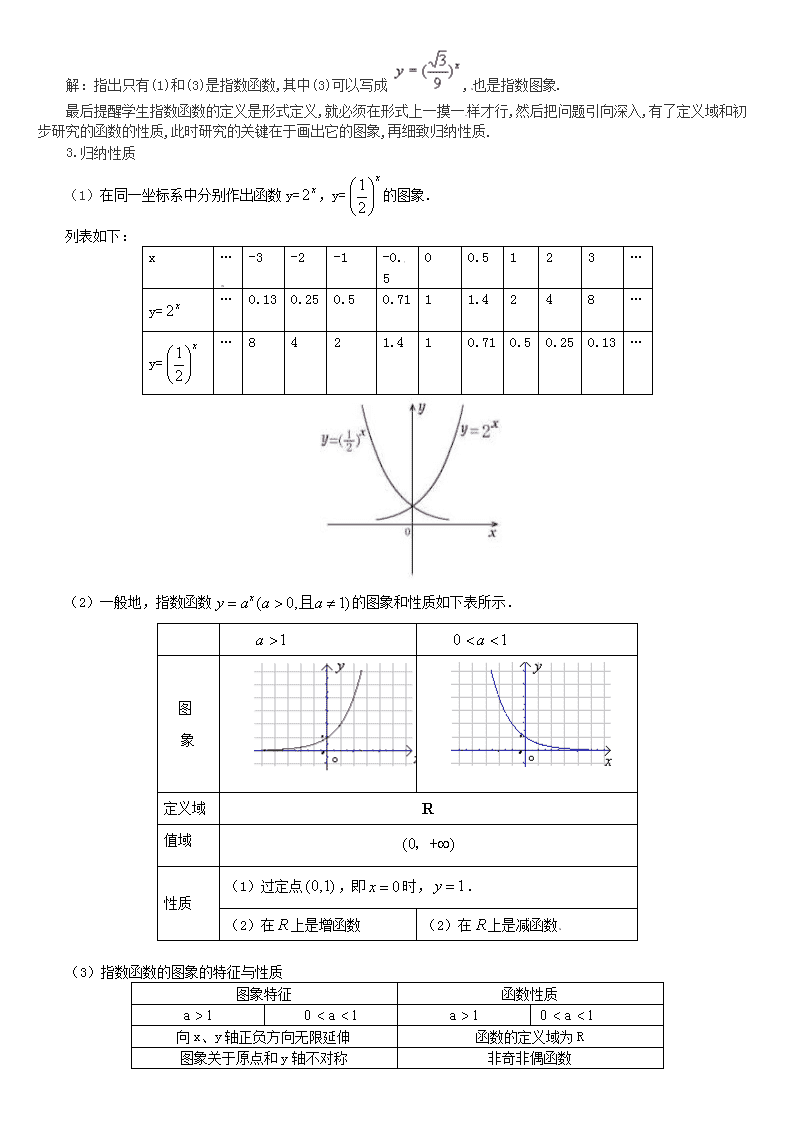解：指出只有(1)和(3)是指数函数,其中(3)可以写成 ,也是指数图象. 最后提醒学生指数函数的定义是形式定义,就必须在形式上一摸一样才行,然后把问题引向深入,有了定义域和初 步研究的函数的性质,此时研究的关键在于画出它的图象,再细致归纳性质. 3.归纳性质 （1）在同一坐标系中分别作出函数 y= x2 ，y= x      2 1 的图象. 列表如下： x … -3 -2 -1 -0. 5 0 0.5 1 2 3 … y= x2 … 0.13 0.25 0.5 0.71 1 1.4 2 4 8 … y= x      2 1 … 8 4 2 1.4 1 0.71 0.5 0.25 0.13 … （2）一般地，指数函数 ( 0, 1)xy a a a  且 的图象和性质如下表所示． 1a  0 1a  图 象 定义域 R 值域 (0 )，+ 性质 （1）过定点 (0,1) ，即 0x  时， 1y  ． （2）在 R 上是增函数 （2）在 R 上是减函数 （3）指数函数的图象的特征与性质 图象特征 函数性质 1a  1a0  1a  1a0  向 x、y 轴正负方向无限延伸 函数的定义域为 R 图象关于原点和 y 轴不对称 非奇非偶函数 函数图象都在 x 轴上方 函数的值域为 R+ 函数图象都过定点（0，1） 1a 0  自左向右看， 图象逐渐上升 自左向右看， 图象逐渐下降 增函数 减函数 在第一象限内的图 象纵坐标都大于 1 在第一象限内的图 象纵坐标都小于 1 1a,0x x  1a,0x x  在第二象限内的图 象纵坐标都小于 1 在第二象限内的图 象纵坐标都大于 1 1a,0x x  1a,0x x  图象上升趋势是越 来越陡 图象上升趋势是越 来越缓 函数值开始增长较 慢，到了某一值后 增长速度极快； 函数值开始减小极 快，到了某一值后 减小速度较慢； 例 1（课本 P56 例 6）：已知指数函数 ( 0, 1)xy a a a  且 的图象经过点（3，），求 )0(f ， )1(f ， )3(f 的值． 例 2（课本 P57 例 7）：比较下列各题中两个值的大小： （1） 35.2 7.1,7.1 （2） 2.01.0 8.0,8.0  （3）1.70.3，0.93.1 解：利用函数单调性 ① 5.27.1 与 37.1 的底数是 1.7，它们可以看成函数 y= x7.1 ，当 x=1.7 和 3 时的函数值；因为 1.7>1，所以函数 y= x7.1 在 R 是增函数，而 2.5<3，所以， 5.27.1 < 37.1 ； ② 1.08.0  与 2.08.0  的底数是 0.8，它们可以看成函数 y= x8.0 ，当 x=-0.1 和-0.2 时的函数值；因为 0<0.8<1，所 以函数 y= x8.0 在 R 是减函数，而-0.1>-0.2，所以， 1.08.0  < 2.08.0  ； ③在下面个数之间的横线上填上适当的不等号或等号： 3.07.1 >1； 1.39.0 <1； 3.07.1 > 1.39.0 小结：对同底数幂大小的比较用的是指数函数的单调性，必须要明确所给的两个值是哪个指数函数的两个函数值； 对不同底数是幂的大小的比较可以与中间值进行比较. 变式训练 2： （1）比较下列各组数的大小 1) 与 ; 2) 与 ; 3) 与 1 ；4) 与 解: 在 上是增函数,且 < . ⑵已知下列不等式，试比较 m、n 的大小： （1） nm )3 2()3 2(  ；（2） nm 1.11.1  . 三、课堂小结，巩固反思： 1、理解并掌握指数函数的图像与性质。 2、会根据指数函数的单调性比较两个数（式）的大小。 四、布置作业： A 组： 1、(tb0113301)下列函数中为指数函数的是（C）。 （A）形如 y=ax 的函数 （B）y=xa (a>0 且 a  1) （C）y=(|a|+2) –x (D) y=3ax (a>0 且 a  1) 2、(tb0113701)下列结论中正确的是（C）。 （A） 任何指数函数都是增函数 （B）有确定底数的指数函数可能是增函数，也可能是减函数 （C） 所有的指数函数都是单调函数 （D）有的指数函数是单调函数，有的指数函数不是单调函数 3、(tb0113702)已知 a=0.80.7，b=0.8 0.9，c=1.2 0.8，则 a,b,c 的大小关系是（A）。 （A）c>a>b (B) c>b>a (C)a>b>c (D)b>a>c 4． 若函数 y＝(a2－1)x 在(－∞，＋∞)上为减函数，则实数 a 的取值范围是__________． 答案 (－ 2，－1)∪(1， 2) 解析 由 y＝(a2－1)x 在(－∞，＋∞)上为减函数，得 00，a≠1)的图象恒过定点 A(其 坐标与 a 无关)，则定点 A 的坐标为__________． 解析：当 x＝－2 时，无论 a 取何值，都有 y＝－1，即图象恒过定点 A(－2，－1)． 答案：(－2，－1) 2． 作出函数 | 1|2 xy  的图像，并写出它的单调区间。（提示： | 1|2 xy  由 | |2 xy  向右平移一个单位而得）