江苏省泰州市2020～2021学年度第一学期期中调研测试高三数学 13页

泰州2020～2021学年度第一学期期中调研测试 高三数学试题 ‎(考试时间：120分钟；总分：150分)‎ 一、选择题：（本题共8小题，每小题5分，共40分，在每小题给出的四个选项中，只有一项符合题目要求，请将答案填涂到答题卡相应区域）．‎ ‎1．设集合，集合，则（ ▲ ）‎ A． B． C． D． ‎ ‎2．已知，为虚数单位，则“”是“为纯虚数”的（ ▲ ）‎ A．充分不必要条件 B．必要不充分条件 C．充分必要条件 D．既不充分也不必要条件 ‎3. 欧拉是瑞士著名数学家，他首先发现：（为自然对数的底数，为虚数单位），此结论被称为“欧拉公式”，它将指数函数的定义域扩大到复数集，建立了三角函数和指数函数的关系．根据欧拉公式可知，=（ ▲ ）‎ A. B. 0 C. D. ‎ ‎4. 埃及金字塔是古埃及的帝王（法老）陵墓，世界七大奇迹之一，其中较为著名的是胡夫金字塔．令人吃惊的并不仅仅是胡夫金字塔的雄壮身姿，还有发生在胡夫金字塔上的数字“巧合”．如胡夫金字塔的底部周长除以其两倍的高度，得到的商为3.14159，这就是圆周率较为精确的近似值．金字塔底部形为正方形，整个塔形为正四棱锥，经古代能工巧匠建设完成后，底座边长大约230米．因年久风化，顶端剥落10米，则胡夫金字塔现在的高度大约为（ ▲ ）‎ A．128.4米 B．132.4米 C．136.4米 D．110.4米 ‎5．在平行四边形中，点分别满足，，‎ 高三数学试题 第13页 共6页 若，则实数的值为（ ▲ ）‎ A． B. C. D. 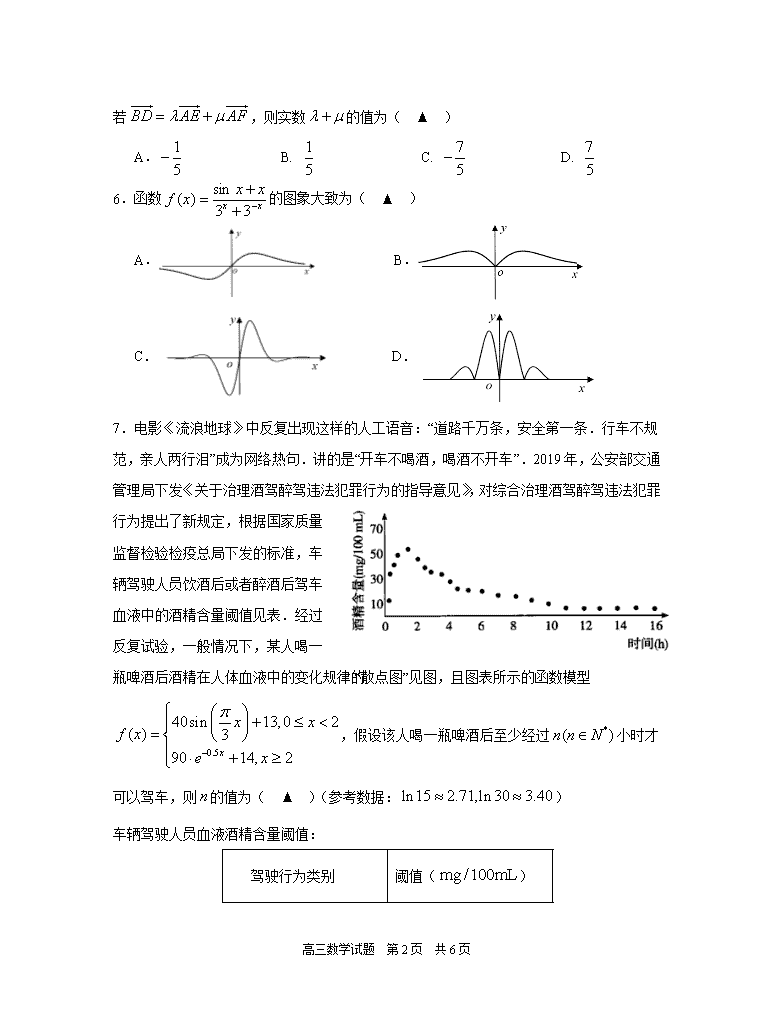‎ ‎6．函数的图象大致为（ ▲ ）‎ A． B．‎ C． D． ‎ ‎7．电影《流浪地球》中反复出现这样的人工语音：“道路千万条，安全第一条．行车不规范，亲人两行泪”成为网络热句．讲的是“开车不喝酒，喝酒不开车”．2019年，公安部交通管理局下发《关于治理酒驾醉驾违法犯罪行为的指导意见》，对综合治理酒驾醉驾违法犯罪行为提出了新规定，根据国家质量监督检验检疫总局下发的标准，车辆驾驶人员饮酒后或者醉酒后驾车血液中的酒精含量阈值见表．经过反复试验，一般情况下，某人喝一瓶啤酒后酒精在人体血液中的变化规律的“散点图”见图，且图表所示的函数模型，假设该人喝一瓶啤酒后至少经过小时才 可以驾车，则的值为（ ▲ ）（参考数据：）‎ 车辆驾驶人员血液酒精含量阈值：‎ 驾驶行为类别 阈值（）‎ 高三数学试题 第13页 共6页 饮酒驾车 ‎［20，80）‎ 醉酒驾车 ‎［80，+∞）‎ A．5 B．6 C．7 D．8‎ ‎8．若实数满足其中，则下列结论正确的是（ ▲ ）‎ A. B. C. D. ‎ 二、选择题：本题共4小题，每小题5分，共20分.在每小题给出的选项中，有多项符合题目要求.全部选对的得5分，有选错的得0分，部分选对的得3分.‎ ‎9. 已知向量，则下列选项正确的有（ ▲ ） ‎ A． B． ‎ C． D． ‎ ‎10. 已知函数的导函数的两个零点为，则下列结论正确的有（ ▲ ） ‎ A. B. 在区间的最大值为 ‎ C.只有一个零点 D. 的极大值是正数 ‎11. 某港口一天内潮水的高度（单位：）随时间（单位：；）的变化近似满足关系式，则下列说法正确的有（ ▲ ）‎ A．在上的平均变化率为 B．相邻两次潮水高度最高的时间间距为 C．当时，潮水的高度会达到一天中最低 D．时潮水起落的速度为 ‎12. 在棱长为的正方体中，点是棱的中点，点是底面 高三数学试题 第13页 共6页 上的动点，且，则下列说法正确的有（ ▲ ） ‎ A. 与所成角的最大值为 B. 四面体的体积不变 ‎ C. 的面积有最小值 D. 平面截正方体所得截面面积不变 ‎ 三、填空题：（本题共4小题，每题5分，共20分，请将答案填写在答题卡相应的位置上）.‎ ‎13．已知，则的值为 ▲ ．‎ ‎14．乒乓球被称为中国的“国球”，目前国际比赛用球的直径为4．某厂家计划生产乒 乓球包装盒，包装盒为长方体，每盒装6个乒乓球．现有两种方案，方案甲：6个乒乓球 放一排；方案乙： 6个乒乓球并排放置两排，每排放3个．乒乓球与盒子、以及乒乓球之间紧密接触，确保用料最省，则方案甲中包装盒的表面积比方案乙中包装盒的表面积多 ‎ ▲ ．‎ ‎15．已知正实数满足，则的最小值为 ▲ ．‎ ‎16. 已知直三棱柱中，，，侧棱，则该三棱柱外接球的体积为 ▲ ．‎ 三、解答题：（本大题共6小题，共70分．解答应写出文字说明，证明过程或演算步骤．）‎ ‎17．（本题满分10分）‎ 设集合，.‎ ‎（1）当时，求；‎ ‎（2）若，求实数的取值范围.‎ 高三数学试题 第13页 共6页 ‎18．（本题满分12分）‎ 已知向量，，函数.‎ ‎（1）求函数的单调递增区间；‎ ‎（2）求函数在区间上的最大值和最小值，并求出相应的的值.‎ ‎19．（本题满分12分）‎ 已知的内角所对的边分别是，为锐角，在以下三个条件中任选一个：①；②；‎ ③；并解答以下问题：‎ ‎（1）若选______（填序号），求的值；‎ ‎（2）在（1）的条件下，若，求面积的最大值．‎ ‎20．（本题满分12分）‎ 如图，在四棱锥中，，，为正三角形，是CB的中点，，．‎ ‎（1）求证：平面平面；‎ ‎（2）求二面角的余弦值；‎ ‎（3）求四棱锥的体积．‎ 高三数学试题 第13页 共6页 ‎21．（本题满分12分）‎ 已知函数，．‎ ‎（1）解不等式：；‎ ‎（2）当时，求函数的值域；‎ ‎（3）若，，使得成立，求实数的取值范围．‎ ‎22．（本题满分12分）‎ ‎ 已知函数，．‎ ‎（1）求函数的最小值；‎ ‎（2）若是的切线，求实数的值；‎ ‎（3）若与的图象有两个不同交点，求证：．‎ 高三数学试题 第13页 共6页 高三数学试题 第13页 共6页 ‎2020～2021学年度第一学期期中调研测试 高三数学试题参考答案 一、单项选择题： ‎ ‎1．A 2．B 3. C 4. C 5．B 6．A 7．B 8．D 二、多项选择题： ‎ ‎9. ABD 10. BC 11. BD 12. BCD ‎ 三、填空题： ‎ ‎13． 14.64 15． 16.‎ 三、解答题： ‎ ‎17．（本题满分10分）‎ 解：-------------------------2分 ‎ ‎ ‎（1）当时，--------------------------------------4分 所以 -----------------------------------------6分 ‎（2）因为，所以，有：‎ ‎，解得：， ‎ 所以实数的取值范围为.-----------------------------------------10分 ‎18．（本题满分12分）‎ 解:(1)‎ ‎ ‎ ‎ ‎ ‎ -------------------------------------4分 高三数学试题 第13页 共6页 由， ‎ 解得：，‎ 所以函数的单调递增区间为：.--------6分 ‎（2）因为，所以，---------------------8分 所以，即，--------------10分 当时，有最大值为0;‎ 当时, 有最小值为.----------------------------12分 ‎19．（本题满分12分）‎ 解：（1）若选①，因为，由正弦定理有：‎ ‎ ,‎ 即，‎ ‎ 所以，在中，，所以.--------6分 若选②, ，‎ ‎，‎ 中，,，‎ ‎，,‎ ‎，或（舍）, .---------------------6分 若选③，因为，由正弦定理有：‎ ‎ ，因为在中，，所以，‎ ‎ 又，为锐角，解得.------------------------6分 高三数学试题 第13页 共6页 ‎（2）由（1）可知， ，由，为锐角，得，‎ 由余弦定理可知，‎ ‎，‎ ‎，当且仅当时等号成立.---------------------------9分 面积：.‎ 所以面积的最大值为.------------------------------12分 ‎20．（本题满分12分）‎ 解：（1）因为为正三角形，是CB的中点，‎ 所以，‎ 因为，，平面，平面，‎ 所以平面，‎ 因为平面 所以平面平面．----------------------------------4分 ‎（2）由（1）中平面，则，‎ 又，所以是二面角的平面角，‎ 因为，，所以，，‎ 因为，，‎ 所以，‎ 即二面角的余弦值为．-------------------------------8分 ‎（3）在中，过作于，‎ 高三数学试题 第13页 共6页 由（1）中得平面，又因为平面，‎ 所以平面平面，‎ 又平面，‎ 故平面，-------------------------------10分 由为正三角形，得的面积，‎ 的面积，四边形的面积为 在中，‎ 所以四棱锥的体积．‎ ‎----------------------------------------------------------------------------------------------------12分 ‎21．（本题满分12分）‎ 解：（1）由得，‎ 即，‎ 所以，又 所以，即不等式的解集为；-------------------------3分 ‎（2），‎ ①当时，；‎ ②当时，，‎ 令，则，，‎ 即在上为减函数，故；‎ 综上得：当时，函数的值域为；-----------------------------------7分 高三数学试题 第13页 共6页 ‎（3）由题意得，，，‎ 当，由（2）得，所以，‎ 所以恒成立，‎ 即恒成立，------------------------------------------------10分 又，当且仅当时取等号，‎ 所以实数的取值范围为．----------------------------------12分 ‎22．（本题满分12分）‎ 解：（1）∵，∴，‎ 当时，，∴在上单调递减；‎ 当时，，∴在上单调递增．‎ 故函数的最小值为．--------------3分 ‎（2）若是的切线，设切点为，‎ 则过点的切线方程为，‎ 即，即，‎ 由题意知，----------------------------------------5分 高三数学试题 第13页 共6页 令，则时，，‎ ‎∴在上单调递增，又，‎ ‎∴有唯一的实根，则．----7分 ‎（3）由题意知，‎ 两式相加得，‎ 两式相减得，即，‎ ‎∴，即，‎ 不妨令，记，则，‎ 令，则，‎ ‎ ∴在上单调递增，则，‎ ‎∴，因而，‎ 令，则时，，∴在上单调递增，‎ ‎∵，∴．--------------------12分 高三数学试题 第13页 共6页