高中人教a版数学必修1单元测试：第三章函数的应用a卷word版含解析 13页

高中同步创优单元测评 A 卷 数 学 班级：________ 姓名：________ 得分：________ 第三章 函数的应用 名师原创·基础卷] (时间：120 分钟 满分：150 分) 第Ⅰ卷 (选择题 共 60 分) 一、选择题(本大题共 12 个小题，每小题 5 分，共 60 分，在每小 题给出的四个选项中，只有一项是符合题目要求的) 1．函数 y＝x2－2x－3 的零点是( ) A．1，－3 B．3，－1 C．1,2 D．不存在 2．用二分法求方程 f(x)＝0 在区间(1,2)内的唯一实数解 x0 时，经 计算得 f(1)＝ 3，f(2)＝－5，f 3 2 ＝9，则下列结论正确的是( ) A．x0∈ 1，3 2 B．x0＝3 2 C．x0∈ 3 2 ，2 D．x0∈ 1，3 2 或 x0∈ 3 2 ，2 3．若函数 f(x)＝ax＋b 的零点是－1(a≠0)，则函数 g(x)＝ax2＋bx 的零点是( ) A．－1 B．0 C．－1 和 0 D．1 和 0 4．某种型号的手机自投放市场以来，经过两次降价，单价由原来 的 2 000 元降到 1 280 元，则这种手机的价格平均每次降低的百分率是 ( ) A．10% B．15% C．18% D．20% 5．设函数 f(x)＝ x2＋bx＋c，x≤0， 3，x>0， 若 f(－4)＝f(0)，f(－2)＝－2， 则函数 y＝f(x)－x 的零点的个数为( ) A．1 B．2 C．3 D．4 6．函数 f(x)＝ln(x＋1)－2 x 的零点所在的大致区间是( ) A．(0,1) B．(1,2) C．(2，e) D．(3,4) 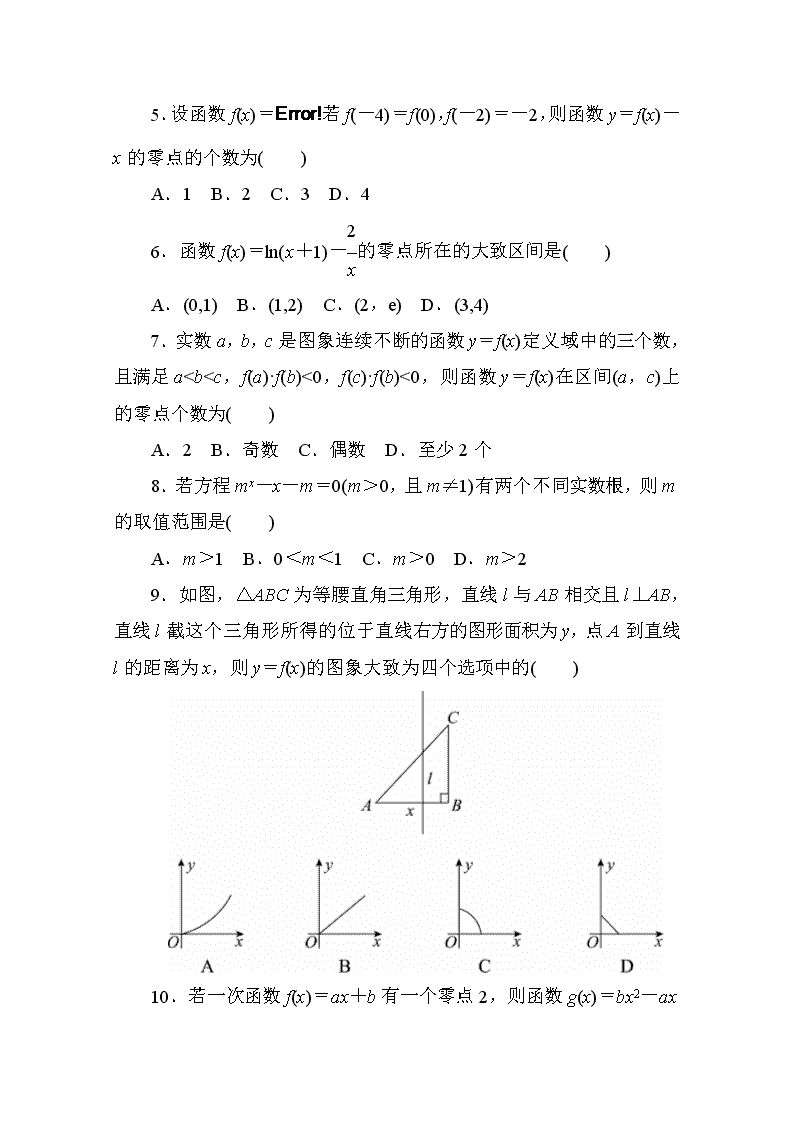7．实数 a，b，c 是图象连续不断的函数 y＝f(x)定义域中的三个数， 且满足 a0， －x2－2x，x≤0， 若函数 g(x)＝f(x)－m 有 3 个零点，则实数 m 的取值范围是________． 三、解答题(本大题共 6 个小题，共 70 分，解答时应写出必要的文 字说明、证明过程或演算步骤) 17．(本小题满分 10 分) 若二次函数 f(x)＝－x2＋2ax＋4a＋1 有一个零点小于－1，一个零 点大于 3，求实数 a 的取值范围． 18．(本小题满分 12 分) 已知二次函数 f(x)的图象过点(0,3)，它的图象的对称轴为 x＝2，且 f(x)的两个零点的平方和为 10，求 f(x)的解析式． 19．(本小题满分 12 分) 某公司制定了一个激励销售人员的奖励方案：当销售利润不超过 10 万元时，按销售利润的 15%进行奖励；当销售利润超过 10 万元时， 若超出 A 万元，则超出部分按 2log5(A＋1)进行奖励．记奖金为 y(单位： 万元)，销售利润为 x(单位：万元)． (1)写出该公司激励销售人员的奖励方案的函数模型； (2)如果业务员老江获得 5.5 万元的奖金，那么他的销售利润是多 少万元？ 20．(本小题满分 12 分) 设函数 f(x)＝ax2＋(b－8)x－a－ab 的两个零点分别是－3 和 2. (1)求 f(x)； (2)当函数 f(x)的定义域是 0,1]时，求函数 f(x)的值域． 21．(本小题满分 12 分) 函数 y＝f(x)的图象关于 x＝1 对称，当 x≤1 时，f(x)＝x2－1. (1)写出 y＝f(x)的解析式并作出图象； (2)根据图象讨论 f(x)－a＝0(a∈R)的根的情况． 22．(本小题满分 12 分) 某家庭进行理财投资，根据长期收益率市场预测，投资债券等稳 健型产品的收益与投资额成正比，投资股票等风险型产品的收益与投 资额的算术平方根成正比．已知投资 1 万元时两类产品的收益分别为 0.125 万元和 0.5 万元(如图)． (1)分别写出两种产品的收益与投资的函数关系； (2)该家庭有 20 万元资金，全部用于理财投资，问：怎么分配资金 能使投资获得最大收益，其最大收益是多少万元？ 详解答案 第三章 函数的应用 名师原创·基础卷] 1．B 解析：令 x2－2x－3＝0 得 x＝－1 或 x＝3，故选 B. 2．C 解析：∵f(2)·f 3 2 <0，∴x0∈ 3 2 ，2 . 3．C 解析：由条件知 f(－1)＝0，∴b＝a，∴g(x)＝ax2＋bx＝ax(x ＋1)的零点为 0 和－1，故选 C. 4．D 解析：由题意，可设平均每次价格降低的百分率为 x， 则有 2 000(1－x)2＝1 280， 解得 x＝0.2 或 x＝1.8(舍去)，故选 D. 5．C 解析：本题主要考查二次函数、分段函数及函数的零点．f(－ 4)＝f(0)⇒b＝4，f(－2)＝－2⇒c＝2，∴ f(x)＝ x2＋4x＋2，x≤0， 3，x>0. 当 x≤0 时，由 x2＋4x＋2＝x 解得 x1＝－1，x2＝－2；当 x>0 时，x＝3.所 以函数 y＝f(x)－x 的零点的个数为 3，故选 C. 6．B 解析：f(1)＝ln(1＋1)－2 1 ＝ln 2－2＝ln 2－ln e2<0，f(2)＝ln(2 ＋1)－2 2 ＝ln 3－1>0，因此函数的零点必在区间(1,2)内，故选 B. 7．D 解析：由 f(a)·f(b)<0 知，y＝f(x)在(a，b)上至少有一零点， 由 f(c)·f(b)<0 知，y＝f(x)在(b，c)上至少有一零点，故 y＝f(x)在(a，c) 上至少有 2 个零点． 8．A 解析：方程 mx－x－m＝0 有两个不同实数根，等价于函数 y＝mx 与 y＝x＋m 的图象有两个不同的交点．显然当 m＞1 时，如图① 有两个不同交点；当 0＜m＜1 时，如图②有且仅有一个交点，故选 A. 9．C 解析：设 AB＝a，则 y＝1 2a2－1 2x2＝－1 2x2＋1 2a2，其图象为 抛物线的一段，开口向下，顶点在 y 轴正半轴．故选 C. 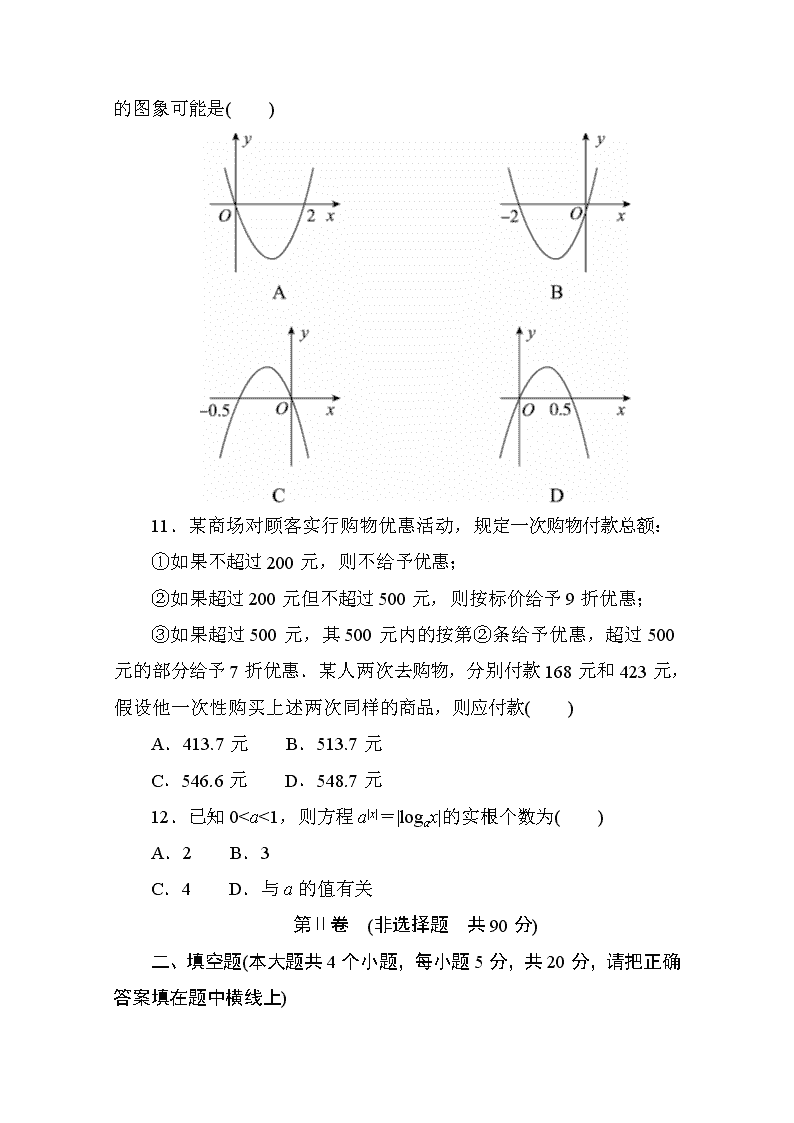10．C 解析：由题意知，2a＋b＝0，所以 a＝－b 2. 因此 g(x)＝bx2＋b 2x＝b x2＋1 2x ＝b x＋1 4 2－ b 16. 易知函数 g(x)图象的对称轴为 x＝－1 4 ，排除 A，D. 又令 g(x)＝0，得 x＝0 或 x＝－0.5，故选 C. 11．C 解析：设该顾客两次购物的商品价格分别为 x，y 元，由 题意可知 x＝168，y×0.9＝423，∴y＝470，故 x＋y＝168＋470＝ 638(元)， 故如果他一次性购买上述两样商品应付款： (638－500)×0.7＋500×0.9＝96.6＋450＝546.6(元)． 12．A 解析：设 y1＝a|x|，y2＝|logax|，分别作出它们的图象如下 图所示． 由图可知，有两个交点，故方程 a|x|＝|logax|有两个根．故选 A. 13．2 解析：由 y＝ln x 与 y＝ 1 x－1 的图象可知有两个交点． 14．3 解析：由表中数据可知，f(1)＝ln 1－1＋2＝1>0， f(2)＝ln 2－2＋2＝ln 2＝0.69>0， f(3)＝ln 3－3＋2＝1.10－1＝0.1>0， f(4)＝ln 4－4＋2＝1.39－2＝－0.61<0， f(5)＝ln 5－5＋2＝1.61－3＝－1.39<0， ∴f(3)·f(4)<0，∴k 的值为 3. 15．9 解析：设乘客每次乘坐出租车需付费用为 f(x)元，由题意， 得 f(x)＝ 8＋1，x∈0，3]， 9＋x－3×2.15，x∈3，8]， 9＋5×2.15＋x－8×2.85，x∈8，＋∞， 令 f(x)＝22.6，显然 9＋5×2.15＋(x－8)×2.85＝22.6(x>8)，解得 x ＝9. 16．(0,1) 解析：画出 f(x)＝ 2x－1，x>0， －x2－2x，x≤0 的图象，如图所示． 由函数 g(x)＝f(x)－m 有 3 个零点，即 f(x)－m＝0 有 3 个不相等的 实根，结合图象，得 00， f3>0， 即 －－12－2a＋4a＋1>0， －32＋2a×3＋4a＋1>0， 即 2a>0， 10a－8>0， 解得 a>4 5. 18．解：设 f(x)＝ax2＋bx＋c(a≠0)， 由题意知，c＝3，－ b 2a ＝2. 设 x1，x2 是方程 ax2＋bx＋c＝0 的两根， 则 x1＋x2＝－b a ，x1·x2＝c a. ∵x21＋x22＝10，∴(x1＋x2)2－2x1x2＝10，即 －b a 2－2c a ＝10，∴42－6 a ＝10， ∴a＝1，b＝－4. ∴f(x)＝x2－4x＋3. 19．解：(1)由题意，得 y＝ 0.15x，010. (2)x∈(0,10]，0.15x≤1.5. 又∵y＝5.5，∴x>10， ∴1.5＋2log5(x－9)＝5.5，∴x＝34. ∴老江的销售利润是 34 万元． 20．解：(1)∵f(x)的两个零点是－3 和 2， ∴函数图象过点(－3,0)，(2,0)， ∴ 9a－3b－8－a－ab＝0，① 4a＋2b－8－a－ab＝0.② ①－②，得 b＝a＋8.③ ③代入②，得 4a＋2a－a－a(a＋8)＝0， 即 a2＋3a＝0. ∵a≠0，∴a＝－3， ∴b＝a＋8＝5. ∴f(x)＝－3x2－3x＋18. (2)由(1)得 f(x)＝－3x2－3x＋18 ＝－3 x＋1 2 2＋3 4 ＋18， 图象的对称轴是 x＝－1 2 ，又 0≤x≤1， ∴f(x)min＝f(1)＝12，f(x)max＝f(0)＝18， ∴函数 f(x)的值域是 12,18]． 21．解：(1)由题意知 f(x)＝ x2－1x≤1， x－22－1x>1. 图象如图所示． (2)当 a<－1 时，f(x)－a＝0 无解； 当 a＝－1 时，f(x)－a＝0 有两个实数根； 当－10 时，f(x)－a＝0 有两个实数根． 22．解：(1)设 f(x)＝k1x，g(x)＝k2 x， 所以 f(1)＝1 8 ＝k1， g(1)＝1 2 ＝k2，即 f(x)＝1 8x(x≥0)，g(x)＝1 2 x(x≥0)． (2)设投资债券类产品 x 万元，则股票类投资为(20－x)万元． 依题意，得 y＝f(x)＋g(20－x) ＝x 8 ＋1 2 20－x(0≤x≤20)． 令 t＝ 20－x(0≤t≤2 5)． 则 y＝20－t2 8 ＋1 2t＝－1 8(t－2)2＋3， 所以当 t＝2，即 x＝16(万元)时，收益最大，最大收益为 3 万元．