2020年高中数学新教材同步必修第一册 第3章 3．2.2 奇偶性 11页

3．2.2 奇偶性 第 1 课时 奇偶性的概念 学习目标 1.了解函数奇偶性的定义.2.掌握函数奇偶性的判断和证明方法.3.会应用奇、偶函 数图象的对称性解决简单问题． 知识点一 函数奇偶性的几何特征 一般地，图象关于 y 轴对称的函数称为偶函数，图象关于原点对称的函数称为奇函数． 知识点二 函数奇偶性的定义 1．偶函数：函数 f(x)的定义域为 I，如果∀x∈I，都有－x∈I，且 f(－x)＝f(x)，那么函数 f(x) 就叫做偶函数． 2．奇函数：函数 f(x)的定义域为 I，如果∀x∈I，都有－x∈I，且 f(－x)＝－f(x)，那么函数 f(x) 就叫做奇函数． 知识点三 奇(偶)函数的定义域特征 奇(偶)函数的定义域关于原点对称． 1．奇、偶函数的定义域都关于原点对称．( √ ) 2．函数 f(x)＝x2＋|x|的图象关于原点对称．( × ) 3．对于定义在 R 上的函数 f(x)，若 f(－1)＝f(1)，则函数 f(x)一定是偶函数．( × ) 4．不存在既是奇函数又是偶函数的函数．( × ) 一、函数奇偶性的判断 例 1 判断下列函数的奇偶性． (1)f(x)＝1 x ； (2)f(x)＝x2(x2＋2)； (3)f(x)＝ x x－1 ； (4)f(x)＝ x2－1＋ 1－x2. 解 (1)f(x)＝1 x 的定义域为(－∞，0)∪(0，＋∞)， ∵f(－x)＝ 1 －x ＝－1 x ＝－f(x)， ∴f(x)＝1 x 是奇函数． (2)f(x)＝x2(x2＋2)的定义域为 R. ∵f(－x)＝f(x)， ∴f(x)＝x2(x2＋2)是偶函数． (3)f(x)＝ x x－1 的定义域为(－∞，1)∪(1，＋∞)， ∵定义域不关于原点对称， ∴f(x)＝ x x－1 既不是奇函数，也不是偶函数． (4)f(x)＝ x2－1＋ 1－x2的定义域为{－1,1}． ∵f(－x)＝f(x)＝－f(x)＝0， ∴f(x)＝ x2－1＋ 1－x2既为奇函数，又为偶函数． 反思感悟 判断函数奇偶性的方法 (1)定义法： ①定义域关于原点对称； ②确定 f(－x)与 f(x)的关系． (2)图象法． 跟踪训练 1 判断下列函数的奇偶性． (1)f(x)＝ x； (2)f(x)＝ 1－x2 x ； (3)f(x)＝ x2＋x，x>0， x2－x，x<0. 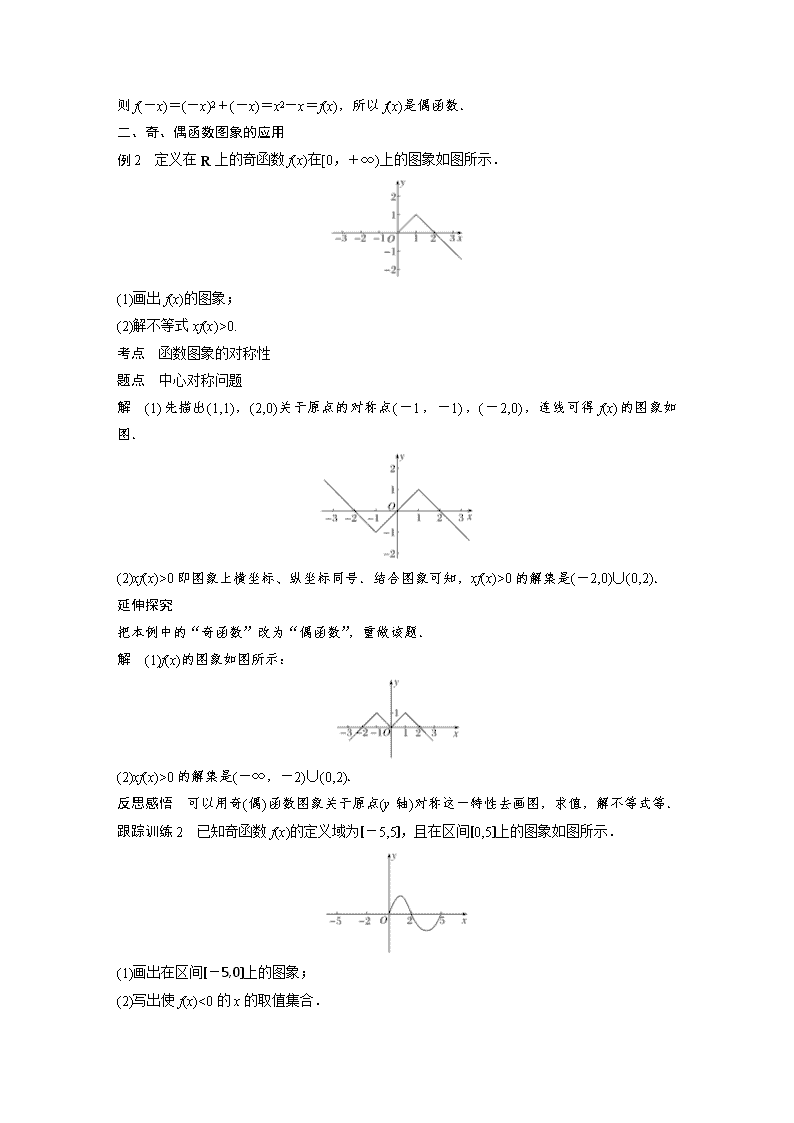解 (1)函数 f(x)的定义域为[0，＋∞)，不关于原点对称，所以 f(x)＝ x是非奇非偶函数． (2)f(x)的定义域为[－1,0)∪(0,1]，关于原点对称． f(－x)＝ 1－x2 －x ＝－f(x)， 所以 f(x)为奇函数． (3)f(x)的定义域为(－∞，0)∪(0，＋∞)，关于原点对称， 当 x>0 时，－x<0， 则 f(－x)＝(－x)2－(－x)＝x2＋x＝f(x)； 当 x<0 时，－x>0， 则 f(－x)＝(－x)2＋(－x)＝x2－x＝f(x)，所以 f(x)是偶函数． 二、奇、偶函数图象的应用 例 2 定义在 R 上的奇函数 f(x)在[0，＋∞)上的图象如图所示． (1)画出 f(x)的图象； (2)解不等式 xf(x)>0. 考点 函数图象的对称性 题点 中心对称问题 解 (1)先描出(1,1)，(2,0)关于原点的对称点(－1，－1)，(－2,0)，连线可得 f(x)的图象如图． (2)xf(x)>0 即图象上横坐标、纵坐标同号．结合图象可知，xf(x)>0 的解集是(－2,0)∪(0,2)． 延伸探究 把本例中的“奇函数”改为“偶函数”，重做该题． 解 (1)f(x)的图象如图所示： (2)xf(x)>0 的解集是(－∞，－2)∪(0,2)． 反思感悟 可以用奇(偶)函数图象关于原点(y 轴)对称这一特性去画图，求值，解不等式等． 跟踪训练 2 已知奇函数 f(x)的定义域为[－5,5]，且在区间[0,5]上的图象如图所示． (1)画出在区间[－5,0]上的图象； (2)写出使 f(x)<0 的 x 的取值集合． 考点 函数图象的对称性 题点 中心对称问题 解 (1)如图，在[0,5]上的图象上选取 5 个关键点 O，A，B，C，D. 分别描出它们关于原点的对称点 O′，A′，B′，C′，D′， 再用光滑曲线连接即得． (2)由(1)图可知，当且仅当 x∈(－2,0)∪(2,5)时，f(x)<0. ∴使 f(x)<0 的 x 的取值集合为{x|－2f(3)． 11．下列函数中，既是偶函数又在(0，＋∞)上单调递增的函数是( ) A．y＝x3 B．y＝|x|＋1 C．y＝－x2＋1 D．y＝－2 x 答案 B 解析 对于函数 y＝|x|＋1，f(－x)＝|－x|＋1＝|x|＋1＝f(x)， 所以 y＝|x|＋1 是偶函数，当 x>0 时，y＝x＋1， 所以在(0，＋∞)上单调递增． 另外，函数 y＝x3 不是偶函数，y＝－x2＋1 在(0，＋∞)上单调递减，y＝－2 x 不是偶函数．故 选 B. 12．设函数 f(x)和 g(x)分别是 R 上的偶函数和奇函数，则下列结论恒成立的是( ) A．f(x)＋|g(x)|是偶函数 B．f(x)－|g(x)|是奇函数 C．|f(x)|＋g(x)是偶函数 D．|f(x)|－g(x)是奇函数 考点 函数的奇偶性判定与证明 题点 判断抽象函数的奇偶性 答案 A 解析 由 f(x)是偶函数，可得 f(－x)＝f(x)， 由 g(x)是奇函数可得 g(－x)＝－g(x)， 故|g(x)|为偶函数， ∴f(x)＋|g(x)|为偶函数． 13．函数 f(x)＝ 4－x2 2－|x＋2| 的定义域为________，为______函数(填“奇”或“偶”)． 答案 [－2,0)∪(0,2] 奇 解析 依题意有 4－x2≥0， 2－|x＋2|≠0， 解得－2≤x≤2 且 x≠0， ∴f(x)的定义域为[－2,0)∪(0,2]． ∵f(x)＝ 4－x2 2－|x＋2| ＝ 4－x2 －x ＝－ 4－x2 x ，定义域关于原点对称， ∴f(－x)＝ 4－x2 x ＝－f(x)， ∴f(x)为奇函数． 14．函数 f(x)＝ax3＋bx＋c x ＋5 满足 f(－3)＝2，则 f(3)的值为________． 答案 8 解析 设 g(x)＝f(x)－5＝ax3＋bx＋c x(x≠0)， ∵g(－x)＝－ax3－bx－c x ＝－g(x)， ∴g(x)是奇函数， ∴g(3)＝－g(－3)＝－[f(－3)－5] ＝－f(－3)＋5＝－2＋5＝3， 又 g(3)＝f(3)－5＝3， ∴f(3)＝8. 15．已知函数 f(x)＝x2＋x＋1 x2＋1 ，若 f(a)＝2 3 ，则 f(－a)＝________. 考点 函数图象的对称性 题点 中心对称问题 答案 4 3 解析 根据题意，f(x)＝x2＋x＋1 x2＋1 ＝1＋ x x2＋1 ，而 h(x)＝ x x2＋1 是奇函数，故 f(－a)＝1＋h(－a) ＝1－h(a)＝2－[1＋h(a)]＝2－f(a)＝2－2 3 ＝4 3. 16．设函数 f(x)＝ax2＋1 bx＋c 是奇函数(a，b，c∈Z)，且 f(1)＝2，f(2)<3，求 a，b，c 的值． 解 由条件知 f(－x)＋f(x)＝0， ∴ax2＋1 bx＋c ＋ax2＋1 c－bx ＝0，∴c＝0. 又 f(1)＝2，∴a＋1＝2b. ∵f(2)<3，∴4a＋1 2b <3，∴4a＋1 a＋1 <3， 解得－1