2020年高中数学新教材同步必修第二册 第9章第 2 课时 总体取值规律的估计、总体百分位数的估计 13页

第 2 课时 总体取值规律的估计、总体百分位数的估计 学习目标 1.掌握从常见统计图表中获取有用的信息，体会统计数学在实际生活中的应用.2. 通过实例，理解百分位数的含义. 知识点一 常见统计图表的特点与区别 扇形图主要用于直观描述各类数据占总数的比例，条形图和直方图主要用于直观描述不同类 别或分组数据的频数和频率，条形图适用于描述离散型数据，直方图适用于描述连续型数据. 折线图主要用于描述数据随时间的变化趋势. 知识点二 百分位数 1.百分位数定义：一般地，一组数据的第 p 百分位数是这样一个值，它使得这组数据中至少 有 p%的数据小于或等于这个值，且至少有(100－p)%的数据大于或等于这个值. 2.常用的百分位数 (1)四分位数：第 25 百分位数，第 50 百分位数，第 75 百分位数. (2)其它常用的百分位数：第 1 百分位数，第 5 百分位数，第 95 百分位数，第 99 百分位数. 3.计算一组 n 个数据的第 p 百分位数的一般步骤如下： 第 1 步，按从小到大排列原始数据； 第 2 步，计算 i＝n×p%； 第 3 步，若 i 不是整数，而大于 i 的比邻整数为 j，则第 p 百分位数为第 j 项数据；若 i 是整 数，则第 p 百分位数为第 i 项与第(i＋1)项数据的平均数. 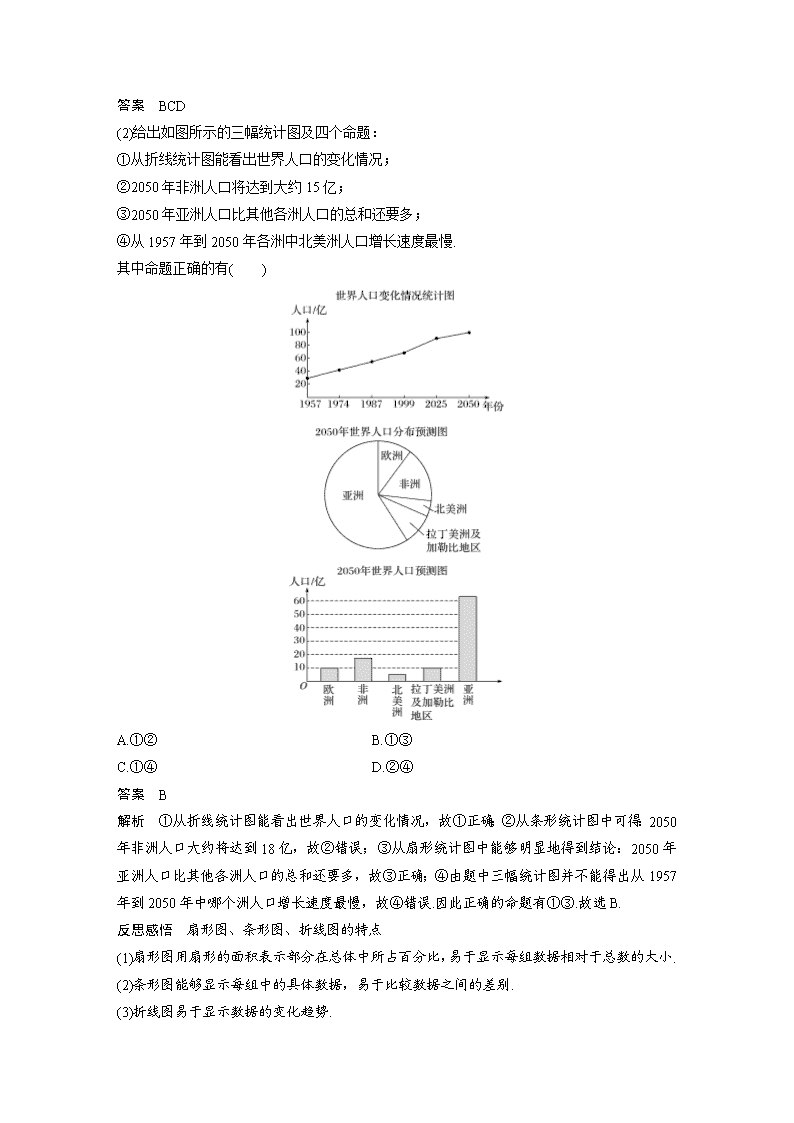1.为了更清楚地反映学生在这学期多次考试中数学成绩情况，可以选用折线统计图( √ ) 2.50%分位数就是中位数.( √ ) 3.100 个数据的 80%分位数是 85，那么这 100 个数据中一定有 80 个数小于或等于 85.( × ) 一、几种常见统计图表的特点 例 1 (1)(多选)下列说法中，正确的是( ) A.可以很清楚地表示出各部分同总体之间关系的统计图是条形统计图 B.能清楚地反映出数量增减变化的统计图是折线统计图 C.为了清楚地知道你的各科成绩，你可以选择制作条形统计图 D.为了清楚地反映出全校人数同各年级人数之间的关系，应选择扇形统计图 答案 BCD (2)给出如图所示的三幅统计图及四个命题： ①从折线统计图能看出世界人口的变化情况； ②2050 年非洲人口将达到大约 15 亿； ③2050 年亚洲人口比其他各洲人口的总和还要多； ④从 1957 年到 2050 年各洲中北美洲人口增长速度最慢. 其中命题正确的有( ) A.①② B.①③ C.①④ D.②④ 答案 B 解析 ①从折线统计图能看出世界人口的变化情况，故①正确；②从条形统计图中可得：2050 年非洲人口大约将达到 18 亿，故②错误；③从扇形统计图中能够明显地得到结论：2050 年 亚洲人口比其他各洲人口的总和还要多，故③正确；④由题中三幅统计图并不能得出从 1957 年到 2050 年中哪个洲人口增长速度最慢，故④错误.因此正确的命题有①③.故选 B. 反思感悟 扇形图、条形图、折线图的特点 (1)扇形图用扇形的面积表示部分在总体中所占百分比，易于显示每组数据相对于总数的大小. (2)条形图能够显示每组中的具体数据，易于比较数据之间的差别. (3)折线图易于显示数据的变化趋势. 跟踪训练 1 (1)根据下面给出的 2004 年至 2013 年我国二氧化硫排放量(单位：万吨)的柱形 图.以下结论不正确的是( ) A.逐年比较，2008 年减少二氧化硫排放量的效果最显著 B.2007 年我国治理二氧化硫排放显现成效 C.2006 年以来我国二氧化硫年排放量呈减少趋势 D.2006 年以来我国二氧化硫年排放量呈增加趋势 答案 D 解析 从 2006 年，将每年的二氧化硫排放量与前一年作差比较，得到 2008 年二氧化硫排放 量与 2007 年排放量的差最大，A 选项正确； 2007 年二氧化硫排放量较 2006 年降低了很多，B 选项正确； 虽然 2011 年二氧化硫排放量较 2010 年多一些，但自 2006 年以来，整体呈递减趋势，C 选项 正确，D 选项错误，故选 D. (2)下面的统计图反映了我国与“一带一路”沿线部分地区的贸易情况，2011～2016 年我国与 东南亚地区和东欧地区的贸易额统计图如图所示 (以上数据摘自《“一带一路”贸易合作大数据报告(2017)》). 根据统计图提供的信息，下列推断不合理的是( ) A.与 2015 年相比，2016 年我国与东欧地区的贸易额有所增长 B.2011～2016 年，我国与东南亚地区的贸易额逐年增长 C.2011～2016 年，我国与东南亚地区的贸易额的平均值超过 4 200 亿美元 D.2016 年我国与东南亚地区的贸易额比我国与东欧地区的贸易额的 3 倍还多 答案 B 二、几种常见的统计图表的应用 例 2 为了解某地区机动车拥有量对道路通行的影响，学校九年级社会实践小组对 2012 年～ 2019 年机动车拥有量、车辆经过人民路路口和学校门口的堵车次数进行调查统计，并绘制成 如图统计图： 根据统计图，回答下列问题： (1)写出 2018 年机动车的拥有量，分别计算 2012 年～2019 年在人民路路口和学校门口堵车次 数的平均数； (2)根据统计数据，结合生活实际，对机动车拥有量与人民路路口和学校门口堵车次数，说说 你的看法. 解 (1)2018 年机动车的拥有量为 3.4 万辆. 人民路路口的堵车次数平均数为 (54＋82＋86＋98＋124＋156＋196＋164)÷8＝120(次)， 学校门口的堵车次数平均数为 (65＋85＋121＋144＋128＋108＋77＋72)÷8＝100(次) (2)答案不唯一，如：2012 年～2015 年，随着机动车拥有量的增加，对道路的影响加大，年 堵车次数也增加；尽管 2019 年机动车拥有量比 2018 年增加，由于进行了交通综合治理，人 民路路口堵车次数反而降低明显. 反思感悟 利用统计图表解决实际生活中的问题，要认真观察、分析、研究统计图表，结合 统计图表的各自特点，充分利用统计思想、数形结合的思想解决问题. 跟踪训练 2 如图所示的是某粮店的大米、面粉、小米、玉米面的销售情况统计图，观察图 形，你能从中得到哪些信息？如果你是这家粮店的老板，你会怎么做？ 解 由扇形图可知 (1)面粉的销售量最大，需多进货； (2)小米的销售量最小，需少进货； (3)大米的销售量仅次于面粉的销售量，也应多进货. 三、百分位数 例 3 从某公司生产的产品中，任意抽取 12 件，得到它们的质量(单位：kg)如下： 7.9,9.0,8.9,8.6,8.4,8.5,8.5,8.5,9.9,7.8,8.3,8.0， 分别求出这组数据的 25%,75%,95%分位数. 解 将所有数据从小到大排列， 得 7.8,7.9,8.0,8.3,8.4,8.5,8.5,8.5,8.6,8.9,9.0,9.9， 因为共有 12 个数据， 所以 12×25%＝3,12×75%＝9,12×95%＝11.4， 则 25%分位数是8.0＋8.3 2 ＝8.15， 75%分位数是8.6＋8.9 2 ＝8.75， 95%分位数是第 12 个数据为 9.9. 反思感悟 计算一组 n 个数据的第 p 百分位数的一般步骤： 第 1 步：按照从小到大排列原始数据； 第 2 步：计算 i＝n×p%； 第 3 步：若 i 不是整数，大于 i 的比邻整数为 j，则第 p 百分位数为第 j 项数据，若 i 是整数， 则第 p 百分位数为第 i 项和第(i＋1)项数据的平均数. 跟 踪 训 练 3 某 歌 手 电 视 大 奖 赛 中 ， 七 位 评 委 对 某 选 手 打 出 如 下 分 数 ： 7.9,8.1,8.4,8.5,8.5,8.7,9.9，则其 50%分位数为________. 答案 8.5 解析 ∵7×50%＝3.5， ∴其 50%分位数是第 4 个数据为 8.5. 1.需要清楚地表示每个项目的具体数目应选择( ) A.折线统计图 B.扇形统计图 C.条形统计图 D.以上三者均可以 答案 C 2.下列关于 50%分位数的说法正确的是( ) A.50%分位数不是中位数 B.总体数据中的任意一个数小于它的可能性一定是 50% C.它是四分位数 D.它只适用于总体是离散型的数据 答案 C 解析 由百分位数的意义可知选项 A，B，D 错误. 3.二十四节气是中国劳动人民长期经验积累的结晶，它与白昼时长密切相关.当春分、秋分时， 昼夜时长大致相等；当夏至时，白昼时长最长.根据下图，在下列选项中白昼时长低于 11 小 时的节气是( ) A.惊蛰 B.小满 C.立秋 D.大寒 答案 D 解析 本题考查统计图，根据统计图易得大寒节气的白昼时长低于 11 小时，故选 D. 4.下列一组数据的 25%分位数是( ) 2.1,3.0,3.2,3.8,3.4,4.0,4.2,4.4,5.3,5.6 A.3.2 B.3.0 C.4.4 D.2.5 答案 A 解析 把该组数据按照由小到大排列，可得 2.1,3.0,3.2,3.4,3.8,4.0,4.2,4.4,5.3,5.6， 由 i＝10×25%＝2.5，不是整数， 则第 3 个数据 3.2 是 25%分位数. 5.某企业三个分厂生产同一种电子产品，三个分厂的产量分布如图所示.现在用分层随机抽样 方法从三个分厂生产的产品中共抽取 100 件进行使用寿命的测试，则第一分厂应抽取的件数 为________；测试结果为第一、二、三分厂取出的产品的平均使用寿命分别为 1 020 小时， 980 小时，1 030 小时，估计这个企业生产的产品的平均使用寿命为________小时. 答案 50 1 015 解析 由分层随机抽样可知， 第一分厂应抽取 100×50%＝50(件). 由样本的平均数估计总体的平均数，可知这批电子产品的平均使用寿命为 1 020×50%＋ 980×20%＋1 030×30%＝1 015(小时). 1.知识清单： (1)几种常见的统计图表. (2)百分位数. 2.方法归纳：数据分析、数形结合. 3.常见误区：求第 p 百分位数时，应先将数据从小到大排列. 1.如果想用统计图来反映各数据的变化趋势，比较合适的统计图是( ) A.条形图 B.折线图 C.扇形图 D.其他图形 答案 B 解析 能反映各数据的变化趋势的统计图是折线图. 2.已知 100 个数据的 75%分位数是 9.3，则下列说法正确的是( ) A.这 100 个数据中一定有 75 个数小于或等于 9.3 B.把这 100 个数据从小到大排列后，9.3 是第 75 个数据 C.把这 100 个数据从小到大排列后，9.3 是第 75 个数据和第 76 个数据的平均数 D.把这 100 个数据从小到大排列后，9.3 是第 75 个数据和第 74 个数据的平均数 答案 C 解析 因为 100×75%＝75 为整数， 所以第 75 个数据和第 76 个数据的平均数为 75%分位数，是 9.3. 3.(多选)如图所示，是根据某市 2015 年至 2019 年工业生产总值绘制的折线统计图，观察统计 图获得以下信息，其中信息判断正确的是( ) A.2015 年至 2019 年间工业生产总值逐年增加 B.2019 年的工业生产总值比前一年增加了 40 亿元 C.2017 年与 2018 年每一年与前一年比，其增长额相同 D.从 2016 年至 2019 年，每一年与前一年比，2019 年的增长率最大 答案 ABC 解析 由折线统计图可知：2015 年至 2019 年间工业生产总值逐年增加，所以 A 正确；2019 年的工业生产总值比前一年增加了 100－60＝40(亿元)，所以 B 正确；2017 年与 2018 年每一 年与前一年比，其增长额相同都是 20 亿元，所以 C 正确；从 2016 年至 2019 年，每一年与 前一年比，2017 年的增长率最大，为 100%，所以 D 错误. 4.数据 7.0,8.4,8.4,8.4,8.6,8.7,9.0,9.1 的 30%分位数为( ) A.8.4 B.8.5 C.8.6 D.8.3 答案 A 解析 因为 8×30%＝2.4，故 30%分位数是第三项数据 8.4. 5.某市教育局卫生健康所对全市高三年级的学生身高进行抽样调查，随机抽取了 100 名学生， 他们身高都处于 A，B，C，D，E 五个层次，根据抽样结果得到如下统计图表，则从图表中 不能得出的信息是( ) A.样本中男生人数少于女生人数 B.样本中 B 层次身高人数最多 C.样本中 D 层次身高的男生多于女生 D.样本中 E 层次身高的女生有 3 人 答案 C 解析 A.样本中男生人数为 4＋12＋10＋8＋6＝40，女生人数为 100－40＝60，所以样本中男 生人数少于女生人数，所以该选项是正确的； B.因为男生中 B 层次的比例最大，女生中 B 层次的比例最大，所以样本中 B 层次身高人数最 多，所以该选项是正确的； C.样本中 D 层次身高的男生有 8 人，女生 D 层次的有 60×15%＝9(人)，所以样本中 D 层次 身高的男生少于女生，所以该选项是错误的； D.样本中 E 层次身高的女生有 60×5%＝3(人)，所以该选项是正确的. 6.如图是某市连续 7 天的最高气温与最低气温的变化图，根据图中信息可知，这 7 天中最大 的日温差是________℃. 答案 11 7.已知 30 个数据的 60%分位数是 8.2，这 30 个数据从小到大排列后第 18 个数据是 7.8，则第 19 个数据是________. 答案 8.6 解析 由 30×60%＝18，设第 19 个数据为 x，则7.8＋x 2 ＝8.2，解得 x＝8.6，即第 19 个数据 是 8.6. 8.某校高二年级有 1 200 名学生，在体育考试前随机抽取部分学生进行体能测试，成绩分别记 为 A，B，C，D 共四个等级，其中 A 级和 B 级成绩为“优”，将测试结果绘制成如下条形统 计图和扇形统计图. 请根据图中信息，估计该校高二年级全体学生参加体能测试成绩为“优”的学生共有 ________人. 答案 870 解析 抽取的学生数为 60÷30%＝200， 所以 D 级学生占 15 200 ×100%＝7.5%， 所以成绩为“优”的学生共有 1 200×(1－20%－7.5%)＝870(人). 9.为使中华传统文化教育更具有实效性，某中学开展以“我最喜爱的传统文化种类”为主题 的调查活动，围绕“在诗词、国画、对联、书法、戏曲五种传统文化中，你最喜爱哪一种？(必 选且只选一种)”的问题，在全校范围内随机抽取部分学生进行问卷调查，将调查结果整理后 绘制成如图所示的不完整的统计图，请你根据图中提供的信息回答下列问题： (1)本次调查共抽取了多少名学生？ (2)通过计算补全条形统计图； (3)若该中学共有 960 名学生，请你估计该中学最喜欢国画的学生有多少名. 解 (1)24÷20%＝120(名)， ∴本次调查共抽取了 120 名学生. (2)120－24－40－16－8＝32(名)，∴最喜爱书法的学生有 32 名. 补全条形统计图，如图所示. (3)960× 40 120 ＝320(名). ∴估计该中学最喜欢国画的学生有 320 名. 10.某学校对男、女学生进行有关“习惯与礼貌”的评分，记录如下： 男：54,70,57,46,90,58,63,46,85,73,55,66,38,44,56,75,35,58,94,58 女：77,55,69,58,76,70,77,89,51,52,63,63,69,83,83,65,100,74 分别求男生、女生得分的四分位数. 解 对男生得分由小到大排序为 35,38,44,46,46,54,55,56,57,58,58,58,63,66,70,73,75,85,90,94，共 20 个数据， 所以 20×25%＝5,20×50%＝10,20×75%＝15， 则 25%分位数为46＋54 2 ＝50,50%分位数为58＋58 2 ＝58， 75%分位数为70＋73 2 ＝71.5. 对女生得分由小到大排序为 51,52,55,58,63,63,65,69,69,70,74,76,77,77,83,83,89,100，共 18 个数据. 所以 18×25%＝4.5,18×50%＝9,18×75%＝13.5， 则 25%分位数为 63,50%分位数为69＋70 2 ＝69.5， 75%分位数为 77. 11.春节期间，山东某著名旅游景点成为热门景点，大量游客慕名前往，省旅游局统计了春节 期间 5 天的游客数量，绘制了如图所示的折线统计图，则这五天游客数量的 50%分位数为 ( ) A.22.9 B.24.1 C.22.4 D.23.4 答案 D 解析 将这五天的游客数量(单位：万人)按从小到大的顺序排列为 21.8,22.4,23.4,24.8,25.4， 5×50%＝2.5，故 50%分位数为 23.4. 12.为了参加学校举行的传统文化知识竞赛，某班进行了四次模拟训练，将成绩优秀的人数和 优秀率绘制成如下两幅统计图： 在统计过程中造成统计图表数据模糊不清.但可以清楚的是第四次比第三次的优秀人数多 4 人，则第二次优秀人数为________人. 答案 28 解析 设该班共有 n 人，则 n×85%＝30＋4， n＝40， 第二次优秀人数为 40×70%＝28 人. 13.某省 30 年来，各项事业取得令人瞩目的成就，以 2016 年为例，全省社会固定资产总投资 约为 3 730 亿元，其中包括中央项目、省属项目、地(市)属项目、县(市)属项目和其他项目. 图 1，图 2 分别是这五个项目的投资额不完整的条形统计图和扇形统计图，请完成下列问题. (1)地(市)属项目投资额为________亿元； (2)在图 2 中，县(市)属项目部分所占百分比为 m%、对应的圆心角为β，则 m＝________，β ＝________度(m，β均取整数). 答案 (1)830 (2)18 65