河南省开封市2020届高三第三次模拟考试数学（文科）试题 Word版含解析 22页

- 1 - 2020 年河南省开封市高考数学三模试卷（文科） 一、选择题（共 12 小题）. 1. 已知集合  1,0,1,2,3A   ，  1 0B x x   ，则集合  RA C B （ ） A.  1,0 B.  1,0,1 C.  2,3 D.  1,2,3 【答案】B 【解析】 【分析】 根据已知求出 B 的补集，进而求交集． 【详解】解：由已知：  | 1RC B x x  ，所以集合    1,0,1RA C B   ． 故选：B． 【点睛】本题考查集合的补集和交集运算，属于基础题. 2. 设复数 1 2 1 iz i   ，则 z 的虚部为（ ） A. 1 2  B. ﹣1 C. 3 2 D. 1 2 i 【答案】A 【解析】 【分析】 根据复数的除法法则求出 z ，再写出 z 的虚部． 【详解】解：因为复数       1 2 11 2 3 3 1 1 1 1 2 2 2 i ii iz i i i          i， 则 z 的虚部为 1 2  ， 故选：A． 【点睛】本题主要考查复数的运算的复数的定义，属于基础题. 3. 已知 Sn 为等差数列 na 的前 n 项和，若 5 24S a ，则 7a ＝（ ） A. ﹣2 B. 0 C. 2 D. 10 【答案】B 【解析】 【分析】 - 2 - 设等差数列 na 的公差为 d，由已知结合等差数列的通项公式及求和公式得到 1 6 0,a d  即 得 7a 的值.． 【详解】解：设等差数列 na 的公差为 d，由 5 24S a ， 所以 1 1 15 10 4 4 , 6 0,a d a d a d      则 7 0a  ． 故选：B． 【点睛】本题主要考查等差数列的通项和求和公式，意在考查学生对这些知识的理解掌握水 平. 4. 设 a，b∈R，则“a＞b”是“a|a|＞b|b|”的（ ） A. 充分不必要条件 B. 必要不充分条件 C. 充要条件 D. 既不充分又不必要条件 【答案】C 【解析】 【分析】 根据不等式的基本性质，结合充分条件和必要条件的定义进行判断，即可得到结论． 【详解】由 a＞b， ①当 a＞b≥0 时，不等式 a|a|＞b|b|等价为a•a＞b•b，此时成立． ②当 0＞a＞b 时，不等式 a|a|＞b|b|等价为﹣a•a＞﹣b•b，即 a2＜b2，此时成立． ③当 a≥0＞b 时，不等式 a|a|＞b|b|等价为 a•a＞﹣b•b，即 a2＞﹣b2，此时成立， 即充分性成立； 由 a|a|＞b|b|， ①当 a＞0，b＞0 时，a|a|＞b|b|去掉绝对值得，（a﹣b）（a+b）＞0， 因为 a+b＞0，所以 a﹣b＞0，即 a＞b． ②当 a＞0，b＜0 时，a＞b． ③当 a＜0，b＜0 时，a|a|＞b|b|去掉绝对值得，（a﹣b）（a+b）＜0， 因为 a+b＜0，所以 a﹣b＞0，即 a＞b．即必要性成立， 综上可得“a＞b”是“a|a|＞b|b|”的充要条件， 故选：C． - 3 - 【点睛】本题主要考查了充要条件的判定，以及不等式的基本性质的综合应用，意在考查推 理与运算能力，属于中档试题. 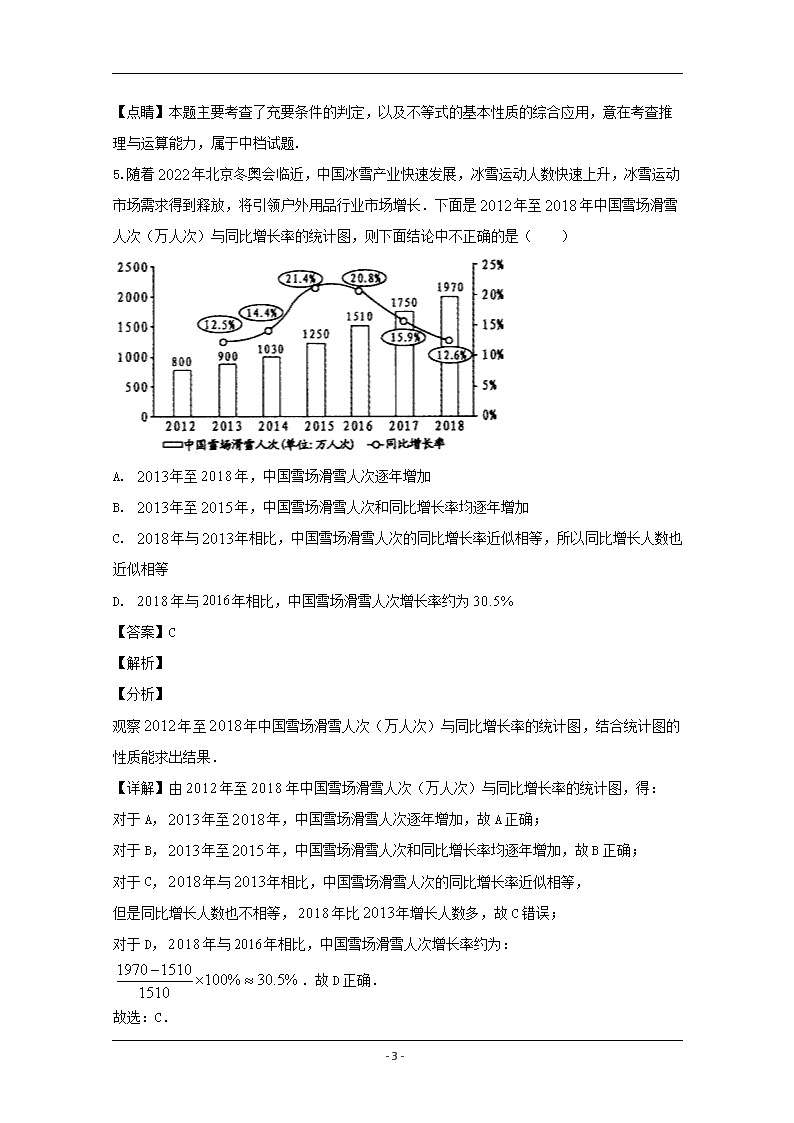5. 随着 2022 年北京冬奥会临近，中国冰雪产业快速发展，冰雪运动人数快速上升，冰雪运 动市场需求得到释放，将引领户外用品行业市场增长．下面是 2012 年至 2018 年中国雪场滑 雪人次（万人次）与同比增长率的统计图，则下面结论中不正确的是（ ） A. 2013年至 2018 年，中国雪场滑雪人次逐年增加 B. 2013年至 2015 年，中国雪场滑雪人次和同比增长率均逐年增加 C. 2018 年与 2013年相比，中国雪场滑雪人次的同比增长率近似相等，所以同比增长人数也 近似相等 D. 2018 年与 2016 年相比，中国雪场滑雪人次增长率约为30.5% 【答案】C 【解析】 【分析】 观察 2012 年至 2018 年中国雪场滑雪人次（万人次）与同比增长率的统计图，结合统计图的 性质能求出结果． 【详解】由 2012 年至 2018 年中国雪场滑雪人次（万人次）与同比增长率的统计图，得： 对于 A， 2013年至 2018 年，中国雪场滑雪人次逐年增加，故 A 正确； 对于 B， 2013年至 2015 年，中国雪场滑雪人次和同比增长率均逐年增加，故 B 正确； 对于 C， 2018 年与 2013年相比，中国雪场滑雪人次的同比增长率近似相等， 但是同比增长人数也不相等， 2018 年比 2013年增长人数多，故 C 错误； 对于 D， 2018 年与 2016 年相比，中国雪场滑雪人次增长率约为： 1970 1510 100% 30.5%1510    ．故 D 正确． 故选：C． - 4 - 【点睛】本题考查统计图表的应用，考查学生的数据分析能力，属于基础题. 6. 执行如图的程序框图，若输入 x 的值为 1 8 ，则输出的 y＝（ ） A. 1 4 B. 1 2 C. 2 D. 4 【答案】B 【解析】 【分析】 根据程序模拟运行,当满足条件时，计算 x 的值，并再次进入循环体，当不满足条件时退出循 环，计算并输出 y 的值，即可求解. 【详解】解：开始： 输入 1 8x = , 进入循环，满足条件 0x  ,计算 x 2 11 48log   ， 第二次进入循环，满足条件 0x  ,计算 x＝1﹣log24＝﹣1， 第三次进入循环，不满足条件 0x  , 退出循环，计算 1 12 2y   ． 输出 1 2 , 故选：B． - 5 - 【点睛】本题考查程序框图的输入输出值的确定，涉及循环结构，对数运算，属基础题，难 度较易. 7. 正方体 1 1 1 1ABCD A B C D 中， 1AB 与平面 1 1ABC D 所成的角为（ ） A. 30° B. 45 C. 60 D. 90 【答案】A 【解析】 【分析】 连接 1CB 交 1BC 于点 E，连接 AE，求角 1B AE 即可． 【详解】如图，连接 1CB 交 1BC 于点 E，连接 AE， 正方体中，证得： 1CB  平面 1 1ABC D ， 所以 1AB 与平面 1 1ABC D 所成的角为 1B AE ， 设正方体的边长为 a ， 在 1B AE 中，求得： 1 2AB a ， 1 2 2 aB E  ， 1 1 1 1sin 2 B EB AE AB    ,所以 1 30B AE   ， 故选 A 【点睛】本题主要考查了线面角知识，关键是作出对应的一个平面角，解三角形即可，属于 基础题． 8. “二进制”来源于我国古代的《易经》，该书中有两类最基本的符号：“─”和“﹣﹣”， 其中“─”在二进制中记作“1”，“﹣﹣”在二进制中记作“0”．如符号“☱”对应的二 进制数 011（2）化为十进制的计算如下：011（2）＝0×22+1×21+1×20＝3（10）．若从两类符号中任 取 2 个符号进行排列，则得到的二进制数所对应的十进制数大于 2 的概率为（ ） - 6 - A. 1 2 B. 1 3 C. 2 3 D. 1 4 【答案】D 【解析】 【分析】 分类计算得到从两类符合中任取 2 个符号排列，则组成不同的十进制数为 0，1，2，3，即可 计算得到概率． 【详解】根据题意，不同符号可分为三类： 第一类：由两个“─”组成，其二进制为：11（2）＝3（10）； 第二类：由两个“﹣﹣“组成，其二进制为：00（2）＝0（10）； 第三类：由一个“─”和一个“﹣﹣”组成，其二进制为：10（2）＝2（10），01（2）＝1（10）， 所以从两类符号中任取 2 个符号排列，则组成不同的十进制数为 0，1，2，3， 则得到的二进制数所对应的十进制数大于 2 的概率 P 1 4  ． 故选：D． 【点睛】本题主要考查了古典概型及其概率的计算，以及转化的应用，意在考查学生的计算 能力和应用能力，属于中档试题. 9. 已知函数 f（x）＝x（x﹣c）2 在 x＝2 处有极大值，则 c＝（ ） A. 2 或 2 3 B. 6 C. 2 D. 2 或 6 【答案】B 【解析】 【分析】 由函数 f（x）＝x（x﹣c）2 在 x＝2 处有极大值，则必有 f′（2）＝0，且在 x＝2 的左侧附近 f′（x）＞0，右侧附近 f′（x）＜0，据此即可求出 c 的值． 【详解】因为 f′（x）＝（x﹣c）2+2x（x﹣c）＝3x2﹣4cx+c2， 且函数 f（x）＝x（x﹣c）2 在 x＝2 处有极大值， 所以 f′（2）＝0，即 c2﹣8c+12＝0，解得 c＝6 或 2． 经检验 c＝2 时，函数 f（x）在 x＝2 处取得极小值，不符合题意，应舍去． 故 c＝6， 故选：B． 【点睛】本题主要考查了利用导数研究函数的极值问题，其中解答中熟练应用导数研究函数 - 7 - 的极值的方法是解答的关键，意在考查推理与运算能力. 10. 已知 A 是△ABC 的一个内角，且 sinA+cosA＝a，其中 a∈（0，1），则关于 tanA 的值，以 下答案中，可能正确的是（ ） A. ﹣2 B. 1 2  C. 1 2 D. 2 【答案】A 【解析】 【分析】 把已知的等式两边平方，由同角三角函数间的基本关系化简后，得到 2sinAcosA＝a2﹣1＜0， 进而得到 cosA＜0，得到 sinA＞﹣cosA，再结合三角函数的基本关系式，求得 tanA 值的范围， 即可判断出符合题意的 tanA 值的可能值． 【详解】由 sinA+cosA＝a，两边平方得：（sinA+cosA）2＝a2， 即 sin2A+cos2A+2sinAcosA＝1+2sinAcosA＝a2， 又因为 a∈（0，1），所以 2sinAcosA＝a2﹣1＜0， 因为 0＜A＜π，得到sin 0A  ，所以 cosA＜0， 又由 sinA+cosA＝a＞0，所以 sinA＞﹣cosA＞0， 则 tanA＜﹣1．比较四个选项，只有 A 正确． 故选：A． 【点睛】本题主要考查了三角函数基本关系式的综合应用，意在考查推理与运算能力，属于 中档试题. 11. 在棱长为 1 的正方体 ABCD﹣A1B1C1D1 中，点 E，F 分别是棱 C1D1，B1C1 的中点，P 是上底面 A1B1C1D1 内一点，若 AP∥平面 BDEF，则线段 AP 长度的取值范围是（ ） A. [ 5 2 ， 2 ] B. [ 3 2 4 ， 5 2 ] C. [ 3 2 8 ， 6 2 ] D. [ 6 2 ， 2 ] 【答案】B 【解析】 【分析】 分别取棱 A1B1、A1D1 的中点 M、N，连接 MN，可证平面 AMN∥平面 BDEF，得 P 点在线段 MN 上．由 此可判断当 P 在 MN 的中点时，AP 最小；当 P 与 M 或 N 重合时，AP 最大．然后求解直角三角 - 8 - 形得答案． 【详解】如图所示，分别取棱 A1B1、A1D1 的中点 M、N，连接 MN，连接 B1D1， ∵M、N、E、F 为所在棱的中点，∴MN∥B1D1，EF∥B1D1， ∴MN∥EF，又 MN⊄ 平面 BDEF，EF⊂平面 BDEF，∴MN∥平面 BDEF； 连接 NF，由 NF∥A1B1，NF＝A1B1，A1B1∥AB，A1B1＝AB， 可得 NF∥AB，NF＝AB，则四边形 ANFB 为平行四边形， 则 AN∥FB，而 AN⊄ 平面 BDEF，FB⊂平面 BDEF，则 AN∥平面 BDEF． 又 AN∩NM＝N，∴平面 AMN∥平面 BDEF． 又 P 是上底面 A1B1C1D1 内一点，且 AP∥平面 BDEF，∴P 点在线段 MN 上． 在Rt△AA1M 中，AM 2 2 1 1 1 51 4 2AA A M     ， 同理，在 Rt△AA1N 中，求得 AN 5 2  ，则△AMN 为等腰三角形． 当 P 在 MN 的中点时，AP 最小为 2 22 3 21 ( )4 4   ， 当 P 与 M 或 N 重合时，AP 最大为 2 21 51 ( )2 2   ． ∴线段 AP 长度的取值范围是[ 3 2 4 ， 5 2 ]． 故选：B． 【点睛】本题主要考查了空间中点、线、面间的距离问题，其中解答中通过构造平行平面寻 找得到点 P 的位置是解答的关键，意在考查空间想象能力与运算能力，属于中档试题. - 9 - 12. 若函数  f x 对 a 、b R ，同时满足：（1）当 0a b  时有     0f a f b  ；（2） 当 0a b  时有     0f a f b  ，则称  f x 为  函数．下列函数中：①   sinx x xf  ； ②   x xf x e e  ；③   x xf x e e  ；④   0, 0 1 , 0 x f x xx    .是  函数的为（ ） A. ①② B. ②③ C. ③④ D. ①④ 【答案】A 【解析】 【分析】 由题意可得  y f x 满足是 R 上的奇函数，且为增函数，称为  函数，由函数的奇偶性和单 调性与导数之间的关系，分别判断①、②、③、④的函数的奇偶性和单调性，可得所求结论． 【详解】由（1）当 0a b  时有     0f a f b  ，即为    f a f a   ，则  y f x 为 R 上的奇函数； 由（2）当 0a b  时有     0f a f b  ，即为 a b  ，      f a f b f b    ， 可得  y f x 为 R 上的增函数， 则函数  y f x 为 R 上的奇函数，且为增函数． 由①   sinx x xf  ，定义域为 R ，        sin sin sinf x x x x x x x f x             ,即  y f x 为奇函数， 又   1 cos 0f x x    ，可得  y f x 为 R 上的增函数，故①是  函数； ②   x xf x e e  ，定义域为 R ，      x x x xf x e e e e f x         ，即  y f x 为 奇函数， 又   0x xf x e e  ，可得  y f x 为 R 上的增函数，故②是  函数； ③   x xf x e e  ，定义域为 R ，    x xf x e e f x    ，可得  y f x 为偶函数，故 ③不是  函数； - 10 - ④   0, 0 1 , 0 x f x xx    ，定义域为 R ， 0x  时，    1 1f x f xx x       ，可得  y f x 为奇函数， 又  y f x 在  ,0 ， 0,  上单调递增，但在 R 上不为增函数，比如    1 1f f  ， 故④不是  函数． 故选：A． 【点睛】本题考查函数的新定义，主要考查函数的奇偶性与单调性的判断，考查推理能力， 属于中等题. 二、填空题：本题共 4 小题，每小题 5 分，共 20 分． 13. 已知 x，y 满足约束条件 2, 1, 2 2 0, x y x y      „ „ … 则 z x y  的最大值为________. 【答案】4 【解析】 【分析】 作出可行域，作目标函数对应的直线，平移该直线可得最优解． 【详解】作出可行域，如图 ABC 内部（含边界），作直线 0x y  ，向下平行直线l ，z x y  增大，当 l 过点 (2, 2)A  时， 2 ( 2) 4z     为最大值． 故答案为：4． - 11 - 【点睛】本题考查简单的线性规划，作出可行域是解题关键． 14. 设向量  1,2a  ，  1,0b  ，若  a ma b    ，则实数 m  _____． 【答案】 1 5 【解析】 【分析】 根据题意，先求出 ma b  的坐标，由向量垂直与向量数量积的关系可得   0a ma b    ，求 解即可． 【详解】解：根据题意，  1,2a  ，  1,0b  ，则  1,2ma b m m   . 若  a ma b    ，则   1 4 0a ma b m m       ，解得 1 5m  . 故答案为： 1 5 ． 【点睛】本题考查向量垂直、向量数量积坐标运算，属于基础题. 15. 已知正项数列 na 的前 n 项和为 nS ，且对于任意 *,p q N ，有 p q p qa a a  ，若 a2=4， 则 1a  _____， 6S  _____． 【答案】 (1). 2 (2). 126 【解析】 【分析】 根据已知条件，对 p，q 的依次取特值，求出数列的前 6 项，即可得到结果． 【详解】解：正项数列 na 的前 n 项和为 nS ，且对于任意 *,p q N ，有 p q p qa a a  ， ∵ 2a 4 ， 当 1p q  时， 1 1 2 4a a a  ，所以 1 2a  ， 当 1 2p q ， 时， 1 2 3a a a ，所以 3 8a  ， 当 2 2p q ， 时， 2 2 4a a a ，所以 4 16a  ， 当 3 2p q ， 时， 3 2 5a a a ，所以 5 32a  ， 当 3 3p q ， 时， 3 3 6a a a ，所以 6 64a  ， - 12 - 所以 6 2 4 8 16 32 64 126S        ； 故答案为：2；126． 【点睛】本题考查数列的递推关系，数列的求和，属基础题，难度较易. 16. 已知 1F 、 2F 是椭圆 2 2 2 2: 1( 0)x yC a ba b     的左，右焦点，点 P 为C 上一点，O 为坐 标原点， 2POFV 为正三角形，则C 的离心率为__________． 【答案】 3 1 【解析】 【分析】 结合等边三角形的性质和椭圆的定义列方程，化简后求得椭圆的离心率. 【详解】如图,因为 2POFV 为正三角形，所以 1 2| | | | | |OF OP OF  ， 所以 1 2F PF 是直角三角形. 因为 2 1 60PF F   ， 2 1| | 2F F c ，所以 2| |PF c , 1| | 3PF c . 因为 2 1| | | | 2PF PF a  ，所以 3 2c c a  即 2 3 1 3 1 c a = = - + ，所以 3 1e   . 故答案为： 3 1 【点睛】本小题主要考查椭圆离心率的求法，考查椭圆的定义，属于基础题. 三、解答题：共 70 分．解答应写出文字说明，证明过程或演算步骤．第 17～21 题为必考题， 每个试题考生都必须作答．第 22、23 题为选考题，考生根据要求作答．（一）必考题：共 60 分． - 13 - 17. 在△ABC 中，D 为边 AC 上的点，BD＝3，且 3 BD•cos∠BDC＝BC•sin∠C． （1）求∠BDC； （2）若△ABD 的面积为 3 3 4 ，求 AB． 【答案】（1） 3  ；（2）AB 13 . 【解析】 【分析】 （1）结合正弦定理即可求解； （2）先根据面积求得 AD，进而结合余弦定理即可求解． 【详解】（1）因为 3 BD•cos∠BDC＝BC•sin∠C， 由正弦定理得 3 sin∠C•cos∠BDC＝sin∠BDC•sin∠C． 因为 sin∠C≠0 可得 tan∠BDC 3 ⇒∠BDC 3  ； （2）∴△ABD 的面积为 3 3 4 ， ∴ 1 2 BD×AD×sin（π﹣∠BDC） 3 3 4  ⇒ 3 2 AD•sin 2 3 3 3 4   ⇒AD＝1； ∴AB2＝AD2+BD2﹣2AD•BDcos（π﹣∠BDC）＝32+12﹣2 13 1 2         13； ∴AB 13 ． 【点睛】本题考查利用正弦定理和余弦定理解三角形，属综合基础题. 18. 如图，四棱锥 P﹣ABCD 中，四边形 ABCD 是边长为 2 的正方形，△PAD 为等边三角形，E， F 分别为 PC 和 BD 的中点，且 EF⊥CD． （1）证明：平面 PAD⊥平面 ABCD； （2）求点 C 到平面 PDB 的距离． - 14 - 【答案】（1）证明见解析；（2） 2 21 7 . 【解析】 【分析】 （1）根据中位线定理可证 PA⊥CD，结合 AD⊥CD 可得 CD⊥平面 PAD，于是平面 PAD⊥平面 ABCD； （2）计算△PBD 的面积，根据 VP﹣BCD＝VC﹣PBD 列方程计算点 C 到平面 PDB 的距离． 【详解】（1）因为 E，F 分别为 PC 和 BD 的中点，所以 EF∥PA， 又因为 EF⊥CD，所以 PA⊥CD， 因为四边形 ABCD 是正方形，所以 AD⊥CD， 又 PA∩AD＝A，PA⊂平面 PAD，AD⊂平面 PAD，所以 CD⊥平面 PAD， 又 CD⊂平面 ABCD，所以平面 PAD⊥平面 ABCD． （2）取 AD 的中点 O，连接 PO， 因为△PAD 是等边三角形，AD＝2，所以 PO⊥AD，且 PO 3 ， 又平面 PAD⊥平面 ABCD，平面 PAD∩平面 ABCD＝AD， 所以 PO⊥平面 ABCD， 又四边形 ABCD 是边长为 2 的正方形，所以 S△BCD 1 2 22     2， 所以 VP﹣BCD 1 2 32 33 3     ， 连接 OB，则 OB 2 2 5AO AB   ，故 PB 2 2PO OB   2 2 ， 又 BD 2 2AB AD   2 2 ，PD＝2， 所以 S△PBD 2 21 2 (2 2) 1 72      ， 设 C 到平面 PBD 的距离为 h，则 VC﹣PBD 1 773 3 hh    ， 整理得 7 2 3 3 3 h  ，解得 h 2 21 7  ， 即点 C 到平面 PBD 的距离为 2 21 7 ． - 15 - 【点睛】本题主要考查了平面与平面垂直的判定与证明，以及点到平面的距离的求解，其中 解答中熟记线面位置关系的判定定理和性质定理，以及合理利用“等体积法”求解点到平面 的距离是解答的关键，着重考查了推理与运算能力. 19. 已知抛物线 C：x2＝2py（p＞0），F 为抛物线 C 的焦点．以 F 为圆心，p 为半径作圆，与 抛物线 C 在第一象限交点的横坐标为 2． （1）求抛物线 C 的方程； （2）直线 y＝kx+1 与抛物线 C 交于 A，B 两点，过 A，B 分别作抛物线 C 的切线 l1，l2，设切 线 l1，l2 的交点为 P，求证：△PAB 为直角三角形． 【答案】（1） 2 4x y ；（2）证明见解析. 【解析】 【分析】 （1）由题意可得 M 点的坐标为 (2, )2 p ，代入抛物线方程，即可求出 p 的值； （2）设 2 2 1 2 1 2( , ), ( , )4 4 x xA x B x ，利用导数的几何意义得到 A，B 两点处的切线斜率分别为 1 1 1 2k x ， 2 2 1 2k x ，联立直线与抛物线方程，利用韦达定理得到 k1k2＝﹣1，从而得到△PAB 为直角三角形． 【详解】（1）记抛物线 C 与圆 F 在第一象限的交点为 M， 由圆 F 与抛物线 C 的准线相切，且 M 到抛物线 C 准线的距离等于圆 F 的半径 p ， 所以 M 点的坐标为 (2, )2 p ，代入抛物线方程得： 2 4( 0)p p  ， 所以 2p  ，所以抛物线的方程为 2 4x y . （2）设 2 2 1 2 1 2( , ), ( , )4 4 x xA x B x ， 由 2 4x y ，可得 y 21 4 x ，则 1 2y x  ， - 16 - 所以 A，B 两点处的切线斜率分别为 1 1 1 2k x ， 2 2 1 2k x ， 由 2 1 4 y kx x y     ，得 2 4 4 0x kx   ，所以 1 2 1 24 , 4x x k x x    ， 所以 1 2 1 2 1 14k k x x   ， 所以 PA PB ，即 PAB 为直角三角形． 【点睛】本题主要考查抛物线的标准方程的求解、及直线与抛物线的位置关系的综合应用,解 答此类题目，通常联立直线方程与抛物线方程，应用一元二次方程根与系数的关系进行求解， 此类问题易错点是复杂式子的变形能力不足，导致错解，能较好的考查考生的逻辑思维能力、 运算求解能力、分析问题解决问题的能力等． 20. 某公司为确定下一年度投入某种产品的宣传费，需了解年宣传费 x（单位：千元）对年销 售量 y（单位：t）和年利润 z（单位：千元）的影响，对近 8 年的年宣传费 ix 和年销售量 iy （ 1,2 8 i ）数据作了初步处理，得到下面的散点图及一些统计量的值． x y w   8 2 1 i i x x     8 2 1 i i w w      8 1 i i i x x y y       8 1 i i i w w y y    46.6 563 6.8 289.8 1.6 1.469 108.8 表中  iiw x ， 8 1 1 8  i iw w （1）根据散点图判断， y a bx  与 y c d x  哪一个适宜作为年销售量 y 关于年宣传费 x 的回归方程类型？ 给出判断即可，不必说明理由 - 17 - （2）根据（1）的判断结果及表中数据，建立 y 关于 x 的回归方程； （3）已知这种产品的年利润 z 与 x、y 的关系为 0.2z y x  根据（2）的结果回答下列问题： ①年宣传费 49x  时，年销售量及年利润的预报值是多少？ ②年宣传费 x 为何值时，年利润的预报值最大？ 附：对于一组数据     1 1 2 2, , , , , ,n nu v u v u v ，其回归线 v u   的斜率和截距的最小二 乘估计分别为：      1 2 1 ˆ        n i i i n i i u u v v u u ， ˆˆ v u   ． 【答案】（1）y c d x  适宜；（2） ˆ 100.6 68y x  ；（3）①576.6，,6.32；② 46.24x  【解析】 【分析】 （1）由图中散点的大致形状，可以判断 y c d x  适宜作为年销售量 y 关于年宣传费 x 的 回归方程类型； （2）令 w x ，先建立 y 关于 w 的线性回归方程，进而可得到 y 关于 x 的回归方程. （3）①由（2），可求出 49x  时，年销售量 y 的预报值，再结合年利润 0.2z y x  ，计算 即可； ②根据（2）的结果，可求得年利润 z 的预报值 ˆ 13.6 20.12z x x    ，求出最值即可. 【详解】（1）由图中散点的大致形状，可以判断 y c d x  适宜作为年销售量 y 关于年宣传 费 x 的回归方程类型. （2）令 w x ，先建立 y 关于 w 的线性回归方程， 由于      8 1 8 2 1 108.8ˆ 681.6 i i i i i w w y y d w w           ， ˆˆ 563 68 6.8 100.6c y dw      ， 所以 y 关于 w 的线性回归方程为 ˆ 100.6 68y w  ， 因此 y 关于 x 的回归方程为 ˆ 100.6 68y x  . （3）①由（2）知，当 49x  时，年销售量 y 的预报值 ˆ 100.6 68 49 576.6  y ， - 18 - 年利润 z 的预报值 ˆ 576.6 0.2 49 66.32z     . ②根据（2）的结果可知，年利润 z 的预报值 ˆ 0.2(100.6 68 ) 13.6 20.12z x x x x       ， 当 13.6 6.82x   时，即当 46.24x  时， ˆz 取得最大值. 故年宣传费为 46.24 千元时，年利润的预报值最大． 【点睛】本题考查回归方程及其应用，考查利用二次函数求最值，考查学生的计算求解能力， 属于中档题. 21. 已知函数    ln af x x a Rx    的图象在点 1 1, fe e         处的切线斜率为 e ，其中 e 为 自然对数的底数． （1）求实数 a 的值，并求  f x 的单调区间； （2）证明：   x xxf x e  ． 【答案】（1） 2a e  ，函数的单调递减区间 20, e      ，函数单调递增区间 2 e      ， ；（2）证明 见解析. 【解析】 【分析】 （1）先对函数求导，然后结合导数的几何意义可求 a ，结合导数与单调性关系即可求解． （2）要证明原不等式成立，可转化为证明求解相应函数的范围，进行合理的变形后构造函数， 结合导数可证． 【详解】解：（1）函数  f x 的定义域为( )0,+¥ .   2 1' af x x x   ，由题意可得， 21'f e aee         e，故 a 2 e  ，   2 2 1 2 2' exf x x ex ex    . 当 20,x e     时， ( ) 0f x¢ < ，函数  f x 单调递减，当 2 ,x e      时， ( ) 0f x¢ > ，函数  f x 单调递增，故函数  f x 的单调递减区间为 20, e      ，单调递增区间为 2 ,e     . - 19 - （2）证明：设     2lnh x xf x x x e    ，则    ln 1 0h x x x   . 当 x 10 e     ， 时，   0h x  ，函数  h x 单调递减，当 x 1 e       ， 时，   0h x  ，函数  h x 单调递增，故  min 1 1h x h e e      . 设   x xt x e  ，则   1' x xt x e  ，当  0,1x 时，   0t x  ，函数  t x 单调递增，当  1, x 时，   0t x  ，函数  t x 单调递减，故    max 11t x t e   . 综上可得， 0x  时，恒有    h x t x ，即   x xxf x e  ． 【点睛】本题考查函数的单调区间、不等式恒成立的证明问题，属于中档题. （二）选考题：共 10 分．请考生在第 22、23 题中任选一题作答．如果多选，则按所做的第 一题计分．[选修 4-4：坐标系与参数方程] 22. 在平面直角坐标系 xOy 中，曲线 C1 的参数方程为 1 x cos y sin       （φ为参数）．以坐标原点 O 为极点，x 轴的正半轴为极轴建立极坐标系，曲线 C2 的极坐标方程为 2 3 cos  ，曲线 C1 和 C2 在第一象限交于点 A． （1）求点 A 的直角坐标； （2）直线 ( (0, ), )3       R 与曲线 C1，C2 在第一象限分别交于点 B，C，若△ABC 的面 积为 3 ，求α的值． 【答案】（1）（ 3 3 2 2 ， ）；（2） 12   . 【解析】 【分析】 （1）直接利用转换关系，把参数方程、极坐标方程和直角坐标方程之间进行转换． （2）利用三角形面积公式和三角函数关系式，求出结果． 【详解】（1）曲线 C1 的参数方程为 1 x cos y sin       （ 为参数）， - 20 - 转换为直角坐标方程为 22 ( 1) 1yx    .根据 2 2 2 x cos y sin x y            22 ( 1) 1yx    转换为极坐标方程为 2sin  . 联立曲线 C1 和 C2 得到： 2 3 2sin cos       ，解得 3 3      ， 即 ( 3 )3 ，A 转换为直角坐标为（ 3 3 2 2 ， ）． （2）连接 OA，由（1）得： ( 3 )3 ，A ， 可得：|OA| 3 ， 3AOx   ， 将直线  与曲线 C1 和 C2 联立可得： (2sin )， B ， (2 3 )， C cos . 2sin OB ， 2 3OC cos ，    COx BOx ，所以 3AOB AOC       ． 则：S△ABC＝S△AOC﹣S△AOB 1 1 2 2OA OC sin AOC OA OB sin AOB       ， 1 13 2 3 3 22 3 2 3sin sin sin sin                       ，  3 33sin cos sin         ， 22 3 33sin        ， 整理得 2 1 3 2sin       ， 所以 12   ． 【点睛】本题考查了参数方程、极坐标方程和直角坐标方程之间的转换、三角形面积公式、 三角函数关系式，考查了数学运算能力，逻辑推理能力，转化数学思维，属于中档题. [选修 4-5：不等式选讲] - 21 - 23. 关于 x 的不等式  *| 2 |x m m N   的解集为 A，且 3 2 ∈A， 1 2 ∉ A． （1）求 m 的值； （2）设 a，b，c 为正实数，且 3a b c m   ，求  a b c 的最大值． 【答案】（1） 1m  ；（2）3． 【解析】 【分析】 （1）根据集合的特点可得 3 2 ∈A， 1 2 ∉ A，从而得到关于 m 的不等式，即可得答案； （2）利用基本不等式，即可得答案； 【详解】（1）∵ 3 2 ∈A， 1 2 ∉ A， 3 12 , 22 2m m     ，∴ 1 3 2 2m  *, 1m N m   . （2）a，b，c 为正实数，且 3a b c   ， ∴ 1 1 1a b c a b c        1 1 1 ( ) 3 3 3 32 2 2 2 2 a b c a b c            ． 当且仅当 1a b c   时取等号． ∴  a b c 的最大值为 3． 【点睛】本题考查利用不等式的解集确定参数值，以及利用基本不等式求最值，属综合基础 题. - 22 -