高中数学分章节训练试题：36点、直线、平面之间的位置关系 5页

高三数学章节训练题36《点、直线、平面之间的位置关系》‎ 时量：60分钟 满分：80分 班级： 姓名： 计分：‎ ‎ 个人目标：□优秀（‎70’‎~‎80’‎） □良好（‎60’‎～‎69’‎） □合格（‎50’‎～‎59’‎）‎ 一、选择题(本大题共6小题，每小题5分，满分30分)‎ ‎1．已知各顶点都在一个球面上的正四棱柱（其底面是正方形，且侧棱垂直于底面）高为，体积为，则这个球的表面积是（ ）‎ ‎ Ａ．　　　　Ｂ．　　　　Ｃ．　　　　Ｄ．‎ ‎2．已知在四面体中，分别是的中点，若，则与所成的 角的度数为（　　）‎ Ａ．　　　Ｂ．　　　‎ Ｃ．　　 Ｄ．‎ ‎3．三个平面把空间分成部分时，它们的交线有（　　）‎ Ａ．条　　Ｂ．条　　‎ Ｃ．条　　Ｄ．条或条 ‎4．在长方体，底面是边长为的正方形，高为，则点到截面的距离为( ) ‎ A． B． C． D． ‎ ‎5．直三棱柱中，各侧棱和底面的边长均为，点是上任意一点，连接，则三棱锥的体积为（ ）‎ A． B． C． D．‎ ‎6．下列说法不正确的是（ ）‎ A．空间中，一组对边平行且相等的四边形是一定是平行四边形；‎ B．同一平面的两条垂线一定共面；‎ C．过直线上一点可以作无数条直线与这条直线垂直，且这些直线都在同一个平面内；‎ D．过一条直线有且只有一个平面与已知平面垂直.‎ 二、填空题(本大题共5小题，每小题5分，满分25分)‎ ‎1．正方体各面所在的平面将空间分成_____________部分。翰林汇 ‎2．空间四边形中，分别是的中点，则与的位置关系是_____________；四边形是__________形；当___________时，四边形是菱形；当___________时，四边形是矩形；当___________时，四边形是正方形 ‎3．四棱锥中，底面是边长为的正方形，其他四个侧面都是侧棱长为的等腰三角形，则二面角的平面角为_____________。翰林汇 ‎4．三棱锥则二面角的大小为____翰林汇 ‎5．为边长为的正三角形所在平面外一点且，则到的距离为______。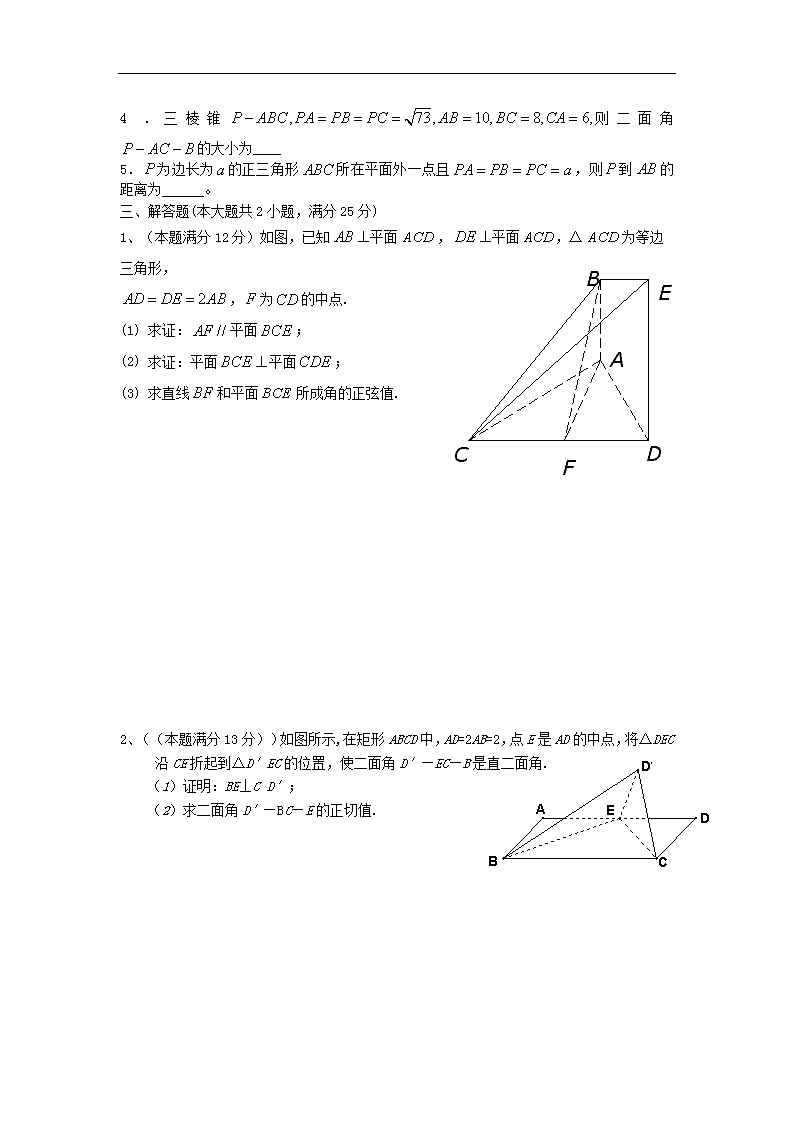翰林汇 三、解答题(本大题共2小题，满分25分) ‎ A B C D E F ‎1、（本题满分12分）如图，已知平面，平面，△为等边三角形，‎ ‎，为的中点.‎ ‎(1) 求证：平面；‎ ‎(2) 求证：平面平面；‎ ‎(3) 求直线和平面所成角的正弦值.‎ ‎ ‎ ‎2、（（本题满分13分））如图所示,在矩形ABCD中，AD=2AB=2，点E是AD的中点，将△DEC沿CE折起到△D′EC的位置，使二面角D′—EC—B是直二面角.‎ ‎ （1）证明：BE⊥C D′；‎ ‎ （2）求二面角D′—BC—E的正切值. ‎ ‎ ‎ 高三数学章节训练题36《点、直线、平面之间的位置关系》答案 ‎ 一、选择题 ‎ ‎1.C 正四棱柱的底面积为，正四棱柱的底面的边长为，正四棱柱的底面的对角线为，正四棱柱的对角线为，而球的直径等于正四棱柱的对角线，‎ 即， ‎ ‎2.D 取的中点，则则与所成的角 ‎3.C 此时三个平面两两相交，且有三条平行的交线 ‎4.C 利用三棱锥的体积变换：，则 ‎5.B ‎ ‎6. D 一组对边平行就决定了共面；同一平面的两条垂线互相平行，因而共面；‎ ‎ 这些直线都在同一个平面内即直线的垂面；把书本的书脊垂直放在桌上就明确了 二、填空题 ‎1． 分上、中、下三个部分，每个部分分空间为个部分，共部分 ‎2．异面直线；平行四边形；；；且 ‎3． ‎ ‎4． 注意在底面的射影是斜边的中点 ‎ A B C D E F M H G ‎5．‎ 三、解答题 ‎ ‎1、方法一：‎ ‎(1) 证法一：取的中点，连.‎ ‎∵为的中点，∴且. …………1分 ‎∵平面，平面， ‎ ‎∴，∴. …………2分 又，∴. …………3分 ‎∴四边形为平行四边形，则. …………4分 ‎ ∵平面，平面，‎ ‎∴平面. …………5分 证法二：取的中点，连.‎ ‎∵为的中点，∴. …………1分 ‎ ‎∵平面，平面，∴. …………2分 又，‎ ‎∴四边形为平行四边形，则. …………3分 ‎∵平面，平面，‎ ‎∴平面，平面.‎ 又，∴平面平面. …………4分 ‎ ∵平面，‎ ‎∴平面. …………5分 ‎(2) 证：∵为等边三角形，为的中点，∴. …………6分 ‎∵平面，平面，∴. …………7分 又，故平面. …………8分 ‎∵，∴平面. …………9分 ‎∵平面，‎ ‎∴平面平面. …………10分(3) ‎ 解：在平面内，过作于，连.‎ ‎ ∵平面平面， ∴平面.‎ ‎∴为和平面所成的角. …………12分 设，则，‎ ‎，‎ R t△中，.‎ ‎∴直线和平面所成角的正弦值为. …………14分 方法二：‎ 设，建立如图所示的坐标系，则 ‎.…………2分 ‎∵为的中点，∴. …………3分 ‎ (1) 证：， …………4分 ‎∵，平面，∴平面. …………5分 ‎ (2) 证：∵， …………6分 ‎∴，∴. …………8分 ‎∴平面，又平面，‎ ‎∴平面平面. …………10分 ‎ (3) 解：设平面的法向量为，由可得：‎ ‎ ，取. …………12分 ‎ 又，设和平面所成的角为，则 ‎ .‎ ‎∴直线和平面所成角的正弦值为. …………14分 ‎2、解：（1）∵AD=2AB=2，E是AD的中点，‎ ‎ ∴△BAE，△CDE是等腰直角三角形，‎ 易知, ∠BEC=90°，即BE⊥EC.‎ ‎ 又∵平面D′EC⊥平面BEC，面D′EC∩面BEC=EC,‎ ‎ ∴BE⊥面D′EC，又C D′Ì 面D′EC , ∴BE⊥CD′；‎ ‎ （2）法一：设M是线段EC的中点，过M作MF⊥BC ‎ 垂足为F，连接D′M，D′F，则D′M⊥EC. ‎ ‎ ∵平面D′EC⊥平面BEC,‎ ‎ ∴D′M⊥平面EBC, ‎ ‎ ∴MF是D′F在平面BEC上的射影，由三垂线定理得：‎ ‎ D′F⊥BC ‎ ∴∠D′FM是二面D′—BC—E的平面角.‎ ‎ 在Rt△D′MF中，D′M=EC=，MF=AB=‎ ‎ ∴‎ ‎ 即二面角D′—BC—E的正切值为.‎ ‎ 法二：如图，以EB，EC为x轴、y轴，过E垂直于平面BEC的射线为z轴，建立空间直角坐标系.‎ ‎ 则B（，0，0），C（0，，0），D′（0，，） ‎ ‎ 设平面BEC的法向量为；平面D′BC的法向量为 ‎ ‎ ‎ Þ tan= ∴二面角D′—BC—E的正切值为.‎