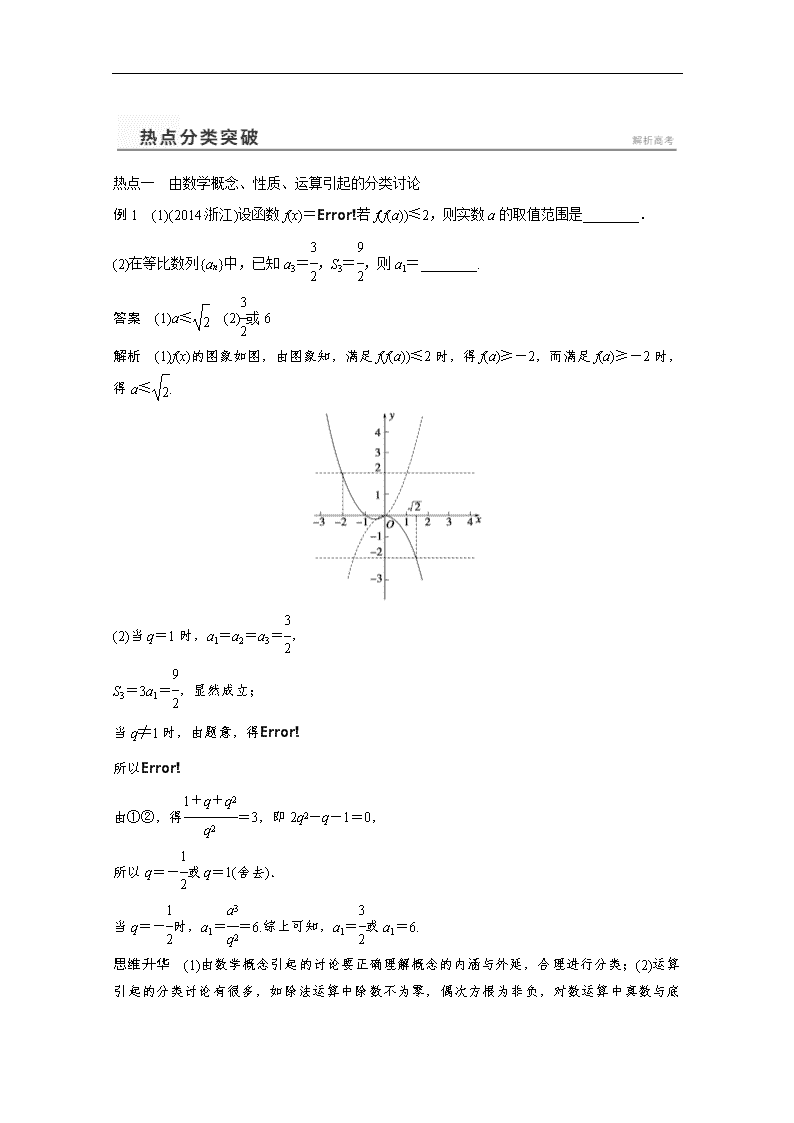2015届高考数学二轮专题训练：专题八 第3讲 分类讨论思想 10页

第3讲　分类讨论思想 ‎1．分类讨论思想是一种重要的数学思想方法．其基本思路是将一个较复杂的数学问题分解(或分割)成若干个基础性问题，通过对基础性问题的解答来实现解决原问题的思想策略．对问题实行分类与整合，分类标准等于增加一个已知条件，实现了有效增设，将大问题(或综合性问题)分解为小问题(或基础性问题)，优化解题思路，降低问题难度．‎ ‎2．分类讨论的常见类型 ‎(1)由数学概念引起的分类讨论．有的概念本身是分类的，如绝对值、直线斜率、指数函数、对数函数等．‎ ‎(2)由性质、定理、公式的限制引起的分类讨论．有的数学定理、公式、性质是分类给出的，在不同的条件下结论不一致，如等比数列的前n项和公式、函数的单调性等．‎ ‎(3)由数学运算要求引起的分类讨论．如除法运算中除数不为零，偶次方根为非负，对数真数与底数的要求，指数运算中底数的要求，不等式两边同乘以一个正数、负数，三角函数的定义域等．‎ ‎(4)由图形的不确定性引起的分类讨论．有的图形类型、位置需要分类：如角的终边所在的象限；点、线、面的位置关系等．‎ ‎(5)由参数的变化引起的分类讨论．某些含有参数的问题，如含参数的方程、不等式，由于参数的取值不同会导致所得结果不同，或对于不同的参数值要运用不同的求解或证明方法．‎ ‎(6)由实际意义引起的讨论．此类问题在应用题中，特别是在解决排列、组合中的计数问题时常用．‎ ‎3．分类讨论的原则 ‎(1)不重不漏．‎ ‎(2)标准要统一，层次要分明．‎ ‎(3)能不分类的要尽量避免或尽量推迟，决不无原则地讨论．‎ ‎4．解分类问题的步骤 ‎(1)确定分类讨论的对象，即对哪个变量或参数进行分类讨论．‎ ‎(2)对所讨论的对象进行合理的分类．‎ ‎(3)逐类讨论，即对各类问题详细讨论，逐步解决．‎ ‎(4)归纳总结，将各类情况总结归纳.‎ 热点一　由数学概念、性质、运算引起的分类讨论 例1　(1)(2014·浙江)设函数f(x)＝若f(f(a))≤2，则实数a的取值范围是________．‎ ‎(2)在等比数列{an}中，已知a3＝，S3＝，则a1＝________.‎ 答案　(1)a≤　(2)或6‎ 解析　(1)f(x)的图象如图，由图象知，满足f(f(a))≤2时，得f(a)≥－2，而满足f(a)≥－2时，得a≤.‎ ‎(2)当q＝1时，a1＝a2＝a3＝，‎ S3＝3a1＝，显然成立；‎ 当q≠1时，由题意，得 所以 由①②，得＝3，即2q2－q－1＝0，‎ 所以q＝－或q＝1(舍去)．‎ 当q＝－时，a1＝＝6.综上可知，a1＝或a1＝6.‎ 思维升华　(1)由数学概念引起的讨论要正确理解概念的内涵与外延，合理进行分类；(2)运算引起的分类讨论有很多，如除法运算中除数不为零，偶次方根为非负，对数运算中真数与底数的要求，指数运算中底数的要求，不等式两边同乘以一个正数、负数，三角函数的定义域等．‎ ‎　(1)已知函数f(x)＝满足f(a)＝3，则f(a－5)的值为(　　)‎ A．log23 B. C. D．1‎ ‎(2)已知数列{an}的前n项和Sn＝pn－1(p是常数)，则数列{an}是(　　)‎ A．等差数列 B．等比数列 C．等差数列或等比数列 D．以上都不对 答案　(1)C　(2)D 解析　(1)分两种情况分析，①或者②，①无解，由②得，a＝7，所以f(a－5)＝22－3＋1＝，故选C.‎ ‎(2)∵Sn＝pn－1，‎ ‎∴a1＝p－1，an＝Sn－Sn－1＝(p－1)pn－1(n≥2)，‎ 当p≠1且p≠0时，{an}是等比数列；‎ 当p＝1时，{an}是等差数列；‎ 当p＝0时，a1＝－1，an＝0(n≥2)，此时{an}既不是等差数列也不是等比数列．‎ 热点二　由图形位置或形状引起的讨论 例2　(1)不等式组表示的平面区域内有________个整点(把横、纵坐标都是整数的点称为整点)．‎ ‎(2)设圆锥曲线T的两个焦点分别为F1，F2，若曲线T上存在点P满足|PF1|∶|F1F2|∶|PF2|＝4∶3∶2，则曲线T的离心率为________．‎ 答案　(1)20　(2)或 解析　(1)画出不等式组表示的平面区域(如图)．‎ 结合图中的可行域可知 x∈[－，2]，y∈[－2,5]．‎ 由图形及不等式组，知 当x＝－1时，1≤y≤2，有2个整点；‎ 当x＝0时，0≤y≤3，有4个整点；‎ 当x＝1时，－1≤y≤4，有6个整点；‎ 当x＝2时，－2≤y≤5，有8个整点；‎ 所以平面区域内的整点共有2＋4＋6＋8＝20(个)．‎ ‎(2)不妨设|PF1|＝4t，|F1F2|＝3t，|PF2|＝2t，若该圆锥曲线为椭圆，则有|PF1|＋|PF2|＝6t＝2a，|F1F2‎ ‎|＝3t＝2c，e＝＝＝＝；若该圆锥曲线是双曲线，则有|PF1|－|PF2|＝2t＝2a，‎ ‎|F1F2|＝3t＝2c，e＝＝＝＝.‎ 所以圆锥曲线T的离心率为或.‎ 思维升华　求解有关几何问题时，由于几何元素的形状、位置变化的不确定性，所以需要根据图形的特征进行分类讨论．‎ 一般由图形的位置或形状变化引发的讨论包括：二次函数对称轴位置的变化；函数问题中区间的变化；函数图象形状的变化；直线由斜率引起的位置变化；圆锥曲线由焦点引起的位置变化或由离心率引起的形状变化．‎ ‎　(1)已知变量x，y满足的不等式组表示的是一个直角三角形围成的平面区域，则实数k等于(　　)‎ A．－ B. C．0 D．－或0‎ ‎(2)设F1，F2为椭圆＋＝1的两个焦点，P为椭圆上一点．已知P，F1，F2是一个直角三角形的三个顶点，且|PF1|>|PF2|，则的值为________．‎ 答案　(1)D　(2)2或 解析　(1)不等式组表示的可行域如图(阴影部分)所示，由图可知若不等式组表示的平面区域是直角三角形，只有直线y＝kx＋1与直线x＝0垂直(如图①)或直线y＝kx＋1与直线y＝2x垂直(如图②)时，平面区域才是直角三角形．‎ 由图形可知斜率k的值为0或－.‎ ‎(2)若∠PF2F1＝90°，‎ 则|PF1|2＝|PF2|2＋|F1F2|2，‎ ‎∵|PF1|＋|PF2|＝6，|F1F2|＝2，‎ 解得|PF1|＝，|PF2|＝，∴＝.‎ 若∠F2PF1＝90°，‎ 则|F1F2|2＝|PF1|2＋|PF2|2‎ ‎＝|PF1|2＋(6－|PF1|)2，‎ 解得|PF1|＝4，|PF2|＝2，‎ ‎∴＝2.综上所述，＝2或.‎ 热点三　由参数引起的分类讨论 例3　(2014·四川改编)已知函数f(x)＝ex－ax2－bx－1，其中a，b∈R，e＝2.718 28…为自然对数的底数．‎ 设g(x)是函数f(x)的导函数，求函数g(x)在区间[0,1]上的最小值．‎ 解　由f(x)＝ex－ax2－bx－1，‎ 有g(x)＝f′(x)＝ex－2ax－b.‎ 所以g′(x)＝ex－2a.‎ 因此，当x∈[0,1]时，g′(x)∈[1－2a，e－2a]．‎ 当a≤时，g′(x)≥0，‎ 所以g(x)在[0,1]上单调递增，‎ 因此g(x)在[0,1]上的最小值是g(0)＝1－b；‎ 当a≥时，g′(x)≤0，所以g(x)在[0,1]上单调递减，‎ 因此g(x)在[0,1]上的最小值是g(1)＝e－2a－b；‎ 当－1)，‎ 所以f′(x)＝＋＝.‎ ‎①当a≥0时，因为x>－1，所以f′(x)>0，‎ 故f(x)在(－1，＋∞)上单调递增．‎ ‎②当a<0时，由得－1－1－a，‎ 故f(x)在(－1－a，＋∞)上单调递增．‎ 综上，当a≥0时，函数f(x)在(－1，＋∞)上单调递增；‎ 当a<0时，函数f(x)在(－1，－1－a)上单调递减，‎ 在(－1－a，＋∞)上单调递增．‎ 分类讨论思想的本质是“化整为零，积零为整”．用分类讨论的思维策略解数学问题的操作过程：明确讨论的对象和动机→确定分类的标准→逐类进行讨论→归纳综合结论→检验分类是否完备(即分类对象彼此交集为空集，并集为全集)．做到“确定对象的全体，明确分类的标准，分类不重复、不遗漏”的分析讨论．‎ 常见的分类讨论问题有：‎ ‎(1)集合：注意集合中空集∅的讨论．‎ ‎(2)函数：对数函数或指数函数中的底数a，一般应分a>1和01的讨论；等比数列中分公比q＝1和q≠1的讨论．‎ ‎(4)三角函数：角的象限及函数值范围的讨论．‎ ‎(5)不等式：解不等式时含参数的讨论，基本不等式相等条件是否满足的讨论．‎ ‎(6)立体几何：点线面及图形位置关系的不确定性引起的讨论；‎ ‎(7)平面解析几何：直线点斜式中k分存在和不存在，直线截距式中分b＝0和b≠0的讨论；轨迹方程中含参数时曲线类型及形状的讨论．‎ ‎(8)排列、组合、概率中的分类计数问题．‎ ‎(9)去绝对值时的讨论及分段函数的讨论等．‎ 真题感悟 ‎1．(2014·课标全国Ⅱ)钝角三角形ABC的面积是，AB＝1，BC＝，则AC等于(　　)‎ A．5 B. C．2 D．1‎ 答案　B 解析　∵S△ABC＝AB·BC·sin B＝×1×sin B＝，‎ ‎∴sin B＝，∴B＝或.‎ 当B＝时，根据余弦定理有AC2＝AB2＋BC2－2AB·BC·cos B＝1＋2＋2＝5，所以AC＝，此时△ABC为钝角三角形，符合题意；‎ 当B＝时，根据余弦定理有AC2＝AB2＋BC2－2AB·BC·cos B＝1＋2－2＝1，所以AC＝1，此时AB2＋AC2＝BC2，△ABC为直角三角形，不符合题意．故AC＝.‎ ‎2．(2013·安徽)“a≤0”是“函数f(x)＝|(ax－1)x|在区间(0，＋∞)内单调递增”的(　　)‎ A．充分不必要条件 B．必要不充分条件 C．充分必要条件 D．既不充分也不必要条件 答案　C 解析　当a＝0时，f(x)＝|(ax－1)x|＝|x|在区间(0，＋∞)上单调递增；‎ 当a<0时，结合函数f(x)＝|(ax－1)x|＝|ax2－x|的图象知函数在(0，＋∞)上单调递增，如图(1)所示；‎ 当a>0时，结合函数f(x)＝|(ax－1)x|＝|ax2－x|的图象知函数在(0，＋∞‎ ‎)上先增后减再增，不符合条件，如图(2)所示．‎ 所以，要使函数f(x)＝|(ax－1)x|在(0，＋∞)上单调递增只需a≤0.‎ 即“a≤0”是“函数f(x)＝|(ax－1)x|在区间(0，＋∞)内单调递增”的充要条件．‎ ‎3．(2014·广东)设集合A＝{(x1，x2，x3，x4，x5)|xi∈{－1,0,1}，i＝1,2,3,4,5}，那么集合A中满足条件“1≤|x1|＋|x2|＋|x3|＋|x4|＋|x5|≤3”的元素个数为(　　)‎ A．60 B．90‎ C．120 D．130‎ 答案　D 解析　在x1，x2，x3，x4，x5这五个数中，因为xi∈{－1,0,1}，i＝1,2,3,4,5，所以满足条件1≤|x1|＋|x2|＋|x3|＋|x4|＋|x5|≤3的可能情况有“①一个1(或－1)，四个0，有C×2种；②两个1(或－1)，三个0，有C×2种；③一个－1，一个1，三个0，有A种；④两个1(或－1)，一个－1(或1)，两个0，有CC×2种；⑤三个1(或－1)，两个0，有C×2种．故共有C×2＋C×2＋A＋CC×2＋C×2＝130(种)，故选D.‎ 押题精练 ‎1．已知函数f(x)＝为R上的单调函数，则实数a的取值范围是(　　)‎ A．(0，＋∞) B．[－2,0)‎ C．[－1,0) D．[－1，＋∞)‎ 答案　C 解析　若a＝0，则f(x)在定义域的两个区间内都是常函数，不具备单调性；若a>0，函数f(x)在两段上都是单调递增的，要使函数在R上单调递增，只要(a＋2)e0≤1，即a≤－1，与a>0矛盾，此时无解．若－20)的焦点为F，P为其上的一点，O为坐标原点，若△OPF为等腰三角形，则这样的点P的个数为(　　)‎ A．2 B．3 C．4 D．6‎ 答案　C 解析　当|PO|＝|PF|时，点P在线段OF的中垂线上，此时，点P的位置有两个；当|OP|＝|OF|时，点P的位置也有两个；对|FO|＝|FP|的情形，点P不存在．事实上，F(p,0)，若设P(x，y)，则|FO|＝p，|FP|＝，若＝p，则有x2－2px＋y2＝0，又∵y2＝4px，∴x2＋2px＝0，解得x＝0或x＝－2p，当x＝0时，不构成三角形．当x＝－2p(p>0)时，与点P在抛物线上矛盾．所以符合要求的点P一共有4个．‎ ‎4．6位同学在毕业聚会活动中进行纪念品的交换，任意两位同学之间最多交换一次，进行交换的两位同学互赠一份纪念品．已知6位同学之间共进行了13次交换，则收到4份纪念品的同学人数为(　　)‎ A．1或3 B．1或4‎ C．2或3 D．2或4‎ 答案　D 解析　设6位同学分别用a，b，c，d，e，f表示．‎ 若任意两位同学之间都进行交换共进行15次交换，现共进行了13次交换，说明有两次交换没有发生，此时可能有两种情况：‎ ‎(1)由3人构成的2次交换，如a－b和a－c之间的交换没有发生，则收到4份纪念品的有b，c两人．‎ ‎(2)由4人构成的2次交换，如a－b和c－e之间的交换没有发生，则收到4份纪念品的有a，b，c，e四人．故选D.‎ ‎5．已知等差数列{an}的前3项和为6，前8项和为－4.‎ ‎(1)求数列{an}的通项公式；‎ ‎(2)设bn＝(4－an)qn－1 (q≠0，n∈N*)，求数列{bn}的前n项和Sn.‎ 解　(1)设数列{an}的公差为d，‎ 由已知，得解得 故an＝3－(n－1)＝4－n.‎ ‎(2)由(1)可得bn＝n·qn－1，‎ 于是Sn＝1·q0＋2·q1＋3·q2＋…＋n·qn－1.‎ 若q≠1，将上式两边同乘q，得 qSn＝1·q1＋2·q2＋…＋(n－1)·qn－1＋n·qn.‎ 两式相减，得(q－1)Sn＝nqn－1－q1－q2－…－qn－1‎ ‎＝nqn－＝.‎ 于是，Sn＝.‎ 若q＝1，则Sn＝1＋2＋3＋…＋n＝.‎ 综上，Sn＝ ‎6．已知函数f(x)＝(a＋1)ln x＋ax2＋1，试讨论函数f(x)的单调性．‎ 解　由题意知f(x)的定义域为(0，＋∞)，‎ f′(x)＝＋2ax＝.‎ ‎①当a≥0时，f′(x)>0，故f(x)在(0，＋∞)上单调递增．‎ ‎②当a≤－1时，f′(x)<0，故f(x)在(0，＋∞)上单调递减．‎ ‎③当－10；‎ 当x∈时，f′(x)<0.‎ 故f(x)在上单调递增，‎ 在上单调递减．‎ 综上，当a≥0时，f(x)在(0，＋∞)上单调递增；‎ 当a≤－1时，f(x)在(0，＋∞)上单调递减；‎ 当－1