高考数学一轮复习第九章立体几何9-2空间图形的基本关系与公理练习理北师大版 8页

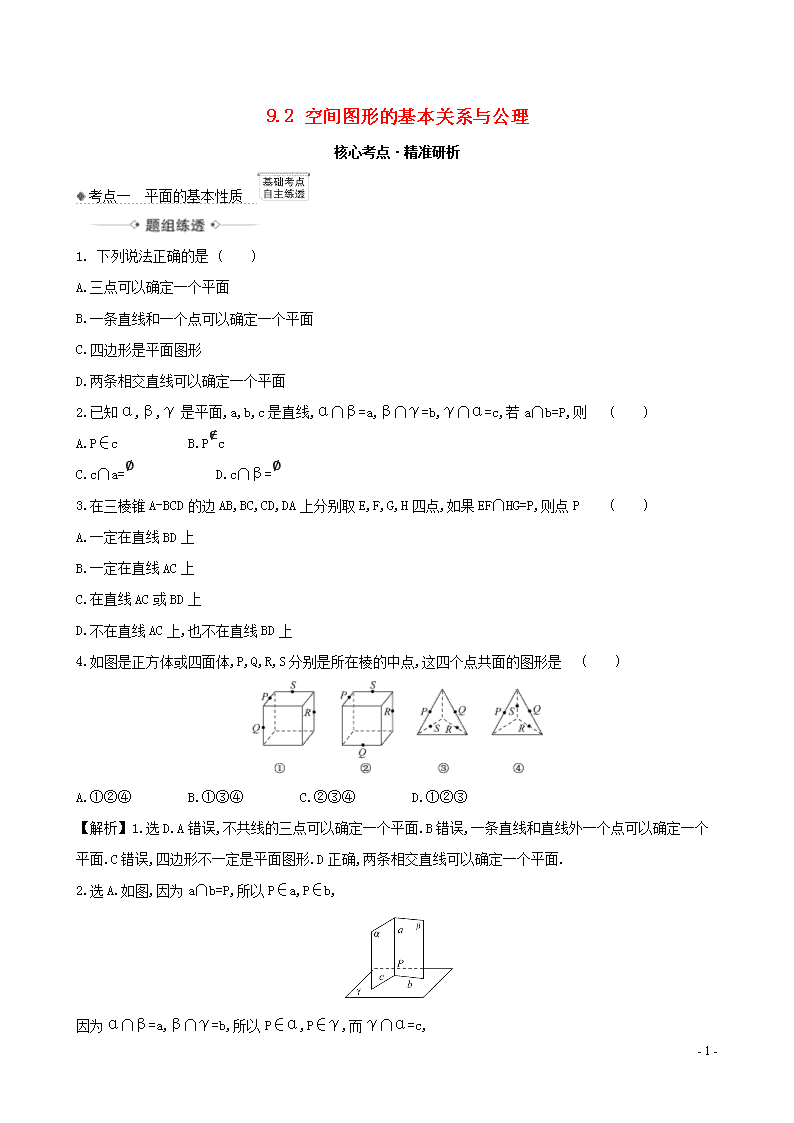
‎9.2 空间图形的基本关系与公理 核心考点·精准研析 考点一　平面的基本性质 ‎ ‎1. 下列说法正确的是 (　　)‎ A.三点可以确定一个平面 B.一条直线和一个点可以确定一个平面 C.四边形是平面图形 D.两条相交直线可以确定一个平面 ‎2.已知α,β,γ是平面,a,b,c是直线,α∩β=a,β∩γ=b,γ∩α=c,若a∩b=P,则 (　　)‎ A.P∈c B.P∉c C.c∩a=∅ D.c∩β=∅‎ ‎3.在三棱锥A-BCD的边AB,BC,CD,DA上分别取E,F,G,H四点,如果EF∩HG=P,则点P (　　)‎ A.一定在直线BD上 B.一定在直线AC上 C.在直线AC或BD上 D.不在直线AC上,也不在直线BD上 ‎4.如图是正方体或四面体,P,Q,R,S分别是所在棱的中点,这四个点共面的图形是 (　　)‎ A.①②④ B.①③④ C.②③④ D.①②③‎ ‎【解析】1.选D.A错误,不共线的三点可以确定一个平面.B错误,一条直线和直线外一个点可以确定一个平面.C错误,四边形不一定是平面图形.D正确,两条相交直线可以确定一个平面.‎ ‎2.选A.如图,因为a∩b=P,所以P∈a,P∈b,‎ 因为α∩β=a,β∩γ=b,所以P∈α,P∈γ,而γ∩α=c,‎ - 8 -‎ 所以P∈c.‎ ‎3.选B.如图所示,‎ 因为EF 平面ABC,HG 平面ACD,‎ EF∩HG=P,所以P∈平面ABC,P∈平面ACD.‎ 又因为平面ABC∩平面ACD=AC,所以P∈AC.‎ ‎4.选D.在图①中分别连接PS,QR,易证PS∥QR,所以P,Q,R,S四点共面;在图中③分别连接PQ,RS,易证PQ∥RS,所以P,Q,R,S共面.在②图中过点P,Q,R,S可作一正六边形,故四点共面;在图④中PS与QR为异面直线,所以四点不共面.‎ ‎　共面、共线、共点问题的证明 ‎(1)证明共面的方法:①先确定一个平面,然后再证其余的线(或点)在这个平面内;②证两平面重合.‎ ‎(2)证明共线的方法:①先由两点确定一条直线,再证其他各点都在这条直线上;②直接证明这些点都在同一条特定直线上.‎ ‎(3)证明线共点问题的常用方法是:先证其中两条直线交于一点,再证其他直线经过该点.‎ ‎【秒杀绝招】‎ 排除法解T4,在图④中PS与QR为异面直线,所以四点不共面,可排除A,B,C,直接选D.‎ 考点二　异面直线所成的角 ‎ ‎【典例】‎ ‎1.(2018·全国卷II)在正方体ABCD-A1B1C1D1中,E为棱CC1的中点,则异面直线AE与CD所成角的正切值为 (　　)‎ A. B. C. D.‎ ‎2.已知直三棱柱ABC-A1B1C1中,∠ABC=120°,AB=2,BC=CC1=1,则异面直线AB1与BC1所成角的余弦值为 (　　)‎ A. B. C. 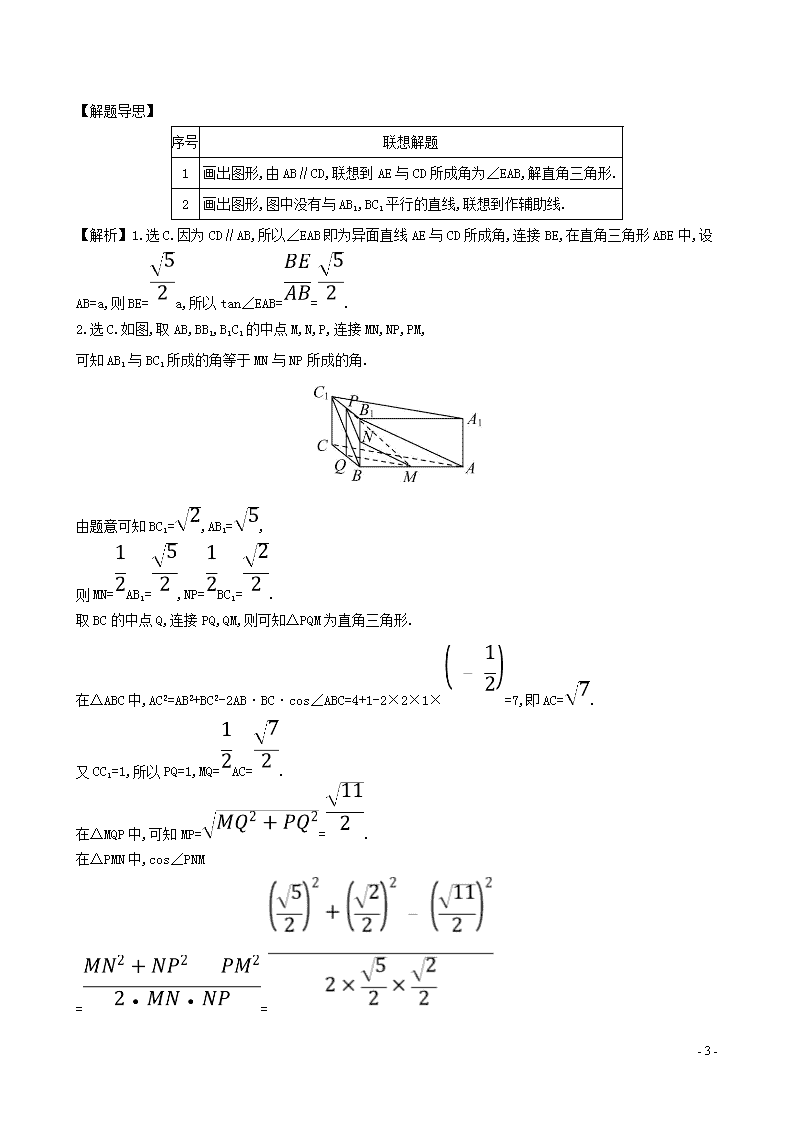D.‎ - 8 -‎ ‎【解题导思】‎ 序号 联想解题 ‎1‎ 画出图形,由AB∥CD,联想到AE与CD所成角为∠EAB,解直角三角形.‎ ‎2‎ 画出图形,图中没有与AB1,BC1平行的直线,联想到作辅助线.‎ ‎【解析】1.选C.因为CD∥AB,所以∠EAB即为异面直线AE与CD所成角,连接BE,在直角三角形ABE中,设AB=a,则BE=a,所以tan∠EAB==.‎ ‎2.选C.如图,取AB,BB1,B1C1的中点M,N,P,连接MN,NP,PM,‎ 可知AB1与BC1所成的角等于MN与NP所成的角.‎ 由题意可知BC1=,AB1=,‎ 则MN=AB1=,NP=BC1=.‎ 取BC的中点Q,连接PQ,QM,则可知△PQM为直角三角形.‎ 在△ABC中,AC2=AB2+BC2-2AB·BC·cos∠ABC=4+1-2×2×1×=7,即AC=.‎ 又CC1=1,所以PQ=1,MQ=AC=.‎ 在△MQP中,可知MP==.‎ 在△PMN中,cos∠PNM ‎==‎ - 8 -‎ ‎=-,‎ 又异面直线所成角的范围为,‎ 故所求角的余弦值为.‎ ‎【一题多解】选C.把三棱柱ABC-A1B1C1补成四棱柱ABCD-A1B1C1D1,如图,‎ 连接C1D,BD,则AB1与BC1所成的角为∠BC1D(或其补角).‎ 由题意可知BC1=,‎ BD==,C1D=AB1=.可知B+BD2=C1D2,‎ 所以cos∠BC1D==.‎ ‎　求异面直线所成的角的三个步骤 ‎(1)一作:根据定义作平行线,作出异面直线所成的角.‎ ‎(2)二证:证明作出的角是异面直线所成的角.‎ ‎(3)三求:解三角形,求出所作的角.‎ ‎1.直三棱柱ABC-A1B1C1中,若∠BAC=90°,AB=AC=AA1,则异面直线BA1与AC1所成的角等于 (　　)‎ A.30° B.45° C.60° D.90°‎ ‎【解析】选C.如图,可补成一个正方体,‎ 所以AC1∥BD1.‎ - 8 -‎ 所以BA1与AC1所成的角为∠A1BD1.‎ 又易知△A1BD1为正三角形,‎ 所以∠A1BD1=60°.即BA1与AC1成60°的角.‎ ‎2.如图,已知圆柱的轴截面ABB1A1是正方形,C是圆柱下底面弧AB的中点,C1是圆柱上底面弧A1B1的中点,那么异面直线AC1与BC所成角的正切值为　　　　. ‎ ‎【解析】取圆柱下底面弧AB的另一中点D,连接C1D,AD,‎ 因为C是圆柱下底面弧AB的中点,‎ 所以AD∥BC,所以直线AC1与AD所成的角即为异面直线AC1与BC所成的角,因为C1是圆柱上底面弧A1B1的中点,所以C1D垂直于圆柱下底面,所以C1D⊥AD.‎ 因为圆柱的轴截面ABB1A1是正方形,‎ 所以C1D=AD,‎ 所以直线AC1与AD所成角的正切值为,‎ 所以异面直线AC1与BC所成角的正切值为.‎ 答案:‎ 考点三　空间两条直线的位置关系 ‎ 命 题 精 解 读 ‎1.考什么:(1)考查异面直线的判断,直线平行、垂直的判断等问题.(2)考查直观想象的核心素养.‎ ‎2.怎么考:以柱、锥、台、球及组合体为载体,考查直线位置关系的判断.‎ ‎3.新趋势:以异面直线、平行直线为载体考查点的不共面与共面问题.‎ - 8 -‎ 学 霸 好 方 法 ‎1.直线位置关系的判断方法:‎ 异面直线可采用直接法或反证法;平行直线可利用三角形(梯形)中位线的性质、公理4及线面平行与面面平行的性质定理;垂直关系往往利用线面垂直或面面垂直的性质来解决.‎ ‎2.交汇问题:与线面、面面平行与垂直相结合命题.‎ 两条异面直线的判定 ‎【典例】在图中,G,N,M,H分别是正三棱柱(两底面为正三角形的直棱柱)的顶点或所在棱的中点,则表示直线GH、MN是异面直线的图形有　　　　.(填上所有正确答案的序号) ‎ ‎【解析】图①中,直线GH∥MN;‎ 图②中,G,H,N三点共面,但M∉面GHN,‎ 因此直线GH与MN异面;‎ 图③中,连接MG,GM∥HN,因此GH与MN共面;‎ 图④中,G,M,N三点共面,但H∉面GMN,‎ 因此GH与MN异面,所以图②④中GH与MN异面.‎ 答案:②④‎ 两直线平行或相交的判定 ‎【典例】已知空间四边形ABCD中,E,H分别是边AB,AD的中点,F,G分别是边BC,CD的中点.‎ 求证:EG与FH相交. ‎ ‎【证明】如图,连接AC,BD,则EF∥AC,HG∥AC,‎ 因此EF∥HG;同理EH∥FG,则EFGH为平行四边形.又EG,FH是▱EFGH的对角线,所以EG与HF相交.‎ - 8 -‎ ‎1.若两条直线是异面直线,则称为一对异面直线,则从正方体的12条棱中任取两条,共有　　　对异面直线 (　　) ‎ A.48 B.36 C.24 D.12‎ ‎【解析】选C.每一条棱所在的直线与其余的棱所在的直线成异面直线的有4对,所以共有4×12=48对,但是这48对中每一种都重复了一对,所以所求的异面直线共有24对.‎ ‎2.如图所示,正方体ABCD-A1B1C1D1中,M,N分别为棱C1D1,C1C的中点,有以下四个结论:‎ ‎①直线AM与CC1是相交直线;‎ ‎②直线AM与BN是平行直线;‎ ‎③直线BN与MB1是异面直线;‎ ‎④直线AM与DD1是异面直线.‎ 其中正确的结论为　　　　.(注:把你认为正确的结论序号都填上) ‎ ‎【解析】因为点A在平面CDD1C1外,点M在平面CDD1C1内,直线CC1在平面CDD1C1内,CC1不过点M,所以AM与CC1是异面直线,故①错;取DD1中点E,连接AE,则BN∥AE,但AE与AM相交,故②错;因为点B1与BN都在平面BCC1B1内,点M在平面BCC1B1外,BN不过点B1,所以BN与MB1是异面直线,故③正确;同理④正确,故填③④.‎ 答案:③④‎ ‎1.若直线l1和l2是异面直线,l1在平面α内,l2在平面β内,l是平面α与平面β的交线,则下列说法正确的是 (　　)‎ A.l与l1,l2都不相交 B.l与l1,l2都相交 C.l至多与l1,l2中的一条相交 D.l至少与l1,l2中的一条相交 ‎【解析】选D.由直线l1和l2是异面直线可知l1与l2不平行,故l1,l2中至少有一条与l相交.‎ ‎2.如图,三棱柱ABC-A1B1C1中,底面三角形A1B1C1是正三角形,E是BC的中点,则下列叙述正确的是 (　　)‎ - 8 -‎ A.CC1与B1E是异面直线 B.C1C与AE共面 C.AE与B1C1是异面直线 D.AE与B1C1所成的角为60°‎ ‎【解析】选C.由于CC1与B1E都在平面C1B1BC内,故C1C与B1E是共面的,所以A错误;由于C1C在平面C1B1BC内,而AE与平面C1B1BC相交于E点,点E不在C1C上,故C1C与AE是异面直线,B错误;同理AE与B1C1是异面直线,C正确;而AE与B1C1所成的角就是AE与BC所成的角,E为BC中点,△ABC为正三角形,所以AE⊥BC,D错误.‎ - 8 -‎