2020_2021学年新教材高中数学第一章空间向量与立体几何章末整合课件新人教A版选择性必修第一册 37页

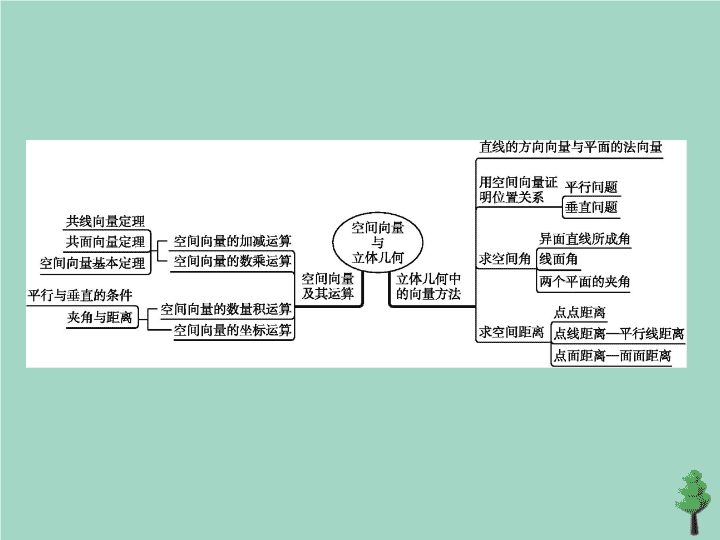
章末整合 专题一 　 应用空间向量证明位置关系   例 1 如图所示 , 已知 PA ⊥ 平面 ABCD , 四边形 ABCD 为矩形 , PA=AD , M , N 分别为 AB , PC 的中点 . 求证 :(1) MN ∥ 平面 PAD ; (2) 平面 PMC ⊥ 平面 PDC. 证明 : (1) 如图所示 , 以 A 为坐标原点 , AB , AD , AP 所在直线为 x , y , z 轴建立空间直角坐标系 A-xyz. 设 PA=AD=a , AB=b , 则有 P (0,0, a ), A (0,0,0), D (0, a ,0), C ( b , a ,0), B ( b ,0,0) . ∵ M , N 分别为 AB , PC 的中点 , 方法技巧 利用空间向量证明平行、垂直关系的方法 (1) 证明两条直线平行 , 只需证明两条直线的方向向量是共线向量即可 . (2) 证明线面平行的方法 : ① 证明直线的方向向量与平面的法向量垂直 ; ② 证明可在平面内找到一个向量与直线的方向向量是共线向量 ; ③ 利用共面向量定理 , 即证明可在平面内找到两个不共线向量来线性表示直线的方向向量 . (3) 证明面面平行的方法 : ① 证明两个平面的法向量平行 ( 即是共线向量 ); ② 转化为线面平行、线线平行问题 . (4) 证明两条直线垂直 , 只需证明两直线的方向向量垂直 . (5) 证明线面垂直的方法 : ① 证明直线的方向向量与平面的法向量平行 ; ② 转化为线线垂直问题 . (6) 证明面面垂直的方法 : ① 证明两个平面的法向量互相垂直 ; ② 转化为线面垂直、线线垂直问题 . 变式训练 1 如图 , 正三棱柱 ABC-A 1 B 1 C 1 的所有侧棱长及底面边长都为 2, D 为 CC 1 的中点 . 求证 : AB 1 ⊥ 平面 A 1 BD. 证法三 : 如图 , 取 BC , B 1 C 1 的中点 O , O 1 , 连接 AO , OO 1 . 因为 △ ABC 为正三角形 , 所以 AO ⊥ BC. 因为在正三棱柱 ABC-A 1 B 1 C 1 中 , O , O 1 都为中点 , 所以 OB ⊥ OO 1 . 又平面 ABC ⊥ 平面 BCC 1 B 1 , 所以 AO ⊥ 平面 BCC 1 B 1 , 所以 AO ⊥ OO 1 . 专题二 　 应用空间向量求空间距离   例 2 如图所示的多面体是由底面为 ABCD 的长方体被平面 AEC 1 F 所截而得到的 , 其中 AB= 4, BC= 2, CC 1 = 3, BE= 1 . (1) 求 BF 的长 ; (2) 求点 C 到平面 AEC 1 F 的距离 . 解 : (1) 建立如图所示的空间直角坐标系 , 则 D (0,0,0), B (2,4,0), A (2,0,0), C (0,4,0), E (2,4,1), C 1 (0,4,3) . 设 F (0,0, z ) . 由题意得 AEC 1 F 为平行四边形 , 方法技巧 向量法求点面距离的 步骤 变式训练 2 在棱长为 a 的正方体 ABCD-A 1 B 1 C 1 D 1 中 , E , F 分别是 BB 1 , CC 1 的中点 . (1) 求证 : AD ∥ 平面 A 1 EFD 1 ; (2) 求直线 AD 与平面 A 1 EFD 1 的距离 . 证明 : (1) 如图 , 以点 D 为坐标原点 , DA , DC , DD 1 所在直线分别为 x 轴 , y 轴 , z 轴 , 建立空间直角坐标系 D-xyz , 则 又 D 1 A 1 ⊂ 平面 A 1 EFD 1 , DA ⊄ 平面 A 1 EFD 1 , 所以 DA ∥ 平面 A 1 EFD 1 . 专题三 　 应用空间向量求空间角   例 3 如图 , 在长方体 ABCD-A 1 B 1 C 1 D 1 中 , AB= 5, AD= 8, AA 1 = 4, M 为 B 1 C 1 上一点且 B 1 M= 2, 点 N 在线段 A 1 D 上 , A 1 D ⊥ AN. (1) 求异面直线 A 1 D 与 AM 所成的角 ; (2) 求直线 AD 与平面 ANM 所成角 θ 的正弦值 ; (3) 求平面 ANM 与平面 ABCD 夹角的余弦值 . 解 : 以 A 为原点 , 分别以 AB , AD , AA 1 所在直线为 x 轴、 y 轴、 z 轴建立如图所示的空间直角坐标系 , 则 A (0,0,0), B (5,0,0), D (0,8,0), A 1 (0,0,4), M (5,2,4) . 方法技巧 向量法求线面角、两平面夹角的方法 (1) 利用空间向量求直线与平面所成的角的两种方法 : ① 分别求出斜线和它在平面内的射影所在直线的方向向量 , 将问题转化为求两个方向向量的夹角 ( 或其补角 ); ② 通过平面的法向量来求 , 即求出斜线的方向向量与平面的法向量所夹的锐角 , 则其余角就是斜线和平面所成的角 . (2) 利用空间向量求两平面夹角的两种方法 : ① 利用定义 , 分别在二面角的两个半平面内找到与棱垂直且从垂足出发的两个向量 , 则这两个向量的夹角的大小就是二面角的平面角的大小 , 再由此得两平面的夹角 ; ② 通过平面的法向量来求 : 设二面角的两个半平面的法向量分别为 n 1 和 n 2 , 则两平面夹角的大小等于 < n 1 , n 2 > ( 或 π -< n 1 , n 2 > ), 注意取锐角或直角 . 变式训练 3 在四棱锥 P-ABCD 中 , PD ⊥ 底面 ABCD , 底面 ABCD 是直角梯形 , ∠ BAD= ∠ ADC= 90 ° , AB=AD=PD= 2, CD= 4, 点 E 是 PB 的中点 . (1) 求异面直线 AE 与 CP 所成角的余弦值 ; (2) 若点 F ∈ 平面 ABCD , 且 EF ⊥ 平面 PBC , 求点 F 的坐标 ; (3) 求直线 AB 与平面 PBC 所成角的正弦值 . 解 : (1) 如图所示建立空间直角坐标系 D-xyz. 由题意得 A (2,0,0), B (2,2,0), P (0,0,2), C (0,4,0) . ∵ E 为 PB 的中点 , ∴ E (1,1,1), 专题四 　 空间中的折叠与探究性问题   例 4 如图 , 在直三棱柱 ABC-A 1 B 1 C 1 中 , AB=BC= 2 AA 1 , ∠ ABC= 90 ° , D 是 BC 的中点 . (1) 求证 : A 1 B ∥ 平面 ADC 1 ; (2) 求平面 ADC 1 与平面 ABC 夹角的余弦值 ; (3) 线段 A 1 B 1 上是否存在点 E , 使 AE 与 DC 1 成 60 ° 角 ? 若存在 , 确定点 E 的位置 ; 若不存在 , 请说明理由 . (1) 证明 : 连接 A 1 C , 交 AC 1 于点 O , 连接 OD , 如图 . 由于棱柱 ABC-A 1 B 1 C 1 是直三棱柱 , 得四边形 ACC 1 A 1 为矩形 , O 为 A 1 C 的中点 . 又 D 为 BC 的中点 , 所以 OD 为 △ A 1 BC 的中位线 , 所以 A 1 B ∥ OD. 因为 OD ⊂ 平面 ADC 1 , A 1 B ⊄ 平面 ADC 1 , 所以 A 1 B ∥ 平面 ADC 1 . (2) 解 : 由于棱柱 ABC-A 1 B 1 C 1 是直三棱柱 , 且 ∠ ABC= 90 ° , 得 BA , BC , BB 1 两两垂直 , 以 BC , BA , BB 1 所在直线分别为 x , y , z 轴 , 建立如图所示的空间直角坐标系 B-xyz. 设 BA= 2, 则 B (0,0,0), C (2,0,0), A (0,2,0), C 1 (2,0,1), D (1,0,0), (3) 解 : 存在 . 假设存在满足条件的点 E. 因为点 E 在线段 A 1 B 1 上 , A 1 (0,2,1), B 1 (0,0,1), 故可设 E (0, λ ,1), 其中 0 ≤ λ ≤ 2 . 方法技巧 解决存在性问题的基本策略 假设题中的数学对象存在 ( 或结论成立 ), 然后在这个前提下进行逻辑推理 , 若能推导出与条件吻合的数据或事实 , 说明假设成立 , 即存在 , 并可进一步证明 ; 若推导出与条件或实际情况相矛盾的结论 , 则说明假设不成立 , 即不存在 . 变式训练 4 如图 , 在四棱锥 P-ABCD 中 , 平面 PAD ⊥ 平面 ABCD , PA ⊥ PD , PA=PD , AB ⊥ AD , AB= 1, AD= 2, AC=CD= (1) 求证 : PD ⊥ PB. (2) 求直线 PB 与平面 PCD 所成角的正弦值 . (1) 证明 : ∵ 平面 PAD ⊥ 平面 ABCD 于 AD , AB ⊥ AD , ∴ AB ⊥ 平面 PAD , ∴ PD ⊥ AB. 又 ∵ PD ⊥ PA , PA ∩ AB=A , ∴ PD ⊥ 平面 PAB , ∴ PD ⊥ PB. (2) 解 : 如图 , 取 AD 中点为 O , 连接 CO , PO. 例 5 (2020 陕西汉中高二检测 ) 如图 ① , 在等腰梯形 ABCD 中 , AB= 2, CD= 6, AD= 2 , E , F 分别是 CD 的两个三等分点 , 若把等腰梯形沿虚线 AF , BE 折起 , 使得点 C 和点 D 重合 , 记为点 P , 如图 ② . (1) 求证 : 平面 PEF ⊥ 平面 ABEF ; (2) 求平面 PAE 与平面 PAB 夹角的余弦值 . (1) 证明 : ∵ 四边形 ABCD 为等腰梯形 , AB= 2, CD= 6, AD= 2 , E , F 是 CD 的两个三等分点 , ∴ 四边形 ABEF 是正方形 , ∴ BE ⊥ EF. ∵ BE ⊥ PE , 且 PE ∩ EF=E , ∴ BE ⊥ 平面 PEF. 又 BE ⊂ 平面 ABEF , ∴ 平面 PEF ⊥ 平面 ABEF. (2) 解 : 过点 P 作 PO ⊥ EF 于点 O , 过点 O 作 BE 的平行线交 AB 于点 G , 则 PO ⊥ 平面 ABEF , 以 O 为坐标原点 , 以 OG , OE , OP 所在 直线 分别 为 x 轴、 y 轴、 z 轴建立空间直角 坐 标 系 , 如图所示 . 方法技巧 解决与折叠有关问题的方法 解决与折叠有关的问题的关键是搞清折叠前后的变化量和不变量 , 一般情况下 , 折线同一侧的 , 线段的长度是不变量 , 而位置关系往往会发生变化 , 抓住不变量是解决问题的突破口 . (1) 证明 : 取 AD 的中点 O , 连接 OB , OP , ∵ BA=BD , EA=ED , 即 PA=PD , ∴ OB ⊥ AD 且 OP ⊥ AD , 又 OB ∩ OP=O , ∴ AD ⊥ 平面 BOP , 而 PB ⊂ 平面 BOP , ∴ PB ⊥ AD. (2) 解 : ∵ OP= 1, OB= 2, OP 2 +OB 2 = 5 =PB 2 , ∴ PO ⊥ OB , ∴ OP , OB , OD 两两互相垂直 , 以 O 为坐标原点 , OB , OD , OP 所在的直线为 x , y , z 轴建立如图所示空间直角坐标系 ,