2020高中数学 第一章 计数原理1.3.1 二项式定理导学提纲 2页

‎1.3.1‎‎ 二项式定理导学提纲 班级：___________ 姓名：______________ 小组：_______________‎ ‎【学习目标】‎ 1. 掌握二项式定理及其展开式的通项公式.‎ 2. 会用二项式定理解决与二项展开式有关的简单问题．‎ ‎【重点难点】‎ 重点：掌握二项式定理及其展开式的通项公式.‎ 难点：会用二项式定理解决与二项展开式有关的简单问题．‎ 一、基础感知 知识点一　二项式定理 ‎(a＋b)n＝______________________________(n∈N*)．‎ ‎(1)这个公式所表示的规律叫做二项式定理．‎ ‎(2)展开式：等号右边的多项式叫做(a＋b)n的二项展开式，展开式中一共有__________项．‎ ‎(3)二项式系数：各项的系数C(k∈{0,1,2，…，n})叫做________________．‎ 知识点二　二项展开式的通项公式 ‎(a＋b)n展开式的第__________项叫做二项展开式的通项，记作Tk＋1＝________________.‎ ‎　‎ 二、深入学习 题型一　二项式定理的正用、逆用 例1　利用(a＋b)n的二项展开式解题．‎ ‎(1)求(a＋2b)4的展开式； (2)求(2x－)5的展开式．‎ ‎　‎ ‎　‎ 跟踪训练1　(1)求(3＋)4的展开式；‎ ‎(2)化简(x－1)5＋5(x－1)4＋10(x－1)3＋10(x－1)2＋5(x－1)．‎ ‎　‎ 2‎ 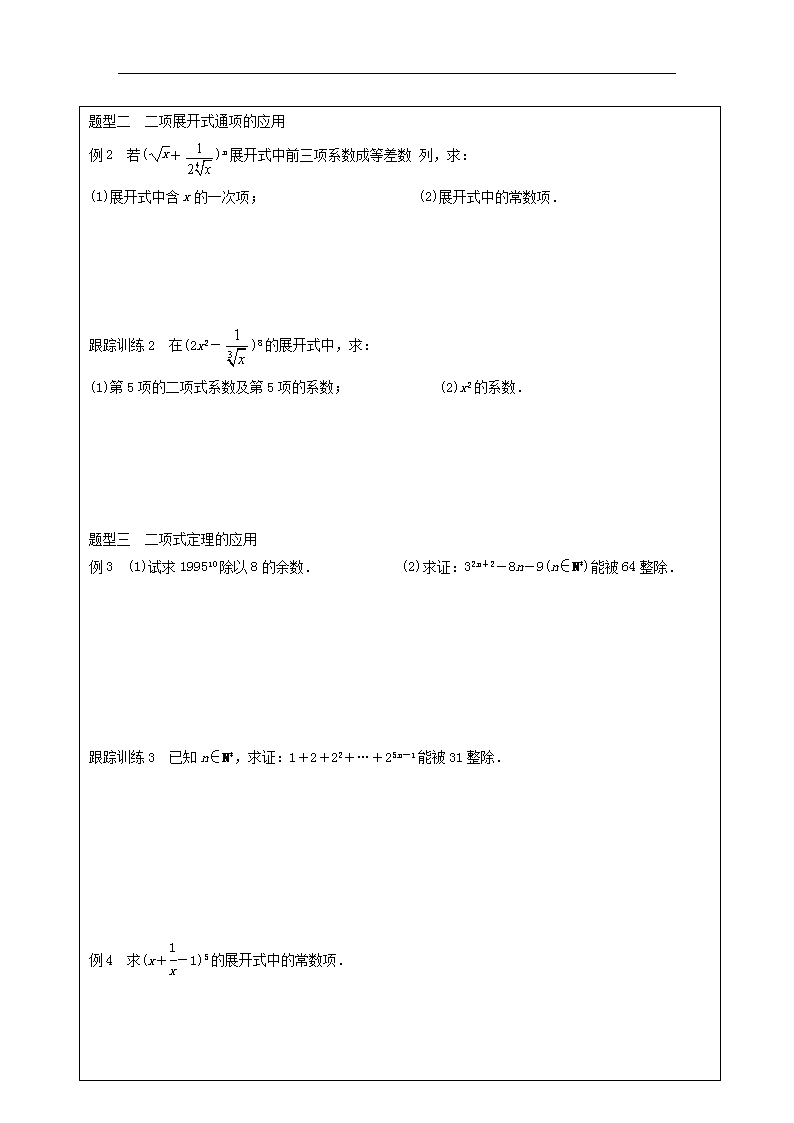题型二　二项展开式通项的应用 例2　若(＋)n展开式中前三项系数成等差数 列，求：‎ ‎(1)展开式中含x的一次项； (2)展开式中的常数项．‎ ‎　‎ 跟踪训练2　在(2x2－)8的展开式中，求：‎ ‎(1)第5项的二项式系数及第5项的系数； (2)x2的系数．‎ 题型三　二项式定理的应用 例3　(1)试求199510除以8的余数． (2)求证：32n＋2－8n－9(n∈N*)能被64整除．‎ ‎　‎ 跟踪训练3　已知n∈N*，求证：1＋2＋22＋…＋25n－1能被31整除．‎ ‎　‎ ‎　‎ 例4　求(x＋－1)5的展开式中的常数项．‎ 2‎