2020届高三数学上学期期中试题 文（新版）人教版 9页

‎2019届高三数学上学期期中试题 文 一、选择题（每小题5分，共60分。每小题所给选项只有一项符合题意，请将正确答案的选项填涂在答题卡上）‎ ‎1．已知复数（为虚数单位），则复数在复平面内对应的点位于（ ）‎ A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限 ‎2．如图，设全集为U=R，A={x|x（x﹣2）＜0}，B={x|y=ln（1﹣x）}，则图中阴影部分表示的集合为（　　）‎ A．{x|x≥1}B．{x|1≤x＜2}C．{x|0＜x≤1} D．{x|x≤1}‎ ‎3．曲线在点处的切线方程是（ ）‎ A. B. C. D. ‎ ‎4．已知平面向量=（0，﹣1），=（1，1），|λ +|=，则λ的值为（　　）‎ A．3 B．2 C．3或﹣1 D．2或﹣1‎ ‎5．若tan（θ+）=﹣3，则=（　　）‎ A．﹣1 B．1 C．﹣2 D．2‎ ‎6．已知等比数列中，，则的值为（   ）‎ A．2 B．4 C．8 D．16‎ ‎7．设是两条不同的直线, 是两个不同的平面, ,则“”是“”的（ ）‎ A. 充分不必要条件 B. 必要不充分条件 C. 充分必要条件 D. 既不充分又不必要条件 ‎8．《九章算术》是我国古代数学成就的杰出代表作，其中《方田》给出计算弧田面积所用的经验公式为：弧田面积=（弦×矢+矢2），弧田（如图）由圆弧和其所对弦所围成，公式中“弦”指圆弧所对弦长，“矢”等于半径长与圆心到弦的距离之差．现有圆心角为，半径等于4米的弧田，按照上述经验公式计算所得弧田面积约是（ ）‎ A. 6平方米 B. 9平方米 ‎ ‎ C. 12平方米 D. 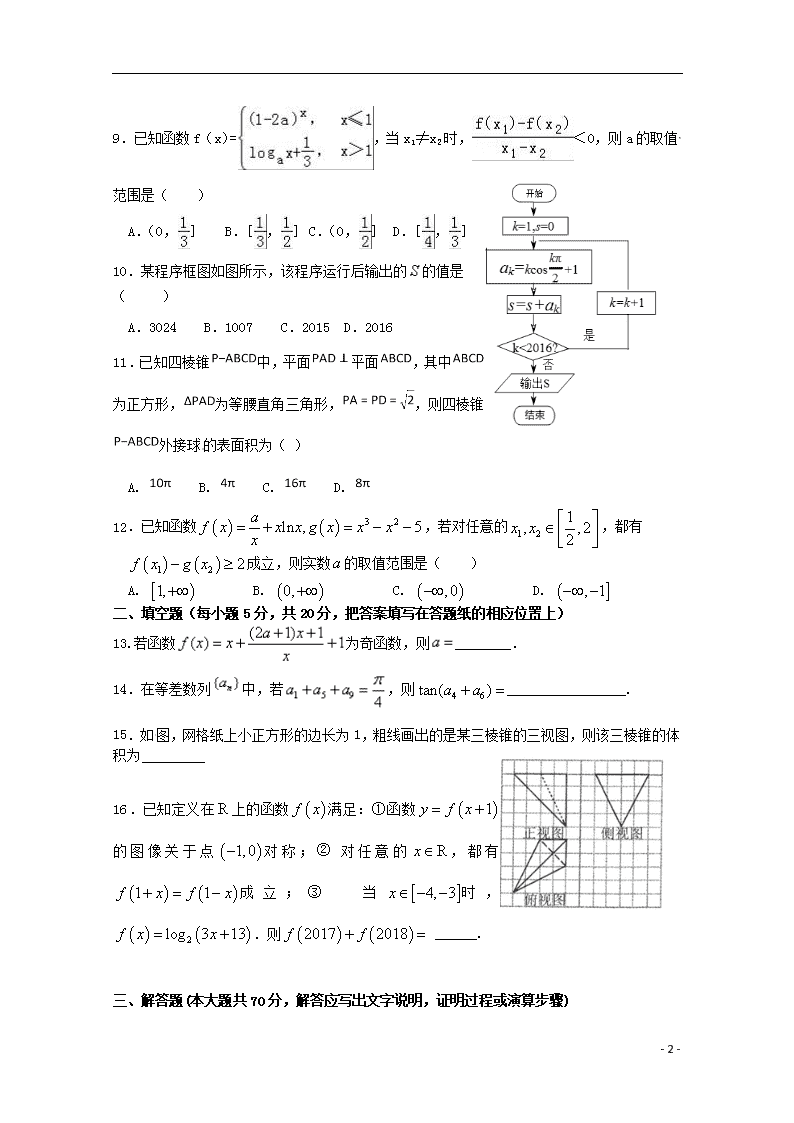15平方米 - 9 -‎ ‎9．已知函数f（x）=，当x1≠x2时，＜0，则a的取值范围是（　　）‎ A．（0，] B．[，] C．（0，] D．[，]‎ ‎10．某程序框图如图所示，该程序运行后输出的的值是（   ）‎ A．3024 B．1007 C．2015 D．2016‎ ‎11．已知四棱锥中，平面平面，其中为正方形，为等腰直角三角形，，则四棱锥外接球的表面积为（ ）‎ A. B. C. D. ‎ ‎12．已知函数，若对任意的，都有成立，则实数的取值范围是（ ）‎ A. B. C. D. 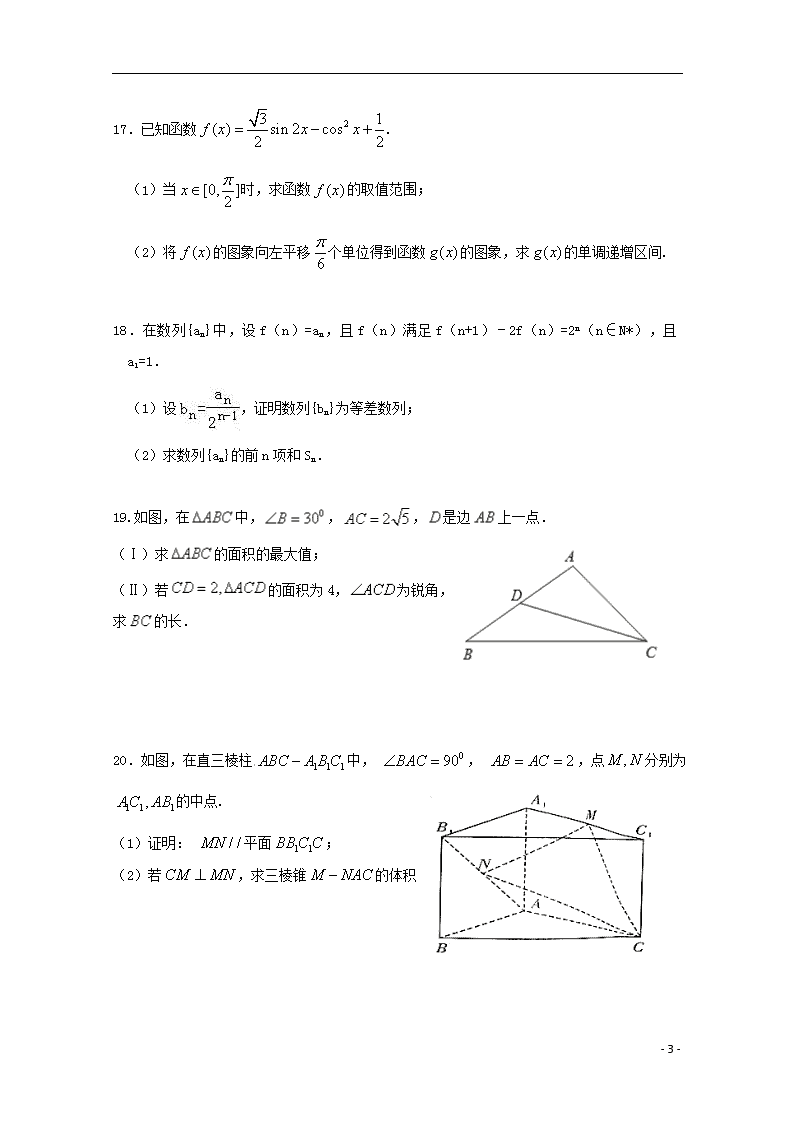‎ 二、填空题（每小题5分，共20分，把答案填写在答题纸的相应位置上）‎ ‎13.若函数为奇函数，则________．‎ ‎14．在等差数列中，若，则_________________.‎ ‎15．如图，网格纸上小正方形的边长为1，粗线画出的是某三棱锥的三视图，则该三棱锥的体积为　　 ‎ ‎16．已知定义在上的函数满足：①函数的图像关于点对称；②对任意的，都有成立；③当时， ．则 ______.‎ 三、解答题(本大题共70分，解答应写出文字说明，证明过程或演算步骤)‎ - 9 -‎ ‎17．已知函数.‎ ‎（1）当时，求函数的取值范围；‎ ‎（2）将的图象向左平移个单位得到函数的图象，求的单调递增区间.‎ ‎18．在数列{an}中，设f（n）=an，且f（n）满足f（n+1）﹣2f（n）=2n（n∈N*），且a1=1．‎ ‎（1）设，证明数列{bn}为等差数列；‎ ‎（2）求数列{an}的前n项和Sn．‎ ‎19.如图，在中，，，是边上一点．‎ ‎（Ⅰ）求的面积的最大值；‎ ‎（Ⅱ）若的面积为4，为锐角，求的长．‎ ‎20．如图，在直三棱柱中， ， ，点分别为的中点.‎ ‎（1）证明： 平面；‎ ‎（2）若，求三棱锥的体积 - 9 -‎ ‎21.已知函数 ‎（Ⅰ）求函数的单调区间；‎ ‎（Ⅱ）若时，关于的不等式恒成立，求整数的最小值．‎ 选做题:二选一（本题满分10分）请用2B铅笔在所选答题号框涂黑 ‎22选修4-4：坐标系与参数方程 在平面直角坐标系中，已知曲线： ，以平面直角坐标系的原点为极点， 轴正半轴为极轴，取相同的单位长度建立极坐标系.已知直线 ： .‎ ‎(Ⅰ)试写出直线的直角坐标方程和曲线的参数方程；‎ ‎(Ⅱ)在曲线上求一点，使点到直线的距离最大，并求出此最大值 ‎23．[选修 4-5]不等式选讲 已知.‎ ‎ (Ⅰ)当，解不等式；‎ ‎ (Ⅱ)对任意， 恒成立，求的取值范围.‎ - 9 -‎ 莆田一中2017-2018学年度上学期第一学段考试试卷 高三 数学文科 参考答案 ‎1-5. DBACD 6-10. BABAA 11-12. DA 13. -1 14. 15. 16. 2‎ ‎17（1）∵ 3分 ‎ ‎∵时，，4分 ∴. 5分 ‎∴函数的取值范围为：. 6分 ‎（2）∵，8分 ‎∴令，，‎ 即可解得的单调递增区间为：，. 12分 ‎18．（1）证明：由已知得，‎ 得，‎ ‎∴bn+1﹣bn=1， 又a1=1，∴b1=1，‎ ‎∴{bn}是首项为1，公差为1的等差数列．‎ ‎（2）解：由（1）知，，∴．‎ ‎∴，‎ 两边乘以2，得，‎ 两式相减得=2n﹣1﹣n•2n=（1﹣n）2n﹣1，‎ ‎∴‎ - 9 -‎ ‎19。因为在 中，是边上一点，所以由余弦定理得：‎ 所以 所以 所以的面积的最大值为 ‎（2）设，在中，‎ 因为的面积为，为锐角，‎ 所以 所以，‎ 由余弦定理得，‎ 所以，‎ 由正弦定理，得，所以，所以，‎ 此时，所以,所以的长为 ‎20试题解析：解：（Ⅰ）证明：连接，，点，分别为， 的中点，所以为△的一条中位线， ‎ 平面， 平面， ‎ 所以平面． ‎ ‎ ‎ - 9 -‎ ‎（Ⅱ）设点，分别为，的中点，，则，，，由，得，解得，又平面，，‎ ‎． ‎ 所以三棱锥的体积为.‎ ‎21（Ⅰ）‎ ‎……（1分）‎ 当时，由，得，由，得 所以的单调递增区间为，单调递减区间为； ……（3分）‎ 当时，由，得，由，得，所以的单调递增区间为，单调递减区间为 ……（5分）‎ ‎（Ⅱ）令 ‎……（6分）‎ 当时，，所以函数在上单调递增，‎ 而，所以关于的不等式 不恒成立； ……（8分）‎ 当时，若，；若，‎ - 9 -‎ 所以函数在上单调递增，在上单调递减，所以…（10分）‎ 令，因为，‎ 又在上是减函数，所以当时，，故整数的最小值为1． ……（12分）‎ ‎22由题意知，直线的直角坐标方程为： ，∴曲线的参数方程为（为参数）‎ ‎（2）设点的坐标，则点到直线的距离为 ‎，‎ ‎∴当时，点，此时 ‎23（1）依题意，得 则不等式，即为 或或解得.‎ 故原不等式的解集为.‎ ‎（2）由题得， ，‎ - 9 -‎ 当且仅当，‎ 即时取等号，‎ ‎∴，‎ ‎∴，‎ ‎∵，∴， ，‎ ‎∴，‎ ‎∴.‎ - 9 -‎