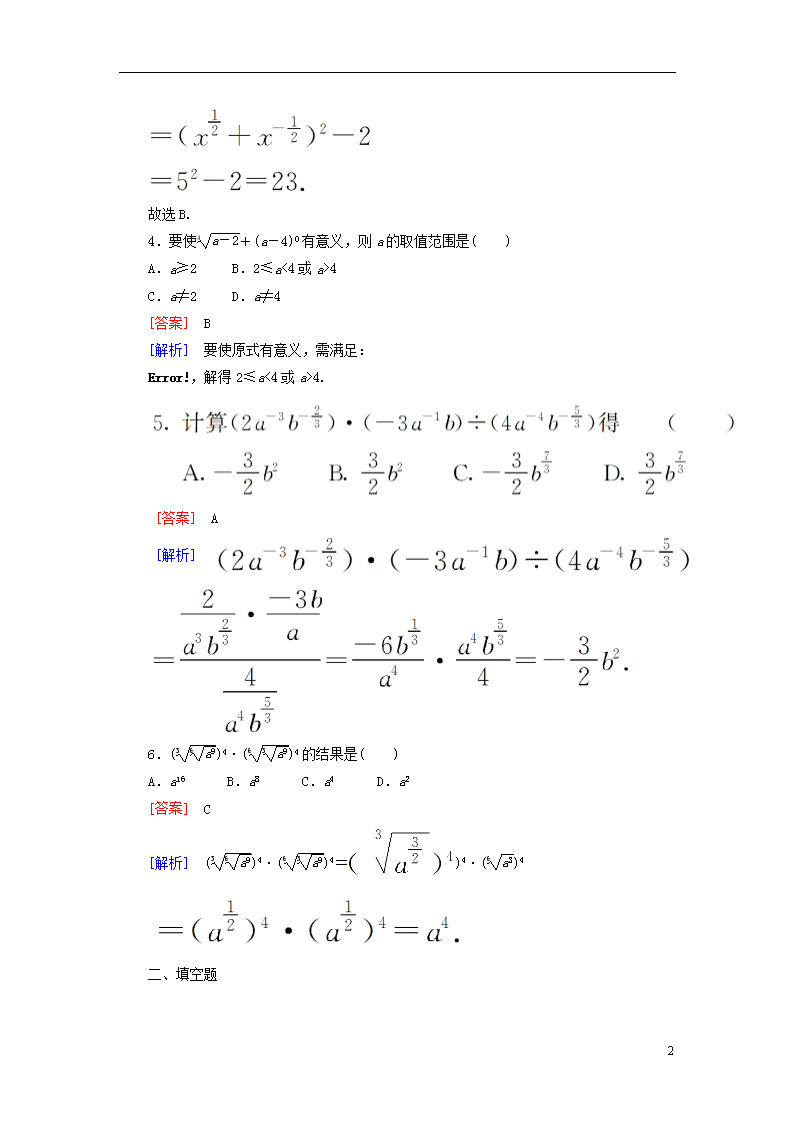2020高中数学第三章指数函数和对数函数3 7页

指数扩充及其运算性质 基 础 巩 固 一、选择题 ‎1．若有意义，则x的取值范围是(　　)‎ A．x∈R B．x≠ C．x> D．x< ‎[答案]　D ‎[解析]　 ＝，要使有意义，则需1－2x>0，即x<.‎ ‎2．以下化简结果错误的是(　　)‎ ‎[答案]　D ‎[解析]　 ‎ 故选项D错误．‎ A．5　　　B．‎23　‎　　C．25　　　D．27‎ ‎[答案]　B ‎[解析]　＝x＋＝x＋x－1‎ 7‎ 故选B.‎ ‎4．要使＋(a－4)0有意义，则a的取值范围是(　　)‎ A．a≥2 B．2≤a<4或a>4‎ C．a≠2 D．a≠4‎ ‎[答案]　B ‎[解析]　要使原式有意义，需满足：‎ ，解得2≤a<4或a>4.‎ ‎ [答案]　A ‎ [解析]　 ‎ ‎6．()4·()4的结果是(　　)‎ A．a16　　　B．a‎8　‎　　C．a4　　　D．a2‎ ‎[答案]　C ‎[解析]　()4·()4＝)4·()4‎ 二、填空题 7‎ ‎7．(2012·临淄高一检测)0.25×(－)－4－4÷20－＝________.‎ ‎[分析]　本小题考查分数指数幂的运算，利用运算性质，运用法则即可求解．‎ ‎[答案]　－4‎ ‎[解析]　 ‎ ‎＝×()－4－4－‎ ‎＝4－4－4＝－4.‎ ‎8．(2012·郑州模拟)设函数f1(x)＝x，f2(x)＝x－1，f3(x)＝x2，则f1(f2(f3(2012)))＝________.‎ ‎[答案]　 ‎[解析]　f1(f2(f3(2012)))＝f1(f2(20122))＝f1((20122)－1)＝((20122)－1)＝2012－1＝.‎ 三、解答题 ‎9．(1)已知＋b＝1，求的值．‎ ‎ [解析]　(1)＝＝‎32a＋b÷3 ‎∵a＋b＝1，∴＝3.‎ 7‎ ‎ ‎ 能 力 提 升 一、选择题 ‎ [答案]　A ‎[解析]　 利用平方差公式易求选A.‎ ‎2．下列结论中正确的个数是(　　)‎ A．0 B．1‎ C．2 D．3‎ ‎[答案]　B ‎[解析]　取a＝－2，可验证①不正确；‎ 当a<0，n为奇数时，②不正确；‎ y＝(x－2) －(3x－7)0的定义域应是[2，)∪(，＋∞)，③不正确；‎ ‎④由‎100a＝5得‎102a＝5.(1)‎ 又10b＝2.(2)‎ ‎(1)×(2)得‎102a＋b＝10.‎ 7‎ ‎∴‎2a＋b＝1，此命题正确．‎ 二、填空题 ‎3．若有意义，则－|3－x|化简后的结果是________．‎ ‎[答案]　－1‎ ‎[解析]　∵有意义，∴2－x≥0.‎ ‎∴x≤2.‎ ‎∴－|3－x|‎ ‎＝|x－2|－|3－x|＝(2－x)－(3－x)＝－1.‎ ‎[答案]　－23‎ ‎[解析]　 ‎ 三、解答题 ‎5．化简下列各式：‎ ‎ (2)(a＞b，b＞0)．‎ ‎[分析]　在指数式运算中，一定要注意运算顺序和灵活运用乘法公式．‎ ‎[解析]　 ‎ 7‎ ‎ [点评]　这种混合运算的题型，运算的关键是化简顺序：先乘方、再乘除，最后做加减，步步紧扣运算法则，同时应注意将系数和字母分开计算．‎ ‎6．已知a＝－，b＝，求的值．‎ ‎[解析]　∵a≠0，‎ ‎7．已知a、b是方程x2－6x＋4＝0的两根，且a>b>0，求的值．‎ ‎[解析]　∵a、b是方程x2－6x＋4＝0的两根，‎ ‎∴.‎ ‎()2＝＝＝，‎ 7‎ ‎∵a>b>0，∴>，‎ ‎∴＝＝. ‎ 7‎