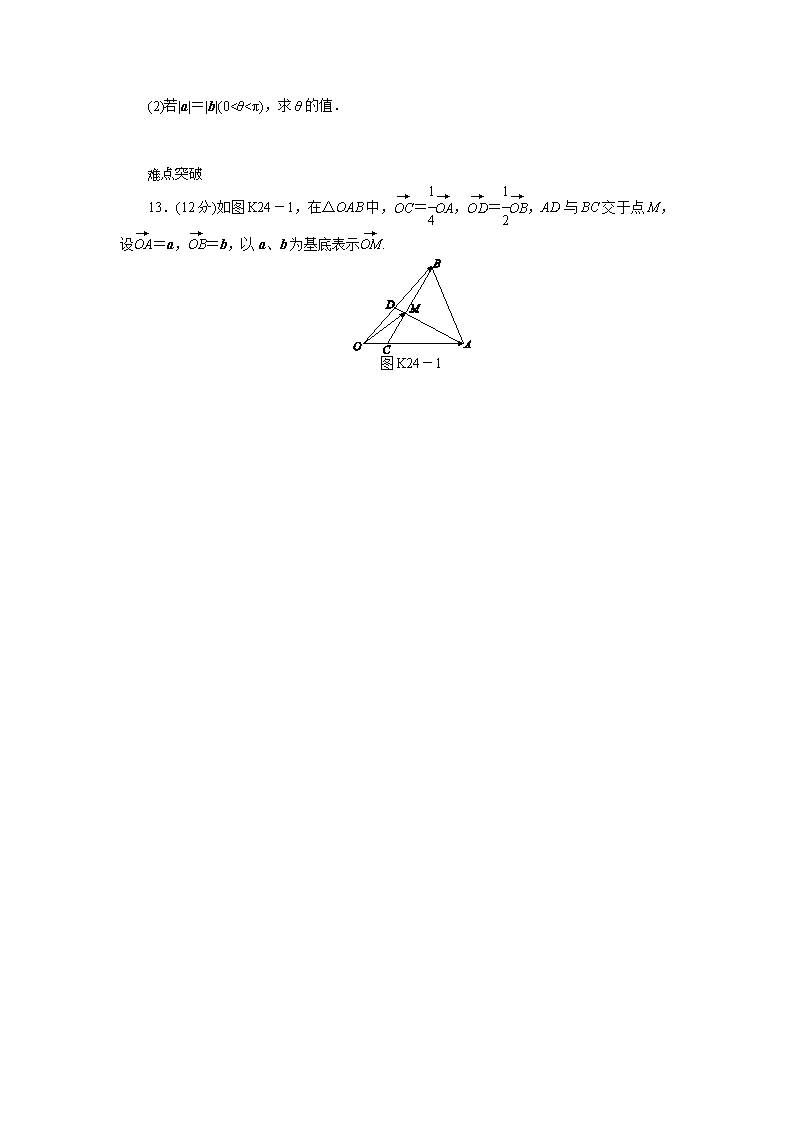2013届人教A版文科数学课时试题及解析（24）平面向量基本定理及向量坐标运算 4页

课时作业(二十四)　[第24讲　平面向量基本定理及向量坐标运算]‎ ‎ [时间：35分钟　　分值：80分]‎ ‎　 ‎1．已知点A(－1，－5)和向量a＝(2,3)，若＝‎3a，则点B的坐标为(　　)‎ A．(6,9) B．(5,4) C．(7,14) D．(9,24)‎ ‎2．原点O在正六边形ABCDEF的中心，＝(－1，－)，＝(1，－)，则等于(　　)‎ A．(2,0) B．(－2,0)‎ C．(0，－2) D．(0，)‎ ‎3．已知向量a，b不共线，且＝a＋4b，＝－a＋9b，＝‎3a－b，则一定共线的是(　　)‎ A．A，B，D B．A，B，C C．B，C，D D．A，C，D ‎4．已知向量a＝(2,3)，b＝(－1,2)，若ma＋nb与a－2b共线，则＝________.‎ ‎5． 已知向量a＝(1,2)，b＝(1,0)，c＝(3,4)．若λ为实数，(a＋λb)∥c，则λ＝(　　)‎ A. B. C．1 D．2‎ ‎6． a，b是不共线的向量，若＝k‎1a＋b，＝a＋k2b(k1、k2∈R)，则A，B，C三点共线的充要条件是(　　)‎ A．k1＝k2＝1 B．k1＝k2＝－1‎ C．k1k2＝1 D．k1k2＝－1‎ ‎7．已知O、A、B是平面上的三个点，直线AB上有一点C，满足2＋＝0，则＝(　　)‎ A．2－ B．－＋2 C.－ D．－＋ ‎8．已知平面向量a＝(1，－1)，b＝(－1,2)，c＝(3，－5)，则用a，b表示向量c为(　　)‎ A．‎2a－b B．－a＋2b C．a－2b D．a＋2b ‎9．已知＝(2，－1)，＝(－4,1)，则的坐标为________．‎ ‎10． 设向量a，b满足|a|＝2，b＝(2,1)，且a与b的方向相反，则a的坐标为________．‎ ‎11． 已知坐标平面内定点A(－1,0)，B(1,0)，M(4,0)，N(0,4)和动点P(x1，y1)，Q(x2，y2)．若·＝3，＝＋，其中O为坐标原点，则||的最小值是________．‎ ‎12．(13分)已知向量a＝(sinθ，cosθ－2sinθ)，b＝(1,2)．‎ ‎(1)若a∥b，求tanθ的值；‎ ‎(2)若|a|＝|b|(0<θ<π)，求θ的值．‎ ‎13．(12分)如图K24－1，在△OAB中，＝，＝，AD与BC交于点M，设＝a，＝b，以a、b为基底表示.‎ 图K24－1‎ 课时作业(二十四)‎ ‎【基础热身】‎ ‎1．B　[解析] ＝(－1，－5)，＝‎3a＝(6,9)，故＝＋＝(5,4)，故点B坐标为(5,4)．‎ ‎2．A　[解析] ∵正六边形中，OABC为平行四边形，‎ ‎∴＝＋，‎ ‎∴＝－＝(2,0)．‎ ‎3．A　[解析] ＝＋＝－a＋9b＋‎3a－b ‎＝‎2a＋8b.‎ ‎∵＝a＋4b，∴＝，∴A、B、D三点共线．‎ ‎4．－　[解析] ma＋nb＝(‎2m,‎3m)＋(－n,2n)＝(‎2m－n,‎3m＋2n)，‎ a－2b＝(2,3)－(－2,4)＝(4，－1)．‎ 由于ma＋nb与a－2b共线，则有＝，‎ ‎∴n－‎2m＝‎12m＋8n，∴＝－.‎ ‎【能力提升】‎ ‎5．B　[解析] 因为a＋λb＝(1,2)＋λ(1,0)＝(1＋λ，2)，又因为(a＋λb)∥c，‎ 所以(1＋λ)×4－2×3＝0，解得λ＝.‎ ‎6．C　[解析] A，B，C三点共线等价于＝λ，‎ ‎∴k‎1a＋b＝λ(a＋k2b)，∴k1＝λ，1＝λk2，‎ ‎∴k1k2＝1.‎ ‎7．A　[解析] ∵2＋＝0，‎ ‎∴2(－)＋(－)＝0，‎ ‎∴＋－2＝0，∴＝2－.‎ ‎8．C　[解析] 设c＝xa＋yb，∴(3，－5)＝(x－y，－x＋2y)，‎ ‎∴解得 ‎∴c＝a－2b.‎ ‎9．(－6,2)　[解析] 　＝－＝(－6,2)．‎ ‎10．(－4，－2)　[解析] 因为a与b的方向相反，根据共线向量定义有：a＝λb(λ<0)，所以a＝(2λ，λ)．‎ 由＝2，得＝2⇒λ＝－2或λ＝2(舍去)，故a＝(－4，－2)．‎ ‎11．2－2　[解析] 由已知得P的坐标满足(x1＋1，y1)·(x1－1，y1)＝3，即x＋y＝4.‎ 动点Q的坐标满足(x2，y2)＝(4,0)＋(0,4)，‎ 故x2＝2－4t，y2＝2＋4t，即x2＋y2＝4.‎ ‎||的最小值即圆x2＋y2＝4上的点到直线x＋y＝4上的点的最小距离，最小距离为2－2，故||的最小值是2－2.‎ ‎12．[解答] (1)因为a∥b，所以2sinθ＝cosθ－2sinθ，‎ 于是4sinθ＝cosθ，故tanθ＝.‎ ‎(2)由|a|＝|b|知，sin2θ＋(cosθ－2sinθ)2＝5，‎ 所以1－2sin2θ＋4sin2θ＝5，‎ 从而－2sin2θ＋2(1－cos2θ)＝4，即sin2θ＋cos2θ＝－1，‎ 于是sin＝－.‎ 又由0<θ<π知，<2θ＋<，‎ 所以2θ＋＝，或2θ＋＝.‎ 因此θ＝或θ＝.‎ ‎【难点突破】‎ ‎13．[解答] 设＝ma＋nb(m，n∈R)，‎ 则＝－＝(m－1)a＋nb，‎ ＝－＝b－a.‎ 因为A、M、D三点共线，所以＝，即m＋2n＝1，‎ 又＝－＝a＋nb，‎ ＝－＝－a＋b，‎ 因为C、M、B三点共线，所以＝，‎ 即‎4m＋n＝1，‎ 由解得 ‎∴＝a＋b.‎ ‎ ‎