高中数学立体几何常考证明题汇总 6页

新课标立体几何常考证明题汇总 1、已知四边形 ABCD是空间四边形， , , ,E F G H 分别是边 , , ,AB BC CD DA的中点 （1） 求证：EFGH 是平行四边形 （2） 若 BD= 23，AC=2，EG=2。求异面直线 AC、BD 所成的角和 EG、BD 所成的角。 证明：在 ABD 中，∵ ,EH分别是 ,AB AD 的中点∴ 1// , 2EH BD EH BD 同理， 1// , 2FG BD FG BD ∴ // ,EH FG EH FG ∴四边形 EFGH 是平行四边形。 (2) 90° 30 ° 考点：证平行（利用三角形中位线），异面直线所成的角 2、如图，已知空间四边形 ABCD中， ,BC AC AD BD， E 是 AB 的中点。 求证：（1） AB 平面 CDE; （2）平面CDE  平面 ABC 。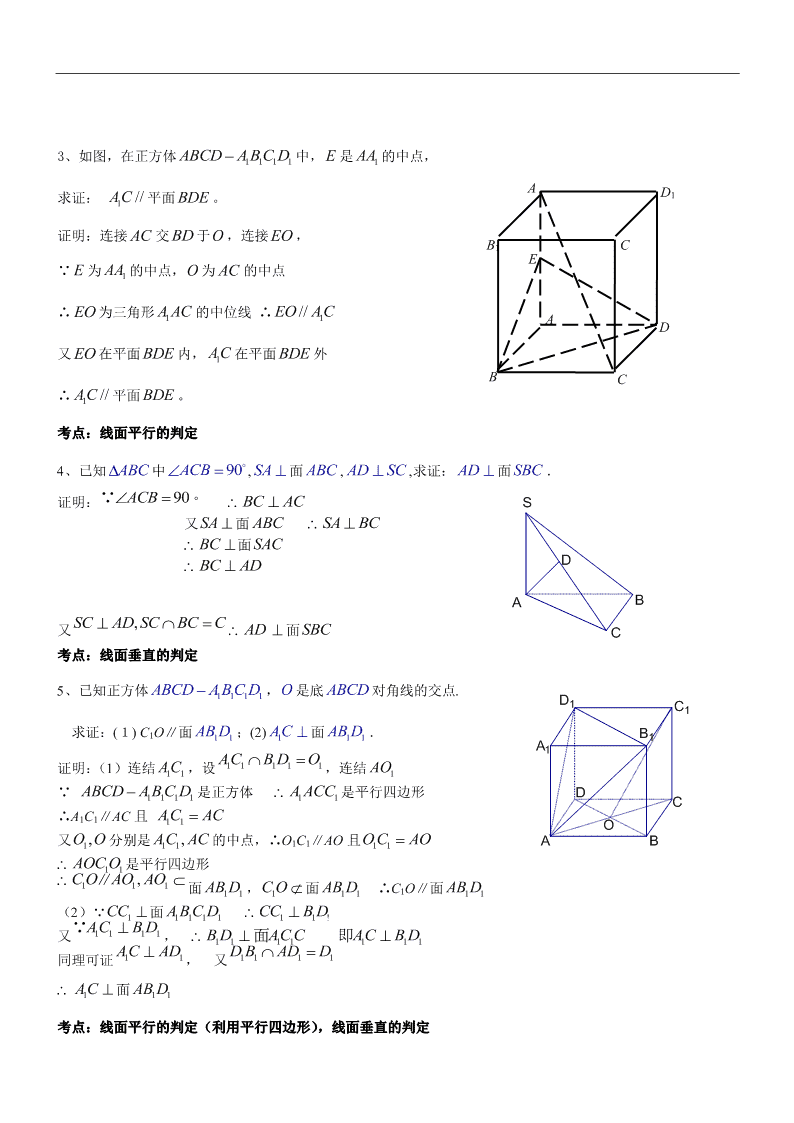 证明：（1） BC AC CE ABAE BE     同理， AD BD DE ABAE BE     又∵CE DE E ∴ AB 平面CDE （2）由（1）有 平面 又∵ AB  平面 ABC ， ∴平面 平面 ABC 考点：线面垂直，面面垂直的判定 A H G F E D C B A E D B C 3、如图，在正方体 1 1 1 1ABCD A B C D 中， E 是 1AA 的中点， 求证： 1 //AC 平面 BDE 。 证明：连接 AC 交 BD 于O ，连接 EO ， ∵ 为 的中点， 为 的中点 ∴ 为三角形 1A AC 的中位线 ∴ 1//EO AC 又 在平面 内， 1AC在平面 外 ∴ 平面 。 考点：线面平行的判定 4、已知 ABC 中 90ACB, SA  面 ABC , AD SC ,求证： AD  面 SBC ． 证明： 90ACB∵ ° BC AC 又 SA  面 ABC SA BC BC面 SAC BC AD 又 ,SC AD SC BC C   AD  面 SBC 考点：线面垂直的判定 5、已知正方体 1 1 1 1ABCD A BC D ，O 是底 ABCD对角线的交点. 求证：(１) C1O∥面 11AB D ；(2) 1AC  面 11AB D ． 证明：（1）连结 11AC ，设 1 1 1 1 1AC B D O，连结 1AO ∵ 1 1 1 1ABCD A B C D 是正方体 11A ACC 是平行四边形 ∴A1C1∥AC 且 11AC AC 又 1,OO分别是 11,AC AC 的中点，∴O1C1∥AO 且 11O C AO 11AOC O 是平行四边形 1 1 1,C O AO AO∥ 面 11AB D ， 1CO 面 ∴C1O∥面 11AB D （2） 1CC  面 1 1 1 1A B C D 1 1 !CC B D 又 1 1 1 1AC B D∵ ， 1 1 1 1B D AC C面 1 1 1AC B D即 同理可证 11AC AD ， 又 1 1 1 1D B AD D  1AC  面 11AB D 考点：线面平行的判定（利用平行四边形），线面垂直的判定 A 1 E D1 C 1 B1 D C B A S D C BA D1 O D BA C1 B1A1 C N M P C B A 6、正方体 ABCD A B C D 中，求证：（1） 'AC B D DB 平面 ；（ 2） 'BD ACB 平面 . 考点：线面垂直的判定 7、正方体 ABCD—A1B1C1D1 中．(1)求证：平面 A1BD∥平面 B1D1C； (2)若 E、F 分别是 AA1，CC1 的中点，求证：平面 EB1D1∥平面 FBD． 证明：(1)由 B1B∥DD1，得四边形 BB1D1D 是平行四边形，∴B1D1∥BD， 又 BD 平面 B1D1C，B1D1  平面 B1D1C， ∴BD∥平面 B1D1C． 同理 A1D∥平面 B1D1C． 而 A1D∩BD＝D，∴平面 A1BD∥平面 B1CD． (2)由 BD∥B1D1，得 BD∥平面 EB1D1．取 BB1 中点 G，∴AE∥B1G． 从而得 B1E∥AG，同理 GF∥AD．∴AG∥DF．∴ B1E∥DF．∴DF∥平面 EB1D1．∴平面 EB1D1∥平面 FBD． 考点：线面平行的判定（利用平行四边形） 8、四面体 ABCD中， ,,AC BD E F 分别为 ,AD BC 的中点，且 2 2EF AC ， 90BDC，求证： BD 平面 ACD 证明：取CD 的中点G ，连结 ,EG FG ，∵ ,EF分别为 的中点，∴ EG 1 2 // AC 1 2 //FG BD ，又 ,AC BD ∴ 1 2FG AC ，∴在 EFG 中， 2 2 2 21 2EG FG AC EF   ∴ EG FG ，∴ BD AC ，又 ，即 BD CD ， AC CD C ∴ 平面 考点：线面垂直的判定,三角形中位线，构造直角三角形 9、如图 P 是 ABC 所在平面外一点， ,PA PB CB平面 PAB ，M 是 PC 的中点，N 是 AB 上的点， 3AN NB （1）求证： MN AB ；（ 2）当 90APB， 24AB BC时，求 MN 的长。 A1 A B1 B C1 C D1 D G E F 证明：（1）取 PA 的中点Q ，连结 ,MQ NQ ，∵ M 是 PB 的中点， ∴ //MQ BC ，∵ CB  平面 PAB ，∴ MQ  平面 ∴QN 是 MN 在平面 内的射影 ，取 AB 的中点 D ，连结 PD ，∵ ,PA PB ∴ PD AB ，又 3AN NB ， ∴ BN ND [来源:学§科§网] ∴ //QN PD ，∴QN AB ，由三垂线定理得 MN AB （2）∵ 90APB， ∴ 1 22PD AB，∴ 1QN  ，∵ 平面 .∴ MQ NQ ，且 1 12MQ BC，∴ 2MN  考点：三垂线定理 10、如图，在正方体 1 1 1 1ABCD A B C D 中， E 、 F 、G 分别是 AB 、 AD 、 11CD的中点.求证：平面 1D EF ∥ 平面 BDG . 证明：∵ 、 分别是 、 的中点， EF ∥ BD 又 EF 平面 ， BD  平面 ∥平面 ∵ 1DG EB 四边形 1D GBE 为平行四边形， 1DE∥GB 又 1DE 平面 ，GB  平面 1DE∥平面 1EF D E E， 平面 ∥平面 考点：线面平行的判定（利用三角形中位线） 11、如图，在正方体 中， 是 1AA 的中点. （1）求证： 1 //AC 平面 BDE ； （2）求证：平面 1A AC  平面 . 证明：（1）设 AC BD O， ∵ 、O 分别是 1AA 、 AC 的中点， 1AC∥ EO 又 1AC 平面 BDE ， EO  平面 ， ∥平面 （2）∵ 1AA  平面 ABCD， BD  平面 ， 1AA BD 又 BD AC ， 1AC AA A， BD  平面 1A AC ， BD  平面 ， 平面 BDE  平面 考点：线面平行的判定（利用三角形中位线），面面垂直的判定 12、已知 ABCD是矩形，PA 平面 ABCD， 2AB  ， 4PA AD，E 为 BC 的中点． （1）求证： DE 平面 PAE ；（ 2）求直线 DP 与平面 所成的角． 证明：在 ADE 中， 2 2 2AD AE DE， AE DE ∵ 平面 ， DE  平面 ， PA DE 又 PA AE A， 平面 （2） DPE 为 DP 与平面 PAE 所成的角 在 Rt PAD ， 42PD  ，在 Rt DCE 中， 22DE  在 Rt DEP 中， 2PD DE ， 030DPE 考点：线面垂直的判定,构造直角三角形 13、如图，在四棱锥 P ABCD 中，底面 ABCD是 060DAB且边长为 a 的菱形，侧面 PAD 是等边三角形， 且平面 PAD 垂直于底面 ． （1）若G 为 AD 的中点，求证： BG 平面 PAD ； （2）求证： AD PB ； （3）求二面角 A BC P的大小． 证明：（1） ABD 为等边三角形且 为 的中点， BG AD 又平面  平面 ， 平面 （2） 是等边三角形且 为 的中点， AD PG 且 AD BG ， PG BG G， AD  平面 PBG ， PB 平面 ， （3）由 ， AD ∥ BC ， BC PB 又 ， ∥ ， BG BC PBG 为二面角 的平面角 在 Rt PBG 中， PG BG ， 045PBG 考点：线面垂直的判定,构造直角三角形,面面垂直的性质定理，二面角的求法（定义法） 14、如图 1,在正方体 1 1 1 1ABCD A B C D 中， M 为 1CC 的中点，AC 交 BD 于点 O，求证： 1AO 平面 MBD． 证明：连结 MO， 1AM ，∵DB⊥ 1AA，DB⊥AC， 1A A AC A， ∴DB⊥平面 11A ACC ，而 1AO 平面 ∴DB⊥ 1AO． 设正方体棱长为 a ，则 22 1 3 2AO a ， 223 4MO a ． 在 Rt△ 11AC M 中， 22 1 9 4A M a ．∵ 2 2 2 11AO MO A M ，∴ 1AO OM ． ∵OM∩DB=O，∴ 1AO⊥平面 MBD． 考点：线面垂直的判定，运用勾股定理寻求线线垂直 15、如图２，在三棱锥Ａ－BCD 中，BC＝AC，AD＝BD， 作 BE⊥CD，Ｅ为垂足，作 AH⊥BE 于Ｈ．求证：AH⊥平面 BCD． 证明：取 AB 的中点Ｆ，连结 CF，DF． ∵ AC BC ，∴CF AB ． ∵ AD BD ，∴ DF AB ． 又CF DF F ，∴ AB 平面 CDF． ∵CD  平面 CDF，∴CD AB ． 又CD BE ， BE AB B， ∴CD  平面 ABE，CD AH ． ∵ AH CD ， AH BE ，CD BE E， ∴ AH  平面 BCD． 考点：线面垂直的判定 16、证明：在正方体 ABCD－A1B1C1D1 中，A1C⊥平面 BC1D D1 C1 A1 B1 D C A B 证明：连结 AC BD AC∵ ⊥ ∴ AC 为 A1C 在平面 AC 上的射影         BD A C A C BC A C BC D1 1 1 1 1同理可证 平面 考点：线面垂直的判定，三垂线定理 17、如图，过 S 引三条长度相等但不共面的线段 SA、SB、SC，且∠ASB=∠ASC=60°，∠BSC=90°，求证： 平面 ABC⊥平面 BSC． 证明∵SB=SA=SC，∠ASB=∠ASC=60°∴AB=SA=AC 取 BC 的中点 O，连 AO、SO， 则 AO⊥BC，SO⊥BC， ∴∠AOS 为二面角的平面角，设 SA=SB=SC=a，又∠BSC=90°，∴BC= 2 a，SO= 2 2 a， AO2=AC2－OC2=a2－ 2 1 a2= a2，∴SA2=AO2+OS2，∴∠AOS=90°，从而平面 ABC⊥ 平面 BSC． 考点：面面垂直的判定（证二面角是直二面角）