2015年天津市高考数学试卷（文科） 23页

‎2015年天津市高考数学试卷（文科）‎ ‎　‎ 一、选择题：每题5分，在每小题给出的四个选项中，只有一项是符合题目要求的．‎ ‎1．（5分）已知全集U={1，2，3，4，5，6}，集合A={2，3，5}，集合B={1，3，4，6}，则集合A∩∁UB=（　　）‎ A．{3} B．{2，5} C．{1，4，6} D．{2，3，5}‎ ‎2．（5分）若实数x，y满足条件，则z=3x+y的最大值为（　　）‎ A．7 B．8 C．9 D．14‎ ‎3．（5分）阅读如图所示的程序框图，运行相应的程序，则输出i的值为（　　）‎ A．2 B．3 C．4 D．5‎ ‎4．（5分）设x∈R，则“1＜x＜2”是“|x﹣2|＜1”的（　　）‎ A．充分而不必要条件 B．必要而不充分条件 C．充要条件 D．既不充分也不必要条件 ‎5．（5分）已知双曲线﹣=1（a＞0，b＞0）的一个焦点为F（2，0），且双曲线的渐近线与圆（x﹣2）2+y2=3相切，则双曲线的方程为（　　）‎ A．﹣=1 B．﹣=1 C．﹣y2=1 D．x2﹣=1‎ ‎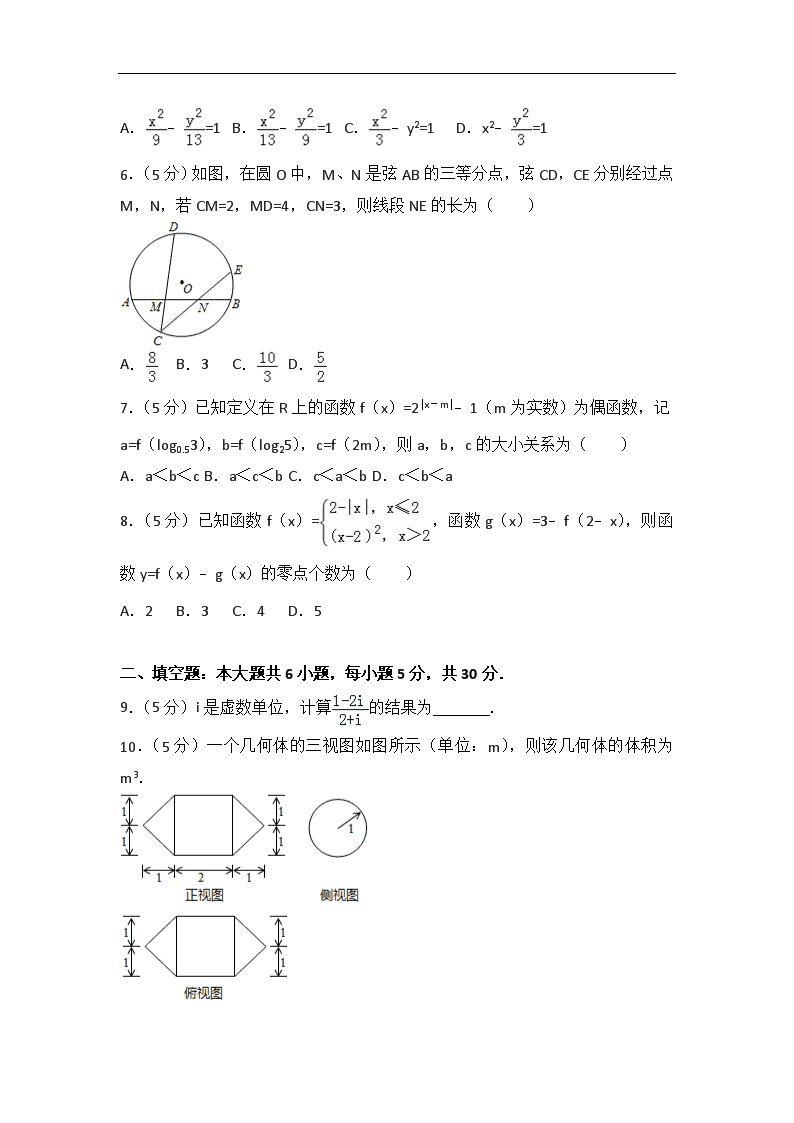6．（5分）如图，在圆O中，M、N是弦AB的三等分点，弦CD，CE分别经过点M，N，若CM=2，MD=4，CN=3，则线段NE的长为（　　）‎ A． B．3 C． D．‎ ‎7．（5分）已知定义在R上的函数f（x）=2|x﹣m|﹣1（m为实数）为偶函数，记a=f（log0.53），b=f（log25），c=f（2m），则a，b，c的大小关系为（　　）‎ A．a＜b＜c B．a＜c＜b C．c＜a＜b D．c＜b＜a ‎8．（5分）已知函数f（x）=，函数g（x）=3﹣f（2﹣x），则函数y=f（x）﹣g（x）的零点个数为（　　）‎ A．2 B．3 C．4 D．5‎ ‎　‎ 二、填空题：本大题共6小题，每小题5分，共30分．‎ ‎9．（5分）i是虚数单位，计算的结果为　 　．‎ ‎10．（5分）一个几何体的三视图如图所示（单位：m），则该几何体的体积为　 　m3．‎ ‎11．（5分）已知函数f（x）=axlnx，x∈（0，+∞），其中a为实数，f′（x）为f（x）的导函数，若f′（1）=3，则a的值为　 　．‎ ‎12．（5分）已知a＞0，b＞0，ab=8，则当a的值为　 　时，log2a•log2（2b）取得最大值．‎ ‎13．（5分）在等腰梯形ABCD中，已知AB∥DC，AB=2，BC=1，∠ABC=60°，点E和F分别在线段BC和DC上，且=，=，则•的值为　 　．‎ ‎14．（5分）已知函数f（x）=sinωx+cosωx（ω＞0），x∈R，若函数f（x）在区间（﹣ω，ω）内单调递增，且函数y=f（x）的图象关于直线x=ω对称，则ω的值为　 　．‎ ‎　‎ 三、解答题：本大题共6小题，共80分，解答应写出文字说明，证明过程或演算步骤．‎ ‎15．（13分）设甲、乙、丙三个乒乓球协会的运动员人数分别为27，9，18，先采用分层抽取的方法从这三个协会中抽取6名运动员组队参加比赛．‎ ‎（Ⅰ）求应从这三个协会中分别抽取的运动员的人数；‎ ‎（Ⅱ）将抽取的6名运动员进行编号，编号分别为A1，A2，A3，A4，A5，A6，现从这6名运动员中随机抽取2人参加双打比赛．‎ ‎（i）用所给编号列出所有可能的结果；‎ ‎（ii）设A为事件“编号为A5和A6的两名运动员中至少有1人被抽到”，求事件A发生的概率．‎ ‎16．（13分）在△ABC中，内角A，B，C所对的边分别为a，b，c，已知△ABC的面积为3，b﹣c=2，cosA=﹣．‎ ‎（Ⅰ）求a和sinC的值；‎ ‎（Ⅱ）求cos（2A+）的值．‎ ‎17．（13分）如图，已知AA1⊥平面ABC，BB1∥AA1，AB=AC=3，BC=2，AA1=，BB1=2，点E和F分别为BC和A1C的中点．‎ ‎（Ⅰ）求证：EF∥平面A1B1BA；‎ ‎（Ⅱ）求证：平面AEA1⊥平面BCB1；‎ ‎（Ⅲ）求直线A1B1与平面BCB1所成角的大小．‎ ‎18．（13分）已知{an}是各项均为正数的等比数列，{bn}是等差数列，且a1=b1=1，b2+b3=2a3，a5﹣3b2=7．‎ ‎（Ⅰ）求{an}和{bn}的通项公式；‎ ‎（Ⅱ）设cn=anbn，n∈N*，求数列{cn}的前n项和．‎ ‎19．（14分）已知椭圆+=1（a＞b＞0）的上顶点为B，左焦点为F，离心率为．‎ ‎（Ⅰ）求直线BF的斜率．‎ ‎（Ⅱ）设直线BF与椭圆交于点P（P异于点B），过点B且垂直于BP的直线与椭圆交于点Q（Q异于点B），直线PQ与y轴交于点M，|PM|=λ|MQ|．‎ ‎（i）求λ的值．‎ ‎（ii）若|PM|sin∠BQP=，求椭圆的方程．‎ ‎20．（14分）已知函数f（x）=4x﹣x4，x∈R．‎ ‎（Ⅰ）求f（x）的单调区间；‎ ‎（Ⅱ）设曲线y=f（x）与x轴正半轴的交点为P，曲线在点P处的切线方程为y=g（x），求证：对于任意的实数x，都有f（x）≤g（x）；‎ ‎（Ⅲ）若方程f（x）=a（a为实数）有两个实数根x1，x2，且x1＜x2，求证：x2﹣x1≤﹣+4．‎ ‎　‎ ‎2015年天津市高考数学试卷（文科）‎ 参考答案与试题解析 ‎　‎ 一、选择题：每题5分，在每小题给出的四个选项中，只有一项是符合题目要求的．‎ ‎1．（5分）已知全集U={1，2，3，4，5，6}，集合A={2，3，5}，集合B={1，3，4，6}，则集合A∩∁UB=（　　）‎ A．{3} B．{2，5} C．{1，4，6} D．{2，3，5}‎ ‎【分析】求出集合B的补集，然后求解交集即可．‎ ‎【解答】解：全集U={1，2，3，4，5，6}，集合B={1，3，4，6}，∁UB={2，5}，又集合A={2，3，5}，‎ 则集合A∩∁UB={2，5}．‎ 故选：B．‎ ‎【点评】本题考查集合的交、并、补的混合运算，基本知识的考查．‎ ‎　‎ ‎2．（5分）若实数x，y满足条件，则z=3x+y的最大值为（　　）‎ A．7 B．8 C．9 D．14‎ ‎【分析】作出不等式组对应的平面区域，利用目标函数的几何意义，求最大值．‎ ‎【解答】解：作出不等式组对应的平面区域如图：（阴影部分）．‎ 由z=3x+y得y=﹣3x+z，‎ 平移直线y=﹣3x+z，‎ 由图象可知当直线y=﹣3x+z经过点A时，直线y=﹣3x+z的截距最大，‎ 此时z最大．‎ 由，解得，即A（2，3），‎ 代入目标函数z=3x+y得z=3×2+3=9．‎ 即目标函数z=3x+y的最大值为9．‎ 故选：C．‎ ‎【点评】本题主要考查线性规划的应用，利用目标函数的几何意义，结合数形结合的数学思想是解决此类问题的基本方法．‎ ‎　‎ ‎3．（5分）阅读如图所示的程序框图，运行相应的程序，则输出i的值为（　　）‎ A．2 B．3 C．4 D．5‎ ‎【分析】模拟执行程序框图，依次写出每次循环得到的i，S的值，当S=0时满足条件S≤1，退出循环，输出i的值为4．‎ ‎【解答】解：模拟执行程序框图，可得 S=10，i=0‎ i=1，S=9‎ 不满足条件S≤1，i=2，S=7‎ 不满足条件S≤1，i=3，S=4‎ 不满足条件S≤1，i=4，S=0‎ 满足条件S≤1，退出循环，输出i的值为4．‎ 故选：C．‎ ‎【点评】本题主要考查了循环结构的程序框图，正确写出每次循环得到的i，S的值是解题的关键，属于基础题．‎ ‎　‎ ‎4．（5分）设x∈R，则“1＜x＜2”是“|x﹣2|＜1”的（　　）‎ A．充分而不必要条件 B．必要而不充分条件 C．充要条件 D．既不充分也不必要条件 ‎【分析】求解：|x﹣2|＜1，得出“1＜x＜2”，根据充分必要条件的定义判断即可．‎ ‎【解答】解：∵|x﹣2|＜1，‎ ‎∴1＜x＜3，‎ ‎∵“1＜x＜2”‎ ‎∴根据充分必要条件的定义可得出：“1＜x＜2”是“|x﹣2|＜1”的充分不必要条件．‎ 故选：A．‎ ‎【点评】本题考查了简单的不等式的求解，充分必要条件的定义，属于容易题．‎ ‎　‎ ‎5．（5分）已知双曲线﹣=1（a＞0，b＞0）的一个焦点为F（2，0），且双曲线的渐近线与圆（x﹣2）2+y2=3相切，则双曲线的方程为（　　）‎ A．﹣=1 B．﹣=1 C．﹣y2=1 D．x2﹣=1‎ ‎【分析】由题意可得双曲线的渐近线方程，根据圆心到切线的距离等于半径得，求出a，b的关系，结合焦点为F（2，0），求出a，b的值，即可得到双曲线的方程．‎ ‎【解答】解：双曲线的渐近线方程为bx±ay=0，‎ ‎∵双曲线的渐近线与圆（x﹣2）2+y2=3相切，‎ ‎∴，‎ ‎∴b=a，‎ ‎∵焦点为F（2，0），‎ ‎∴a2+b2=4，‎ ‎∴a=1，b=，‎ ‎∴双曲线的方程为x2﹣=1．‎ 故选：D．‎ ‎【点评】本题考查点到直线的距离公式，双曲线的标准方程，以及双曲线的简单性质的应用，求出a，b的值，是解题的关键．‎ ‎　‎ ‎6．（5分）如图，在圆O中，M、N是弦AB的三等分点，弦CD，CE分别经过点M，N，若CM=2，MD=4，CN=3，则线段NE的长为（　　）‎ A． B．3 C． D．‎ ‎【分析】由相交弦定理求出AM，再利用相交弦定理求NE即可．‎ ‎【解答】解：由相交弦定理可得CM•MD=AM•MB，‎ ‎∴2×4=AM•2AM，‎ ‎∴AM=2，‎ ‎∴MN=NB=2，‎ 又CN•NE=AN•NB，‎ ‎∴3×NE=4×2，‎ ‎∴NE=．‎ 故选：A．‎ ‎【点评】本题考查相交弦定理，考查学生的计算能力，比较基础．‎ ‎　‎ ‎7．（5分）已知定义在R上的函数f（x）=2|x﹣m|﹣1（m为实数）为偶函数，记a=f（log0.53），b=f（log25），c=f（2m），则a，b，c的大小关系为（　　）‎ A．a＜b＜c B．a＜c＜b C．c＜a＜b D．c＜b＜a ‎【分析】根据f（x）为偶函数便可求出m=0，从而f（x）=2|x|﹣1，这样便知道f（x）在[0，+∞）上单调递增，根据f（x）为偶函数，便可将自变量的值变到区间[0，+∞）上：a=f（|log0.53|），b=f（log25），c=f（0），然后再比较自变量的值，根据f（x）在[0，+∞）上的单调性即可比较出a，b，c的大小．‎ ‎【解答】解：∵f（x）为偶函数；‎ ‎∴f（﹣x）=f（x）；‎ ‎∴2|﹣x﹣m|﹣1=2|x﹣m|﹣1；‎ ‎∴|﹣x﹣m|=|x﹣m|；‎ ‎（﹣x﹣m）2=（x﹣m）2；‎ ‎∴mx=0；‎ ‎∴m=0；‎ ‎∴f（x）=2|x|﹣1；‎ ‎∴f（x）在[0，+∞）上单调递增，并且a=f（|log0.53|）=f（log23），b=f（log25），c=f（0）；‎ ‎∵0＜log23＜log25；‎ ‎∴c＜a＜b．‎ 故选：C．‎ ‎【点评】考查偶函数的定义，指数函数的单调性，对于偶函数比较函数值大小的方法就是将自变量的值变到区间[0，+∞）上，根据单调性去比较函数值大小．对数的换底公式的应用，对数函数的单调性，函数单调性定义的运用．‎ ‎　‎ ‎8．（5分）已知函数f（x）=，函数g（x）=3﹣f（2﹣x），则函数y=f（x）﹣g（x）的零点个数为（　　）‎ A．2 B．3 C．4 D．5‎ ‎【分析】求出函数y=f（x）﹣g（x）的表达式，构造函数h（x）=f（x）+f（2﹣x），作出函数h（x）的图象，利用数形结合进行求解即可．‎ ‎【解答】解：∵g（x）=3﹣f（2﹣x），‎ ‎∴y=f（x）﹣g（x）=f（x）﹣3+f（2﹣x），‎ 由f（x）﹣3+f（2﹣x）=0，得f（x）+f（2﹣x）=3，‎ 设h（x）=f（x）+f（2﹣x），‎ 若x≤0，则﹣x≥0，2﹣x≥2，‎ 则h（x）=f（x）+f（2﹣x）=2+x+x2，‎ 若0≤x≤2，则﹣2≤﹣x≤0，0≤2﹣x≤2，‎ 则h（x）=f（x）+f（2﹣x）=2﹣x+2﹣|2﹣x|=2﹣x+2﹣2+x=2，‎ 若x＞2，﹣x＜0，2﹣x＜0，‎ 则h（x）=f（x）+f（2﹣x）=（x﹣2）2+2﹣|2﹣x|=x2﹣5x+8．‎ 即h（x）=，‎ 作出函数h（x）的图象如图：‎ 当y=3时，两个函数有2个交点，‎ 故函数y=f（x）﹣g（x）的零点个数为2个，‎ 故选：A．‎ ‎【点评】本题主要考查函数零点个数的判断，根据条件求出函数的解析式，利用数形结合是解决本题的关键．‎ ‎　‎ 二、填空题：本大题共6小题，每小题5分，共30分．‎ ‎9．（5分）i是虚数单位，计算的结果为　﹣i　．‎ ‎【分析】直接利用复数的除法运算法则化简求解即可．‎ ‎【解答】解：i是虚数单位，‎ ‎===﹣i．‎ 故答案为：﹣i．‎ ‎【点评】本题考查复数的乘除运算，基本知识的考查．‎ ‎　‎ ‎10．（5分）一个几何体的三视图如图所示（单位：m），则该几何体的体积为　　m3．‎ ‎【分析】根据几何体的三视图，得出该几何体是圆柱与两个圆锥的组合体，结合图中数据求出它的体积．‎ ‎【解答】解：根据几何体的三视图，得；‎ 该几何体是底面相同的圆柱与两个圆锥的组合体，‎ 且圆柱底面圆的半径为1，高为2，圆锥底面圆的半径为1，高为1；‎ ‎∴该几何体的体积为 V几何体=2×π•12×1+π•12•2‎ ‎=π．‎ 故答案为：π．‎ ‎【点评】本题考查了利用空间几何体的三视图求体积的应用问题，是基础题目．‎ ‎　‎ ‎11．（5分）已知函数f（x）=axlnx，x∈（0，+∞），其中a为实数，f′（x）为f（x）的导函数，若f′（1）=3，则a的值为　3　．‎ ‎【分析】由题意求出f'（x），利用f′（1）=3，求a．‎ ‎【解答】解：因为f（x）=axlnx，所以f′（x）=f（x）=lna•axlnx+ax，又f′（1）=3，所以a=3；‎ 故答案为：3．‎ ‎【点评】本题考查了求导公式的运用；熟练掌握求导公式是关键．‎ ‎　‎ ‎12．（5分）已知a＞0，b＞0，ab=8，则当a的值为　4　时，log2a•log2‎ ‎（2b）取得最大值．‎ ‎【分析】由条件可得a＞1，再利用基本不等式，求得当a=4时，log2a•log2（2b）取得最大值，从而得出结论．‎ ‎【解答】解：由题意可得当log2a•log2（2b）最大时，log2a和log2（2b）都是正数，‎ 故有a＞1．‎ 再利用基本不等式可得log2a•log2（2b）≤===4，‎ 当且仅当a=2b=4时，取等号，即当a=4时，log2a•log2（2b）取得最大值，‎ 故答案为：4．‎ ‎【点评】本题主要考查基本不等式的应用，注意检查等号成立条件以及不等式的使用条件，属于中档题．‎ ‎　‎ ‎13．（5分）在等腰梯形ABCD中，已知AB∥DC，AB=2，BC=1，∠ABC=60°，点E和F分别在线段BC和DC上，且=，=，则•的值为　　．‎ ‎【分析】根据向量数量积的公式和应用，进行运算求解即可．‎ ‎【解答】解：∵AB=2，BC=1，∠ABC=60°，‎ ‎∴BG==，CD=2﹣1=1，∠BCD=120°，‎ ‎∵=，=，‎ ‎∴•=（+）•（+）=（+）•（+）‎ ‎=•+•+•+•‎ ‎=2×1×cos60°+×2×1×cos0°+×1×1×cos60°+××1×1×cos120°‎ ‎=1+=，‎ 故答案为：‎ ‎【点评】本题主要考查向量数量积的应用，根据条件确定向量的长度和夹角是解决本题的关键．‎ ‎　‎ ‎14．（5分）已知函数f（x）=sinωx+cosωx（ω＞0），x∈R，若函数f（x）在区间（﹣ω，ω）内单调递增，且函数y=f（x）的图象关于直线x=ω对称，则ω的值为　　．‎ ‎【分析】由两角和的正弦函数公式化简解析式可得f（x）=sin（ωx+），由2kπ﹣≤ωx+≤2kπ+，k∈Z可解得函数f（x）的单调递增区间，结合已知可得：﹣ω≥①，ω≤②，k∈Z，从而解得k=0，又由ωx+=kπ+，可解得函数f（x）的对称轴为：x=，k∈Z，结合已知可得：ω2=，从而可求ω的值．‎ ‎【解答】解：∵f（x）=sinωx+cosωx=sin（ωx+），‎ ‎∵函数f（x）在区间（﹣ω，ω）内单调递增，ω＞0‎ ‎∴2kπ﹣≤ωx+≤2kπ+，k∈Z可解得函数f（x）的单调递增区间为：[，]，k∈Z，‎ ‎∴可得：﹣ω≥①，ω≤②，k∈Z，‎ ‎∴解得：0＜ω2≤且0＜ω2≤2k，k∈Z，‎ 解得：﹣，k∈Z，‎ ‎∴可解得：k=0，‎ 又∵由ωx+=kπ+，可解得函数f（x）的对称轴为：x=，k∈Z，‎ ‎∴由函数y=f（x）的图象关于直线x=ω对称，可得：ω2=，可解得：ω=．‎ 故答案为：．‎ ‎【点评】本题主要考查了由y=Asin（ωx+φ）的部分图象确定其解析式，考查了正弦函数的图象和性质，正确确定k的值是解题的关键，属于中档题．‎ ‎　‎ 三、解答题：本大题共6小题，共80分，解答应写出文字说明，证明过程或演算步骤．‎ ‎15．（13分）设甲、乙、丙三个乒乓球协会的运动员人数分别为27，9，18，先采用分层抽取的方法从这三个协会中抽取6名运动员组队参加比赛．‎ ‎（Ⅰ）求应从这三个协会中分别抽取的运动员的人数；‎ ‎（Ⅱ）将抽取的6名运动员进行编号，编号分别为A1，A2，A3，A4，A5，A6，现从这6名运动员中随机抽取2人参加双打比赛．‎ ‎（i）用所给编号列出所有可能的结果；‎ ‎（ii）设A为事件“编号为A5和A6的两名运动员中至少有1人被抽到”，求事件A发生的概率．‎ ‎【分析】（Ⅰ）由题意可得抽取比例，可得相应的人数；‎ ‎（Ⅱ）（i）列举可得从6名运动员中随机抽取2名的所有结果共15种；‎ ‎（ii）事件A包含上述9个，由概率公式可得．‎ ‎【解答】解：（Ⅰ）由题意可得抽取比例为=，‎ ‎27×=3，9×=1，18×=2，‎ ‎∴应甲、乙、丙三个协会中分别抽取的运动员的人数为3、1、2；‎ ‎（Ⅱ）（i）从6名运动员中随机抽取2名的所有结果为：‎ ‎（A1，A2），（A1，A3），（A1，A4），（A1，A5），（A1，A6），‎ ‎（A2，A3），（A2，A4），（A2，A5），（A2，A6），（A3，A4），‎ ‎（A3，A5），（A3，A6），（A4，A5），（A4，A6），（A5，A6），‎ 共15种；‎ ‎（ii）设A为事件“编号为A5和A6的两名运动员中至少有1人被抽到”，‎ 则事件A包含：（A1，A5），（A1，A6），（A2，A5），（A2，A6），‎ ‎（A3，A5），（A3，A6），（A4，A5），（A4，A6），（A5，A6）共9个基本事件，‎ ‎∴事件A发生的概率P==‎ ‎【点评】本题考查古典概型及其概率公式，涉及分层抽样，属基础题．‎ ‎　‎ ‎16．（13分）在△ABC中，内角A，B，C所对的边分别为a，b，c，已知△ABC的面积为3，b﹣c=2，cosA=﹣．‎ ‎（Ⅰ）求a和sinC的值；‎ ‎（Ⅱ）求cos（2A+）的值．‎ ‎【分析】（Ⅰ）通过三角形的面积以及已知条件求出b，c，利用正弦定理求解sinC的值；‎ ‎（Ⅱ）利用两角和的余弦函数化简cos（2A+），然后直接求解即可．‎ ‎【解答】解：（Ⅰ）在三角形ABC中，由cosA=﹣，可得sinA=，△ABC的面积为3，可得：，‎ 可得bc=24，又b﹣c=2，解得b=6，c=4，由a2=b2+c2﹣2bccosA，可得a=8，‎ ‎，解得sinC=；‎ ‎（Ⅱ）cos（2A+）=cos2Acos﹣sin2Asin==．‎ ‎【点评】本题考查同角三角函数的基本关系式，二倍角公式，余弦定理的应用，考查计算能力．‎ ‎　‎ ‎17．（13分）如图，已知AA1⊥平面ABC，BB1∥AA1，AB=AC=3，BC=2，AA1=，BB1=2，点E和F分别为BC和A1C的中点．‎ ‎（Ⅰ）求证：EF∥平面A1B1BA；‎ ‎（Ⅱ）求证：平面AEA1⊥平面BCB1；‎ ‎（Ⅲ）求直线A1B1与平面BCB1所成角的大小．‎ ‎【分析】（Ⅰ）连接A1B，易证EF∥A1B，由线面平行的判定定理可得；‎ ‎（Ⅱ）易证AE⊥BC，BB1⊥AE，可证AE⊥平面BCB1，进而可得面面垂直；‎ ‎（Ⅲ）取BB1中点M和B1C中点N，连接A1M，A1N，NE，易证∠A1B1N即为直线A1B1与平面BCB1所成角，解三角形可得．‎ ‎【解答】（Ⅰ）证明：连接A1B，在△A1BC中，‎ ‎∵E和F分别是BC和A1C的中点，∴EF∥A1B，‎ 又∵A1B⊂平面A1B1BA，EF⊄平面A1B1BA，‎ ‎∴EF∥平面A1B1BA；‎ ‎（Ⅱ）证明：∵AB=AC，E为BC中点，∴AE⊥BC，‎ ‎∵AA1⊥平面ABC，BB1∥AA1，∴BB1⊥平面ABC，‎ ‎∴BB1⊥AE，又∵BC∩BB1=B，∴AE⊥平面BCB1，‎ 又∵AE⊂平面AEA1，∴平面AEA1⊥平面BCB1；‎ ‎（Ⅲ）取BB1中点M和B1C中点N，连接A1M，A1N，NE，‎ ‎∵N和E分别为B1C和BC的中点，∴NE平行且等于B1B，‎ ‎∴NE平行且等于A1A，∴四边形A1AEN是平行四边形，‎ ‎∴A1N平行且等于AE，‎ 又∵AE⊥平面BCB1，∴A1N⊥平面BCB1，‎ ‎∴∠A1B1N即为直线A1B1与平面BCB1所成角，‎ 在△ABC中，可得AE=2，∴A1N=AE=2，‎ ‎∵BM∥AA1，BM=AA1，∴A1M∥AB且A1M=AB，‎ 又由AB⊥BB1，∴A1M⊥BB1，‎ 在RT△A1MB1中，A1B1==4，‎ 在RT△A1NB1中，sin∠A1B1N==，‎ ‎∴∠A1B1N=30°，即直线A1B1与平面BCB1所成角的大小为30°‎ ‎【点评】本题考查线面垂直与平行关系的证明，涉及直线与平面所成的角，属中档题．‎ ‎　‎ ‎18．（13分）已知{an}是各项均为正数的等比数列，{bn}是等差数列，且a1=b1=1，b2+b3=2a3，a5﹣3b2=7．‎ ‎（Ⅰ）求{an}和{bn}的通项公式；‎ ‎（Ⅱ）设cn=anbn，n∈N*，求数列{cn}的前n项和．‎ ‎【分析】（Ⅰ）设出数列{an}的公比和数列{bn}的公差，由题意列出关于q，d的方程组，求解方程组得到q，d的值，则等差数列和等比数列的通项公式可求；‎ ‎（Ⅱ）由题意得到，然后利用错位相减法求得数列{cn}的前n项和．‎ ‎【解答】解：（Ⅰ）设数列{an}的公比为q，数列{bn}的公差为d，由题意，q＞0，‎ 由已知有，消去d整理得：q4﹣2q2﹣8=0．‎ ‎∵q＞0，解得q=2，∴d=2，‎ ‎∴数列{an}的通项公式为，n∈N*；‎ 数列{bn}的通项公式为bn=2n﹣1，n∈N*．‎ ‎（Ⅱ）由（Ⅰ）有，‎ 设{cn}的前n项和为Sn，则 ‎，‎ ‎，‎ 两式作差得：=2n+1﹣3﹣（2n﹣1）×2n=﹣（2n﹣3）×2n﹣3．‎ ‎∴．‎ ‎【点评】本题主要考查等差数列、等比数列及其前n项和，考查数列求和的基本方法和运算求解能力，是中档题．‎ ‎　‎ ‎19．（14分）已知椭圆+=1（a＞b＞0）的上顶点为B，左焦点为F，离心率为．‎ ‎（Ⅰ）求直线BF的斜率．‎ ‎（Ⅱ）设直线BF与椭圆交于点P（P异于点B），过点B且垂直于BP的直线与椭圆交于点Q（Q异于点B），直线PQ与y轴交于点M，|PM|=λ|MQ|．‎ ‎（i）求λ的值．‎ ‎（ii）若|PM|sin∠BQP=，求椭圆的方程．‎ ‎【分析】（Ⅰ）通过e=、a2=b2+c2、B（0，b），计算即得结论；‎ ‎（Ⅱ）设点P（xP，yP），Q（xQ，yQ），M（xM，yM ‎）．（i）通过（I），联立直线BF与椭圆方程，利用韦达定理可得xP=﹣，利用BQ⊥BP，联立直线BQ与椭圆方程，通过韦达定理得xQ=，计算即得结论；（ii）通过=可得|PQ|=|PM|，利用|PM|sin∠BQP=，可得|BP|=，通过yP=2xP+2c=﹣c计算可得c=1，进而可得结论．‎ ‎【解答】解：（Ⅰ）设左焦点F（﹣c，0），‎ ‎∵离心率e=，a2=b2+c2，∴a=c，b=2c，‎ 又∵B（0，b），∴直线BF的斜率k===2；‎ ‎（Ⅱ）设点P（xP，yP），Q（xQ，yQ），M（xM，yM）．‎ ‎（i）由（I）知a=c，b=2c，kBF=2，‎ ‎∴椭圆方程为+=1，直线BF方程为y=2x+2c，‎ 联立直线BF与椭圆方程，消去y并整理得：3x2+5cx=0，解得xP=﹣，‎ ‎∵BQ⊥BP，∴直线BQ的方程为：y=﹣x+2c，‎ 联立直线BQ与椭圆方程，消去y并整理得：21x2﹣40cx=0，解得xQ=，‎ 又∵λ=，及xM=0，∴λ===；‎ ‎（ii）∵=，∴==，即|PQ|=|PM|，‎ 又∵|PM|sin∠BQP=，∴|BP|=|PQ|sin∠BQP=|PM|sin∠BQP=，‎ 又∵yP=2xP+2c=﹣c，∴|BP|==c，‎ 因此=c，即c=1，‎ ‎∴椭圆的方程为：+=1．‎ ‎【点评】本题考查椭圆的标准方程与几何性质、直线的方程、两条直线垂直等基础知识，考查用代数方法研究圆锥曲线的性质，考查运算求解能力以及用方程思想和化归思想解决问题的能力，属于中档题．‎ ‎　‎ ‎20．（14分）已知函数f（x）=4x﹣x4，x∈R．‎ ‎（Ⅰ）求f（x）的单调区间；‎ ‎（Ⅱ）设曲线y=f（x）与x轴正半轴的交点为P，曲线在点P处的切线方程为y=g（x），求证：对于任意的实数x，都有f（x）≤g（x）；‎ ‎（Ⅲ）若方程f（x）=a（a为实数）有两个实数根x1，x2，且x1＜x2，求证：x2﹣x1≤﹣+4．‎ ‎【分析】（Ⅰ）求出原函数的导函数，得到导函数的零点，由零点对定义域分段，根据导函数在各区间段内的符号得到原函数的单调性；‎ ‎（Ⅱ）设出点p的坐标，利用导数求出切线方程g（x）=f′（x0）（x﹣x0），构造辅助函数F（x）=f（x）﹣g（x），利用导数得到对于任意实数x，‎ 有F（x）≤F（x0）=0，即对任意实数x，都有f（x）≤g（x）；‎ ‎（Ⅲ）由（Ⅱ）知，，求出方程g（x）=a的根，由g（x）在（﹣∞，+∞）上单调递减，得到x2≤x2′．‎ 同理得到x1′≤x1，则可证得．‎ ‎【解答】（Ⅰ）解：由f（x）=4x﹣x4，可得f′（x）=4﹣4x3．‎ 当f′（x）＞0，即x＜1时，函数f（x）单调递增；‎ 当f′（x）＜0，即x＞1时，函数f（x）单调递减．‎ ‎∴f（x）的单调递增区间为（﹣∞，1），单调递减区间为（1，+∞）．‎ ‎（Ⅱ）证明：设点p的坐标为（x0，0），则，f′（x0）=﹣12，‎ 曲线y=f（x）在点P处的切线方程为y=f′（x0）（x﹣x0），即g（x）=f′（x0）（x﹣x0），‎ 令函数F（x）=f（x）﹣g（x），即F（x）=f（x）﹣f′（x0）（x﹣x0），‎ 则F′（x）=f′（x）﹣f′（x0）．‎ ‎∵F′（x0）=0，∴当x∈（﹣∞，x0）时，F′（x）＞0；当x∈（x0，+∞）时，F′（x）＜0，‎ ‎∴F（x）在（﹣∞，x0）上单调递增，在（x0，+∞）上单调递减，‎ ‎∴对于任意实数x，F（x）≤F（x0）=0，即对任意实数x，都有f（x）≤g（x）；‎ ‎（Ⅲ）证明：由（Ⅱ）知，，设方程g（x）=a的根为x2′，可得．‎ ‎∵g（x）在（﹣∞，+∞）上单调递减，又由（Ⅱ）知g（x2）≥f（x2）=a=g（x2′），‎ 因此x2≤x2′．‎ 类似地，设曲线y=f（x）在原点处的切线方程为y=h（x），可得h（x）=4x，‎ 对于任意的x∈（﹣∞，+∞），有f（x）﹣h（x）=﹣x4≤0，即f（x）≤h（x）．‎ 设方程h（x）=a的根为x1′，可得，‎ ‎∵h（x）=4x在（﹣∞，+∞）上单调递增，且h（x1′）=a=f（x1）≤h（x1），‎ 因此x1′≤x1，‎ 由此可得．‎ ‎【点评】本小题主要考查导数的运算、导数的几何意义、利用导数研究函数的性质等基础知识．考查函数思想、化归思想，考查综合分析问题和解决问题的能力，是压轴题．‎ ‎　‎