高考数学一轮复习第二章函数及其应用2-1函数及其表示练习理北师大版 9页

‎2.1 函数及其表示 核心考点·精准研析 考点一　函数的定义域 ‎ ‎1.函数y=的定义域是 (　　)‎ A.(-1,3) B.(-1,3]‎ C.(-1,0)∪(0,3)　　 D.(-1,0)∪(0,3]‎ ‎2.若函数y=f(x)的定义域是[0,2 020],则函数g(x)=f(x+1)(x≠1)的定义域是 (　　)‎ A.[-1,2 019] B.[-1,1)∪(1,2 019]‎ C.[0,2 020] D.[-1,1)∪(1,2 020]‎ ‎3.(2020·抚州模拟)若函数f(x)的定义域为[0,6],则函数的定义域为 ‎ ‎ (　　)‎ A.(0,3) B.[1,3)∪(3,8]‎ C.[1,3) D.[0,3)‎ ‎4.函数f(x)=lg+(4-x)0的定义域为________. ‎ ‎　【解析】1.选D.由题意得 解得-12且x≠3且x≠4,所以函数的定义域为(2,3)∪(3,4)∪(4,+∞).‎ 答案:(2,3)∪(3,4)∪(4,+∞)‎ ‎　题2中,若将“函数y=f(x)的定义域是[0,2 020]”改为“函数y=f(x-1)的定义域是[0,2 020]”,则函数g(x)=f(x+1)(x≠1)的定义域为__________. ‎ ‎【解析】由0≤x≤2 020,得-1≤x-1≤2 019,再由-1≤x+1≤2 019,解得-2≤x≤2 018,又因为x≠1,所以函数g(x)的定义域是[-2,1)∪(1,2 018].‎ 答案:[-2,1)∪(1,2 018]‎ ‎1.具体函数y=f(x)的定义域 序号 f(x)解析式 定义域 ‎1‎ 整式 R ‎2‎ 分式 分母≠0‎ ‎3‎ 偶次根式 被开方数≥0‎ ‎4‎ 奇次根式 被开方数∈R ‎5‎ 指数式 幂指数∈R ‎6‎ 对数式 真数>0;底数>0且≠1‎ ‎7‎ y=x0‎ 底数x≠0‎ ‎2.抽象函数(没有解析式的函数)的定义域 解题方法:精髓是“换元法”,即将括号内看作整体,关键是看求x还是求整体的取值范围.‎ ‎(1)已知y=f(x)的定义域是A,求y=f(g(x))的定义域:可由g(x)∈A,求出x的范围,即为y=f(g(x))的定义域.‎ ‎(2)已知y=f(g(x))的定义域是A,求y=f(x)的定义域:可由x∈A求出g(x)的范围,即为y=f(x)的定义域.‎ ‎【秒杀绝招】‎ ‎　排除法解T1,可依据选项的特点,将0,3代入验证.‎ - 9 -‎ 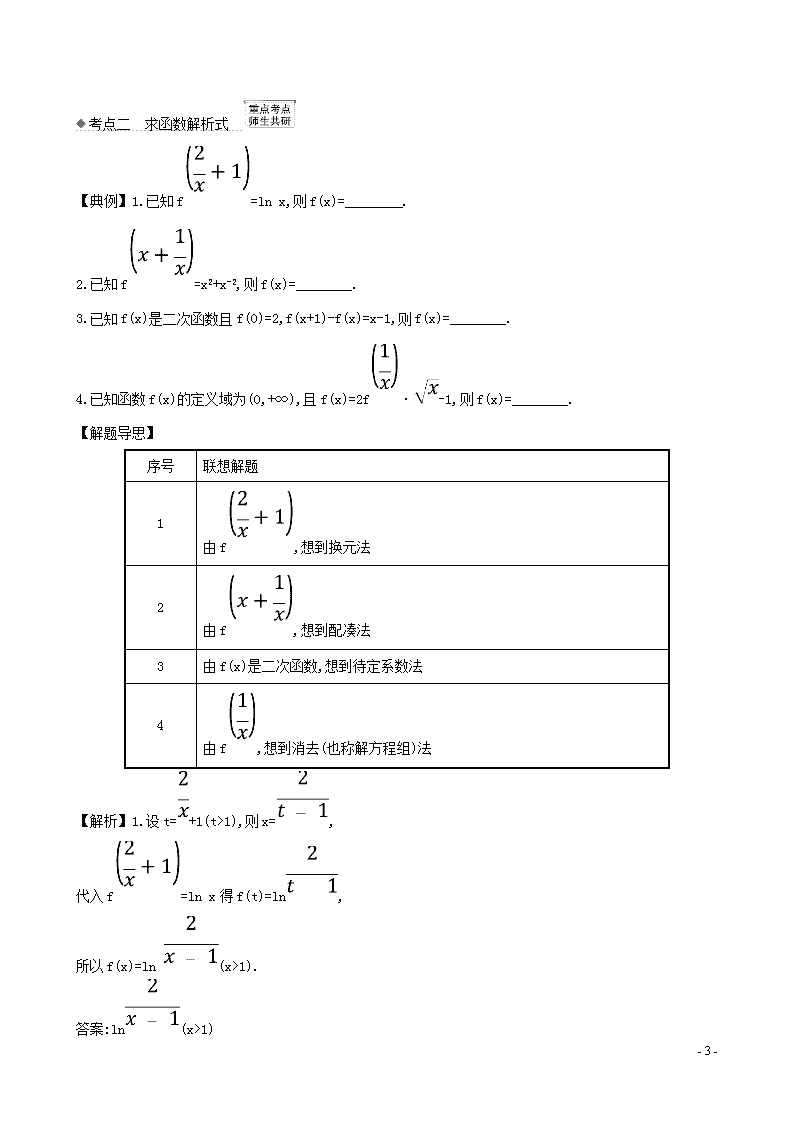考点二　求函数解析式 ‎ ‎【典例】1.已知f=ln x,则f(x)=________. ‎ ‎2.已知f=x2+x-2,则f(x)=________. ‎ ‎3.已知f(x)是二次函数且f(0)=2,f(x+1)-f(x)=x-1,则f(x)=________. ‎ ‎4.已知函数f(x)的定义域为(0,+∞),且f(x)=2f·-1,则f(x)=________.‎ ‎【解题导思】‎ 序号 联想解题 ‎1‎ 由f,想到换元法 ‎2‎ 由f,想到配凑法 ‎3‎ 由f(x)是二次函数,想到待定系数法 ‎4‎ 由f,想到消去(也称解方程组)法 ‎【解析】1.设t=+1(t>1),则x=,‎ 代入f=ln x得f(t)=ln,‎ 所以f(x)=ln (x>1).‎ 答案:ln(x>1)‎ - 9 -‎ ‎2.因为f=x2+x-2=-2,‎ 又因为x+≤-2或x+≥2,‎ 所以f(x)=x2-2(x≤-2或x≥2).‎ 答案:x2-2(x≤-2或x≥2) ‎ ‎3.设f(x)=ax2+bx+c(a≠0),由f(0)=2,得c=2,‎ f(x+1)-f(x)=a(x+1)2+b(x+1)+2-ax2-bx-2=x-1,即2ax+a+b=x-1,‎ 所以即 所以f(x)=x2-x+2.‎ 答案:x2-x+2‎ ‎4.在f(x)=2f·-1中,将x换成,则换成x,得f=2f(x)·-1,‎ 由解得f(x)=+.‎ 答案:+‎ ‎　 函数解析式的求法 ‎(1)待定系数法:若已知函数的类型,可用待定系数法.‎ ‎(2)换元法:已知复合函数f(g(x))的解析式,可用换元法,此时要注意新元的取值范围.‎ - 9 -‎ ‎(3)配凑法:由已知条件f(g(x))=F(x),可将F(x)改写成关于g(x)的表达式,然后以x替代g(x),便得f(x)的解析式.‎ ‎(4)消去(方程组)法:已知f(x)与f或f(-x)之间的关系式,可根据已知条件再构造出另外一个等式组成方程组,通过解方程组求出f(x).‎ ‎1.若函数f(x)=2x+3,g(x+2)=f(x),则g(x)的解析式为________. ‎ ‎【解析】方法一(换元法):‎ 由题意知g(x+2)=2x+3,令t=x+2,则x=t-2,所以g(t)=2(t-2)+3=2t-1,所以g(x)=2x-1,‎ 答案:g(x)=2x-1‎ 方法二(配凑法):‎ 由题意知g(x+2)=2x+3=2(x+2)-1.‎ 所以g(x)=2x-1.‎ 答案:g(x)=2x-1‎ ‎2.已知f(x)是一次函数,且满足3f(x+1)-2f(x-1)=2x+17,则f(x)=________. ‎ ‎【解析】设f(x)=ax+b(a≠0),‎ 则3f(x+1)-2f(x-1)=ax+5a+b,‎ 所以ax+5a+b=2x+17对任意实数x都成立,‎ 所以解得 所以f(x)=2x+7.‎ 答案:2x+7‎ 考点三　分段函数及其应用 ‎ 命 题 精 解 读 ‎1.考什么:(1)考查求函数值、解方程、解不等式等问题.(2)考查数学运算、数学抽象、直观想象等核心素养.‎ ‎2.怎么考:基本初等函数、函数的单调性、不等式交汇考查函数的概念、图像等知识.‎ ‎3.新趋势:以基本初等函数为载体,与其他知识交汇考查为主.‎ - 9 -‎ 学 霸 好 方 法 ‎1.求值问题的解题思路 ‎(1)求函数值:当出现f(f(x))的形式时,应从内到外依次求值.‎ ‎(2)求自变量的值:依据题设条件,在各段上得出关于自变量的方程,然后求出相应自变量的值.‎ ‎2.交汇问题:与方程、不等式交汇时,要依据“分段问题,分段解决”进行讨论,最后将结果并起来.‎ 分段函数的求值问题 ‎【典例】已知f(x)=则f+f的值为 (　　)‎ A.　　　 B.-　　　 C.-1　　　 D.1‎ ‎【解析】选D.f+f=f+1+‎ f=cos+1+cos=1.‎ 如何求分段函数的函数值?‎ 提示:分段函数求函数值时,要根据自变量选取函数解析式,然后再代入.‎ 分段函数与方程问题 ‎【典例】已知函数f(x)=且f(a)=-3,则f(6-a)= ‎ ‎ (　　)‎ A.- B.- C.- D.-‎ ‎【解析】选A.当a≤1时不符合题意,所以a>1,‎ 即-log2(a+1)=-3,解得a=7,‎ - 9 -‎ 所以f(6-a)=f(-1)=2-2-2=-.‎ 求分段函数含有参数的函数值,如何列方程?‎ 提示:列方程时,若自变量的范围确定时,则直接代入;若不确定,则需要分类讨论.‎ 分段函数与不等式问题 ‎【典例】(2017·全国卷Ⅲ)设函数f(x)=则满足f(x)+f>1的x的取值范围是________. ‎ ‎【解析】令g(x)=f(x)+f,‎ 当x≤0时,g(x)=f(x)+f=2x+;‎ 当0时,g(x)=f(x)+f=2x-1,‎ 写成分段函数的形式:g(x)=f(x)+f=函数g(x)在区间(-∞,0],,三段区间内均连续单调递增,且g=1,20+0+>1,(+2)×20-1>1,‎ - 9 -‎ 可知x的取值范围是.‎ 答案:‎ 如何求解由分段函数构成的不等式?‎ 提示:求解分段函数构成的不等式,关键是确定自变量在分段函数的哪一段,用对解析式.‎ ‎1.设函数f(x)=则f(-2)+f(log212)= (　　)‎ A.3　　 B.6　　　 C.9　　　 D.12‎ ‎【解析】选C.因为函数f(x)=‎ 所以f(-2)=1+log2(2+2)=1+2=3,‎ f(log212)==×=12×=6,则有f(-2)+f(log212)=3+6=9.‎ ‎2.(2020·长沙模拟)已知函数f(x)=那么f(f(-3))=________. ‎ ‎【解析】由已知得f(-3)=2-(-3)=5,从而f(f(-3))=f(5)=52=25.‎ 答案:25‎ ‎1.已知函数f(x)的定义域为(-∞,+∞),如果f(x+2 020)=那么f·f= (　　)‎ A.2 020 B. C.4 D.‎ - 9 -‎ ‎【解析】选C.当x≥0时,有f=sin x,‎ 所以f=sin =1,‎ 当x<0时,f=lg(-x),‎ 所以f(-7 980)=f(-10 000+2 020)=lg10 000=4,‎ f·f=1×4=4.‎ ‎2.在一个展现人脑智力的综艺节目中,一位参加节目的少年能将圆周率π准确地记忆到小数点后面200位,更神奇的是当主持人说出小数点后面的位数时,这位少年都能准确地说出该数位上的数字.如果记圆周率π小数点后第n位上的数字为y.那么你认为y是n的函数吗?如果是,请写出函数的定义域、值域与对应关系.如果不是,请说明理由.‎ ‎【解析】y是n的函数.理由如下:n任取一个数字,就有0到9之间的一个数字与之对应,符合函数的定义,所以函数的定义域是{1,2,3,4,…,n}(其中n是圆周率小数点后面的位数);值域是{0,1,2,3,4,5,6,7,8,9};对应关系是y与π的小数点后第n位上的数字对应.‎ - 9 -‎