2020届高考文科数学二轮专题复习课件：专题4 立体几何2-4-解答题 1 59页

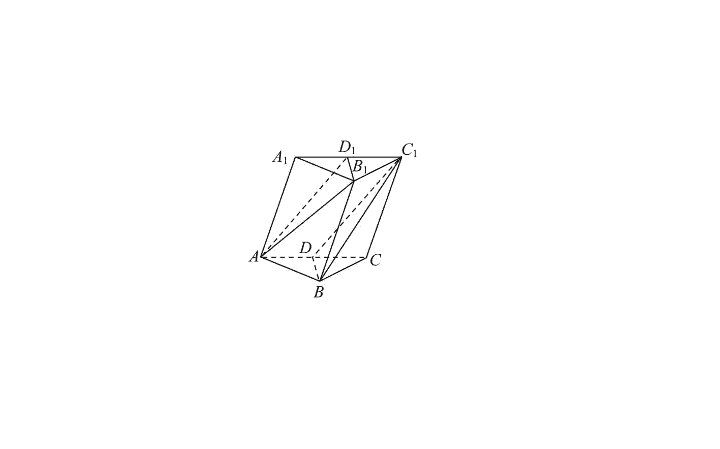
第 1 课时 　 平行与垂直的证明 考向一　 空间中的平行关系 角度 1 　直线与平面平行的判定与性质 【例 1 】 (2019 · 宜昌一模 ) 如图所示 , 斜三棱柱 ① ABC-A 1 B 1 C 1 中 , 点 D ， D1 分别为 AC ， A 1 C1 的中点 ② . (1) 证明 AD 1 ∥ 平面 BDC 1 . ③ (2) 证明 BD∥ 平面 AB 1 D 1 . 【题眼直击 】 题眼 思维导引 ① 想到各个侧面均为平行四边形 ② 想到 A 1 D 1 =D 1 C 1 ,AD=DC ③ 想到线面平行的判定定理 【解析 】 (1) 因为 D 1 ,D 分别为 A 1 C 1 与 AC 的中点 , 四边形 ACC 1 A 1 为平行四边形 , 所以 C 1 D 1 ∥DA,C 1 D 1 =DA, 所以四边形 ADC 1 D 1 为平行四边形 , 所以 AD 1 ∥C 1 D. 又 AD 1 ⊄ 平面 BDC 1 ,C 1 D⊂ 平面 BDC 1 , 所以 AD 1 ∥ 平面 BDC 1 . (2) 连接 D 1 D. 因为 BB 1 ∥ 平面 ACC 1 A 1 , BB 1 ⊂ 平面 BB 1 D 1 D, 平面 ACC 1 A 1 ∩ 平面 BB 1 D 1 D=D 1 D, 所以 BB 1 ∥D 1 D. 又 D 1 ,D 分别为 A 1 C 1 ,AC 的中点 , 所以 BB 1 =DD 1 , 所以四边形 BDD 1 B 1 为平行四边形 , 所以 BD∥B 1 D 1 . 又 BD⊄ 平面 AB 1 D 1 ,B 1 D 1 ⊂ 平面 AB 1 D 1 , 所以 BD∥ 平面 AB 1 D 1 . 【拓展提升 】 证明线面平行问题的思路 ( 一 ) (1) 作 ( 找 ) 出所证线面平行中的平面内的一条直线 . (2) 证明线线平行 . (3) 根据线面平行的判定定理证明线面平行 . 证明线面平行问题的思路 ( 二 ) (1) 在多面体中作出要证线面平行中的线所在的平面 . (2) 利用线面平行的判定定理证明所作平面内的两条相交直线分别与所证平面平行 . (3) 证明所作平面与所证平面平行 . (4) 转化为线面平行 . 【变式训练 】 1. 将本例条件“ D,D 1 分别为 AC,A 1 C 1 的中点”变为 “ D,D 1 分别为 AC,A 1 C 1 上的点” . 试问当 等于何值 时 ,BC 1 ∥ 平面 AB 1 D 1 . 【解析 】 如图 , 取 D 1 为线段 A 1 C 1 的中点 , 此时 =1, 连接 A 1 B 交 AB 1 于点 O, 连接 OD 1 , 由棱柱的性质知四边形 A 1 ABB 1 为平 行四边形 , 所以 O 为 A 1 B 的中点 . 在 △ A 1 BC 1 中 , 点 O,D 1 分别为 A 1 B,A 1 C 1 的中点 , 所以 OD 1 ∥BC 1 , 又 OD 1 ⊂ 平面 AB 1 D 1 ,BC 1 ⊄ 平面 AB 1 D 1 , 所以 BC 1 ∥ 平面 AB 1 D 1 , 所以当 =1 时 ,BC 1 ∥ 平面 AB 1 D 1 . 2. 将本例条件“ D,D 1 分别为 AC,A 1 C 1 的中点”变为 “ D,D 1 分别为 AC,A 1 C 1 上的点且平面 BC 1 D∥ 平面 AB 1 D 1 ”, 试求 的值 . 【解析 】 由平面 BC 1 D∥ 平面 AB 1 D 1 , 且平面 A 1 BC 1 ∩ 平面 BC 1 D=BC 1 , 平面 A 1 BC 1 ∩ 平面 AB 1 D 1 =D 1 O 得 BC 1 ∥D 1 O, 所以 . 又 , =1, 所以 =1, 即 =1. 角度 2 　平面与平面平行的判定与性质 【例 2 】 (2019 · 信阳一模 ) 如图 , 在三棱柱 ABC-A 1 B 1 C 1 中 ,E,F,G,H 分别是 AB,AC,A 1 B 1 ,A 1 C 1 的中点 , 求证 : 世纪金榜导学号 (1) B ， C ， H ， G 四点共面 ① . (2) 平面 EFA1∥ 平面 BCHG ② . 【题眼直击 】 题眼 思维导引 ① 想到证明 GH∥BC ② 根据面面平行的判定定理证明 【解析 】 (1) 因为 G,H 分别是 A 1 B 1 ,A 1 C 1 的中点 , 所以 GH 是 △ A 1 B 1 C 1 的中位线 , 所以 GH∥B 1 C 1 . 又因为 B 1 C 1 ∥BC, 所以 GH∥BC, 所以 B,C,H,G 四点共面 . (2) 因为 E,F 分别是 AB,AC 的中点 , 所以 EF∥BC. 因为 EF ⊄ 平面 BCHG,BC ⊂ 平面 BCHG, 所以 EF∥ 平面 BCHG. 因为 A 1 G