【精品试题】2021年高考数学一轮复习创优测评卷（新高考专用）测试卷08 立体几何（原卷版） 7页

2021 年高考数学一轮复习立体几何创优测评卷(新高考专用) 一、单选题（共 60 分，每题 5 分） 1．在平面几何中，有“若 ABC 的周长 c ，面积为 S ，则内切圆半径 2Sr c  ”，类比上述结论，在立体 几何中，有“若四面体 ABCD的表面积为 S ，体积为V ，则其内切球的半径 r  （ ） A． 3V S B． 2V S C． 2 V S D． 3 V S 2．在立体几何中，以下命题中假命题的个数为（ ） ①若直线 / /a b ，b  平面 ，则 / /a  . ②若平面  平面 ，平面   平面 ， l   ，则l  . ③有 3 个角是直角的四边形是矩形. ④若平面  平面  ， a  平面 ，b  平面  ，且 a b r r ，则 a  . A．0 个 B．1 个 C．2 个 D．3 个 3．在立体几何中，用一个平面去截一个几何体得到的平面图形叫截面. 如图，在棱长为 1 的正方体 1 1 1 1ABCD A B C D 中，点 ,E F 分别是棱 1 1 1,B B BC 的中点，点G 是棱 1CC 的中点，则过线段 AG 且平行于 平面 1A EF 的截面的面积为（ ） A．1 B． 9 8 C． 8 9 D． 2 4．如图（1）（2）（3）（4）为四个几何体的三视图，根据三视图可知这四个几何体依次分别为（ ） A．三棱台、三棱柱、圆锥、圆台 B．三棱柱、正四棱锥、圆锥、圆台 C．三棱柱、三棱台、圆锥、圆台 D．三棱柱、三棱锥、圆锥、圆台 5．已知正方体的棱长为 1，平面 过正方体的一个顶点，且与正方体每条棱所在直线所成的角相等，则该 正方体在平面 内的正投影面积是（ ） A． 3 3 2 B． 3 C． 2 D． 3 3 4 6．α，β是两个不重合的平面，下面说法中，正确的是( ) A．平面α内有两条直线 a，b 都与平面β平行，那么α∥β B．平面α内有无数条直线平行于平面β，那么α∥β C．若直线 a 与平面α和平面β都平行，那么α∥β D．平面α内所有的直线都与平面β平行，那么α∥β 7．在三棱锥 P ABC 中，已知 PA AB AC  ， BAC PAC   ，点 D ， E 分别为棱 BC ， PC 的中 点，则下列结论正确的是 ( )A．直线 DE  直线 AD B．直线 DE  直线 PA C．直线 DE  直线 AB D．直线 DE  直线 AC 8．已知平面 平面  ，交于直线l ，且直线 a  ，直线b  ，则下列命题错误的是（ ） A．若 / /a b ，则 / /a l 或 / /b l B．若 a b r r ，则 a l 且b l C．若直线 ,a b 都不平行直线l ，则直线 a 必不平行直线b D．若直线 ,a b 都不垂直直线l ，则直线 a 必不垂直直线b 9．以下四个命题中，正确的是（ ） A．若 1 1 2 3OP OA OB    ,则 , ,P A B 三点共线 B．若 , ,a b c   为空间的一个基底，则 , ,a b b c c a       构成空间的另一个基底 C．  a b c a b c        D． ABC 为直角三角形的充要条件是 · 0AB AC   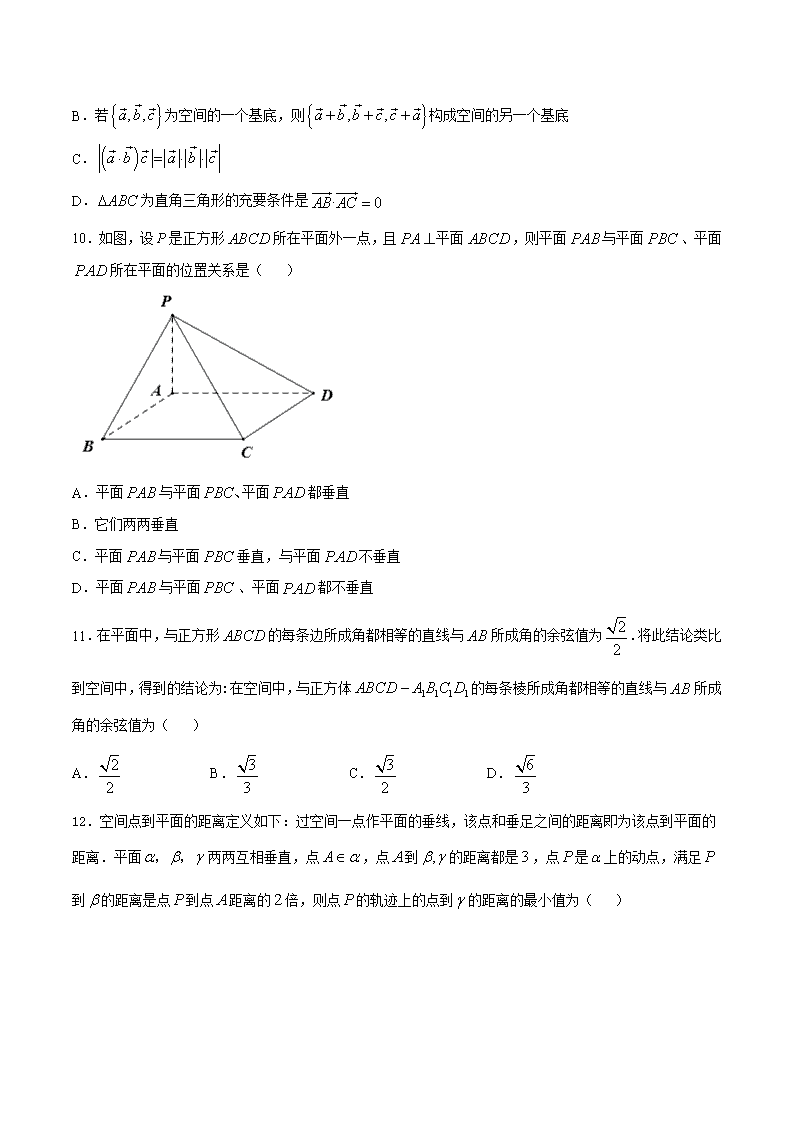10．如图，设 P 是正方形 ABCD 所在平面外一点，且 PA  平面 ABCD ，则平面 PAB 与平面 PBC 、平面 PAD 所在平面的位置关系是（ ） A．平面 PAB 与平面 PBC、平面 PAD 都垂直 B．它们两两垂直 C．平面 PAB 与平面 PBC 垂直，与平面 PAD 不垂直 D．平面 PAB 与平面 PBC 、平面 PAD 都不垂直 11．在平面中，与正方形 ABCD 的每条边所成角都相等的直线与 AB 所成角的余弦值为 2 2 .将此结论类比 到空间中，得到的结论为:在空间中，与正方体 1 1 1 1ABCD A B C D 的每条棱所成角都相等的直线与 AB 所成 角的余弦值为（ ） A． 2 2 B． 3 3 C． 3 2 D． 6 3 12．空间点到平面的距离定义如下：过空间一点作平面的垂线，该点和垂足之间的距离即为该点到平面的 距离．平面  ，， 两两互相垂直，点 A ，点 A到 , 的距离都是3 ，点 P是 上的动点，满足 P到  的距离是点 P到点 A距离的 2 倍，则点 P的轨迹上的点到 的距离的最小值为（ ） A． 3 B．3 2 3 C 6 3 D．3 3 二、填空题（共 20 分，每题 5 分） 13．如图，在下列四个正方体中， A 、 B 为正方体的两个顶点， , ,M N Q 为所在棱的中点，则在这四个正 方体中，直线 AB 与平面 MNQ 平行的是________. ① ② ③ ④． 14．图（1）为棱长为 1 的正方体，若正方体内有两个球相外切且又分别与正方体的三个面相切，则两球半 径之和为________. 15．正方体 1 1 1 1ABCDA B C D 的棱长为 1，在正方体内随机取点 M ，则使四棱锥 M ABCD 的体积小于 1 6 的 概率为__． 16．已知空间向量  2 1,3 ,0a x x  ，  1, , 3b y y  ，（其中 x 、y R ），如果存在实数  ，使得 a b  成立，则 x y  _____________. 三、解答题 17．（10 分）如图， ABCDFE 是由两个全等的菱形 ABEF 和CDFE 组成的空间图形， 2AB  ，∠BAF ＝∠ECD＝60°. （1）求证： BD DC ； （2）如果二面角 B－EF－D 的平面角为 60°，求直线 BD 与平面 BCE 所成角的正弦值. 18．（12 分）如图，在正方体 1 1 1 1ABCD A B C D 中，点 E ，F 分别在棱 1CC ，AB 上，且满足 12CE EC ， 2AF FB . （1）证明：平面 ADE  平面 1 1A D F ； （2）若 3AB  ，求平面 1 1AC F 截正方体 1 1 1 1ABCD A B C D 所得截面的面积. 19．（12 分）如图，在正方体 ABCD A B C D    中，O 是 A BD 的中心， ,E F 分别是线段 ,A C C D   上 的动点，且 A E A C    ，    1C F C D R      ． （Ⅰ）若直线 OE  平面 BC D ，求实数  的值； （Ⅱ）若 1 2   ，正方体 ABCD A B C D    的棱长为 2，求平面 BEF 和平面 A BD 所成二面角的余弦值． 20．（12 分）已知空间向量 1(sin , 1,cos ), (1,2cos ,1), , (0, )5 2a b a b          （1）求sin 2 及sin ,cos  的值； （2）设函数 ( ) 5cos(2 ) cos2 ( ), ( )f x x x x R f x    求 的最小正周期及 ( )f x 取得最大值时 x 的值。 21．（12 分）  ( 请用空间向量求解 ) 已知正四棱柱 1 1 1 1ABCD A B C D 中，AB 1 ， 1AA 3 ， ,E F 分别 是棱 1AA ， 1CC 上的点，且满足 1AE 2EA ， 1CF 2FC ．  1 求异面直线 1EC ， 1DB 所成角的余弦值；  2 求面 1 1EB C 与面 FAD 所成的锐二面角的余弦值． 22．（12 分）如图，三棱柱 1 1 1ABC A B C 中， 1AA  平面 ABC ， 90BAC   ， 2, 6AB AC  ,点 D 在线段 1BB 上，且 1 1 3BD BB , 1 1AC AC E . （1）试用空间向量证明直线 DE 与平面 ABC 不平行； （2）设平面 1ADC 与平面 ABC 所成的锐二面角为 ，若 7cos 7   ，求 1AA 的长； （3）在（2）的条件下，设平面 1ADC  平面 ABC l ，求直线l 与平面 1 1ABA B 的所成角.