2013届人教A版理科数学课时试题及解析（36）空间几何体的结构特征及三视图和直观图 7页

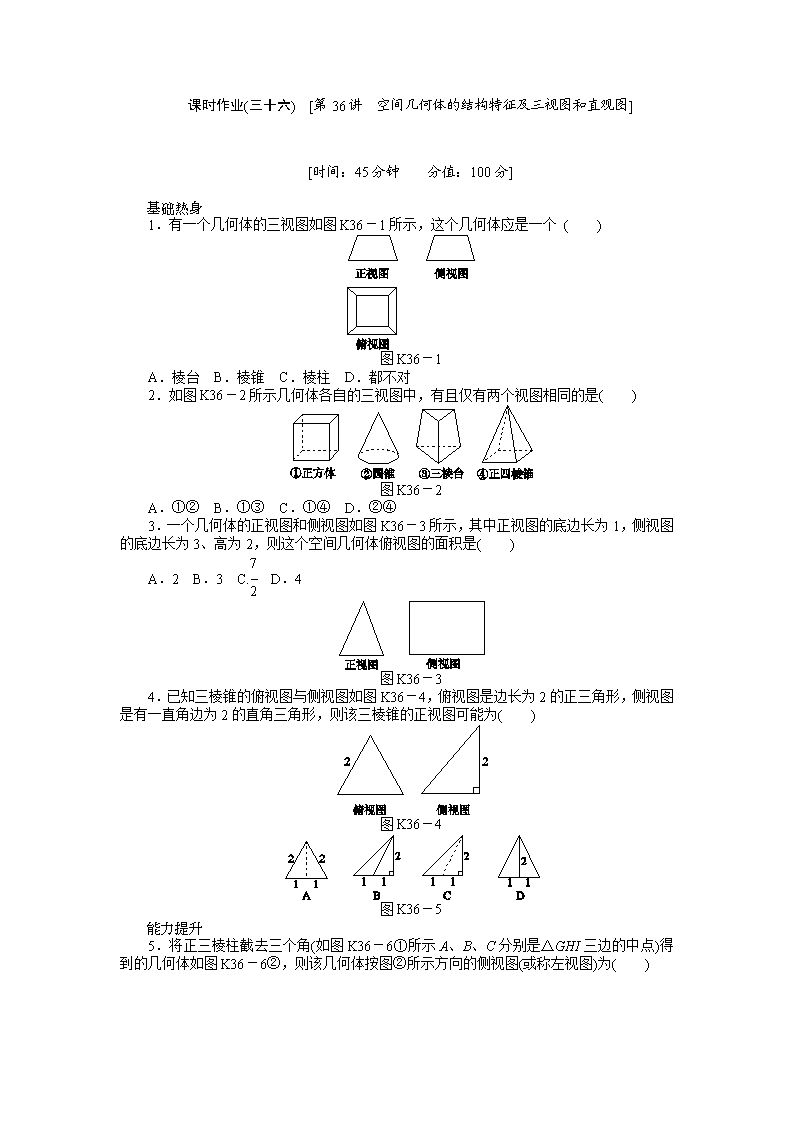
课时作业(三十六)　[第36讲　空间几何体的结构特征及三视图和直观图]‎ ‎[时间：45分钟　　分值：100分]‎ ‎1．有一个几何体的三视图如图K36－1所示，这个几何体应是一个 (　　)‎ 图K36－1‎ A．棱台 B．棱锥 C．棱柱 D．都不对 ‎2．如图K36－2所示几何体各自的三视图中，有且仅有两个视图相同的是(　　)‎ 图K36－2‎ A．①② B．①③ C．①④ D．②④‎ ‎3．一个几何体的正视图和侧视图如图K36－3所示，其中正视图的底边长为1，侧视图的底边长为3、高为2，则这个空间几何体俯视图的面积是(　　)‎ A．2 B．‎3 C. 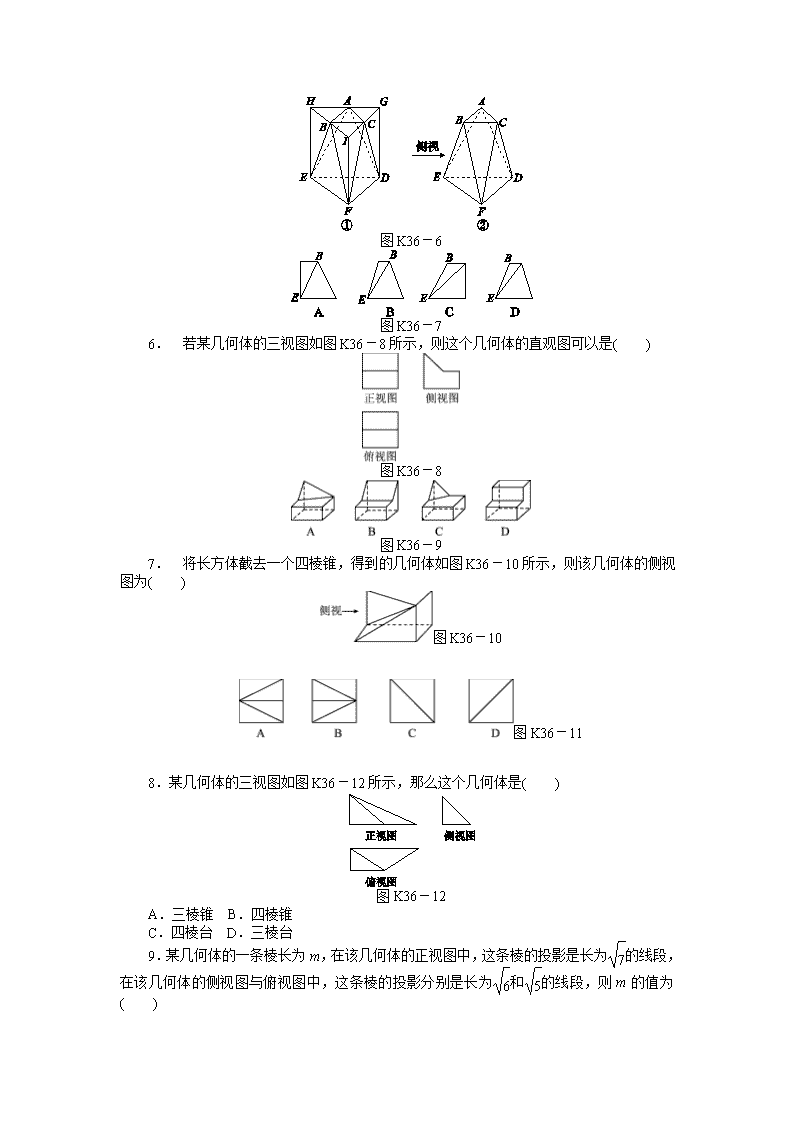D．4‎ 图K36－3‎ ‎4．已知三棱锥的俯视图与侧视图如图K36－4，俯视图是边长为2的正三角形，侧视图是有一直角边为2的直角三角形，则该三棱锥的正视图可能为(　　) ‎ 图K36－4‎ 图K36－5‎ ‎5．将正三棱柱截去三个角(如图K36－6①所示A、B、C分别是△GHI三边的中点)得到的几何体如图K36－6②，则该几何体按图②所示方向的侧视图(或称左视图)为(　　)‎ 图K36－6‎ 图K36－7‎ ‎6． 若某几何体的三视图如图K36－8所示，则这个几何体的直观图可以是(　　)‎ 图K36－8‎ 图K36－9‎ ‎7． 将长方体截去一个四棱锥，得到的几何体如图K36－10所示，则该几何体的侧视图为(　　)‎ 图K36－10‎ 图K36－11‎ ‎8．某几何体的三视图如图K36－12所示，那么这个几何体是(　　)‎ 图K36－12‎ A．三棱锥 B．四棱锥 C．四棱台 D．三棱台 ‎9．某几何体的一条棱长为m，在该几何体的正视图中，这条棱的投影是长为的线段，在该几何体的侧视图与俯视图中，这条棱的投影分别是长为和的线段，则m的值为(　　)‎ A．3 B．‎2 C．4 D．2 ‎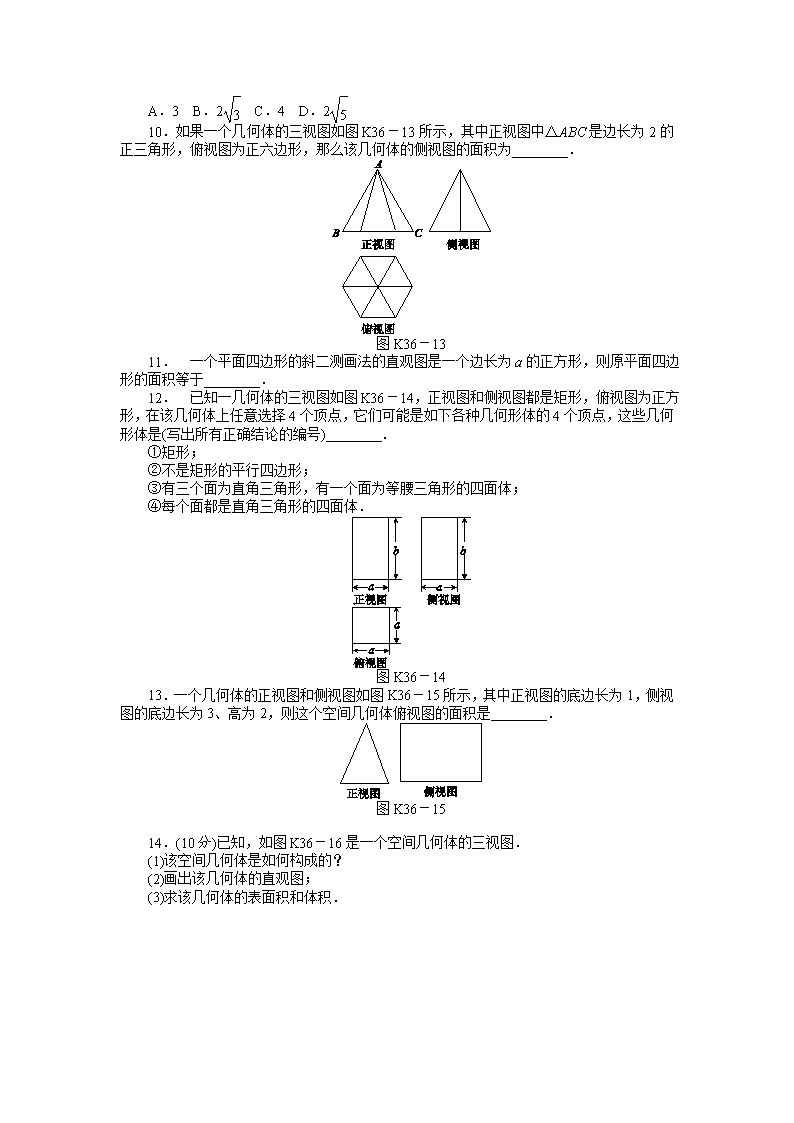10．如果一个几何体的三视图如图K36－13所示，其中正视图中△ABC是边长为2的正三角形，俯视图为正六边形，那么该几何体的侧视图的面积为________．‎ 图K36－13‎ ‎11． 一个平面四边形的斜二测画法的直观图是一个边长为a的正方形，则原平面四边形的面积等于________．‎ ‎12． 已知一几何体的三视图如图K36－14，正视图和侧视图都是矩形，俯视图为正方形，在该几何体上任意选择4个顶点，它们可能是如下各种几何形体的4个顶点，这些几何形体是(写出所有正确结论的编号)________．‎ ‎①矩形；‎ ‎②不是矩形的平行四边形；‎ ‎③有三个面为直角三角形，有一个面为等腰三角形的四面体；‎ ‎④每个面都是直角三角形的四面体．‎ 图K36－14‎ ‎13．一个几何体的正视图和侧视图如图K36－15所示，其中正视图的底边长为1，侧视图的底边长为3、高为2，则这个空间几何体俯视图的面积是________．‎ 图K36－15‎ ‎14．(10分)已知，如图K36－16是一个空间几何体的三视图．‎ ‎(1)该空间几何体是如何构成的？‎ ‎(2)画出该几何体的直观图；‎ ‎(3)求该几何体的表面积和体积．‎ 图K36－16‎ ‎15．(13分)有一块多边形菜地，它的水平放置的平面图形的斜二测直观图是直角梯形(如图K36－17所示)，∠A′B′C′＝45°，D′C′⊥A′D′，A′B′＝A′D′＝‎1 m，若平均每‎1 m2‎菜地所产生的经济效益是300元，则这块菜地所产生的总经济效益是多少元？(精确到1元)‎ 图K36－17‎ ‎16．(12分)一个几何体的三视图如图K36－18所示，其中正视图和侧视图是腰长为6的两个全等的等腰直角三角形．‎ ‎(1)请画出该几何体的直观图，并求出它的体积；‎ ‎(2)用多少个这样的几何体可以拼成一个棱长为6的正方体ABCD－A1B‎1C1D1? 如何组拼？试证明你的结论；‎ ‎(3)在(2)的情形下，设正方体ABCD－A1B‎1C1D1的棱CC1的中点为E, 求平面AB1E与平面ABC所成锐二面角的余弦值．‎ 图K36－18‎ 课时作业 (三十六)‎ ‎【基础热身】‎ ‎1．A　[解析] 根据三视图，这个空间几何体是棱台．‎ ‎2．D　[解析] 正方体的三个视图都相同，而三棱台的三个视图各不相同，正确答案为D.‎ ‎3．B　[解析] 这是一个将一个侧面水平放置的三棱柱，其俯视图如图，俯视图是一个边长分别为1,3的矩形，故其面积为3.‎ ‎4．C　[解析] 空间几何体的正视图和侧视图的“高平齐”，故正视图的高一定是2，正视图和俯视图“长对正”，故正视图的底面边长为2，根据侧视图中的直角说明这个空间几何体最前面的面垂直于底面，这个面遮住了后面的一个侧棱，综合这些可知，这个空间几何体的正视图可能是C.‎ ‎【能力提升】‎ ‎5．A　[解析] 截前的侧视图是一个矩形，截后改变的只是B，C，F方向上的．‎ ‎6．B　[解析] 由正视图可排除A，C；由侧视图可判断该几何体的直观图是B.‎ ‎7．D　[解析] 被截去的四棱锥的三条可见侧棱中有两条为正方体的面对角线，它们在右侧面上的投影与右侧面(正方形)的两条边重合，另一条为正方体的体对角线，它在右侧面上的投影与右侧面的对角线重合，对照各图及对角线方向，只有选项D符合．‎ ‎8．B　[解析] 由所给三视图与直观图的关系，可以判定对应的几何体为如图所示的四棱锥，且PA⊥面ABCD，AB⊥BC，BC∥AD.‎ ‎9．A　[解析] 结合长方体的对角线在三个面的投影来理解计算．‎ 如图，设长方体的长，宽，高分别为a，b，c，由题意得 ＝，＝，＝ ‎⇒a2＋b2＋c2＝9，所以对角线的长为＝3.‎ ‎∴选A.‎ ‎10.　[解析] 根据三视图的信息可以知道相应的空间几何体是一个正六棱锥，结合数据可知其底面正六边形的边长为1，棱锥的高为h＝.由于三视图中“宽相等”，那么侧视图中的三角形的底边边长与俯视图中正六边形的高相等，可得其长度为，则该几何体的侧视图的面积为S＝××＝. ‎ ‎11．‎2‎a2　[解析] 一个平面图形的面积S与它的直观图的面积S′之间的关系是S′＝S，而直观图面积S′＝a2.所以原平面四边形的面积为＝‎2‎a2.‎ ‎12．①③④　[解析] 如图所示长方体为几何体的直观图．‎ 当选择的四个点为A、B、C、D时，可知①正确；‎ 当选择B、A、B1、C时，可知③正确；‎ 当选择A、B、D、D1时，可知④正确．‎ ‎13．3　[解析] 这是一个将一个侧面水平放置的三棱柱，其俯视图如图．俯视图是一个边长分别为1,3的矩形，故其面积为3.‎ ‎14．[解答] (1)这个空间几何体的下半部分是一个底面各边长为2，高为1的长方体，上半部分是一个底面各边长为2，高为1的正四棱锥．‎ ‎(2)按照斜二测画法可以得到其直观图，如图．‎ ‎(3)由题意可知，该几何体是由长方体ABCD－A′B′C′D′与正四棱锥P－A′B′C′D′构成的简单几何体．‎ 由图易得：AB＝AD＝2，AA′＝1，PO′＝1，取A′B′中点Q，连接PQ，从而PQ＝＝＝，所以该几何体表面积 S＝(A′B′＋B′C′＋C′D′＋D′A′)PQ＋(A′B′＋B′C′＋C′D′＋D′A′)AA′＋AB·AD＝4＋12.‎ 体积V＝2×2×1＋×2×2×1＝.‎ ‎15．[解答] 在直观图中，过A′点作A′E⊥B′C′，垂足为E，则在Rt△A′B′E中，A′B′＝‎1 m，∠A′B′E＝45°，∴B′E＝ m.‎ 而四边形A′EC′D′为矩形，A′D′＝‎1 m，‎ ‎∴B′C′＝B′E＋EC′＝m.‎ 由此可还原图形，如图所示，在原图形中，AD＝‎1 m，AB＝‎2 m，BC＝m，且AD∥BC，AB⊥BC，‎ ‎∴这块菜地的面积为 S＝(AD＋BC)·AB＝×1＋1＋×2＝(m2)，‎ 所以这块菜地所产生的总的经济效益是300S≈300(2＋0.707)＝812.1≈812(元)．‎ ‎【难点突破】‎ ‎16．[解答] (1)该几何体的直观图如图(1)所示，它是有一条侧棱垂直于底面的四棱锥. 其中底面ABCD是边长为6的正方形，高为CC1＝6，故所求体积是V＝×62×6＝72.‎ ‎(2)依题意，正方体的体积是原四棱锥体积的3倍，故用3个这样的四棱锥可以拼成一个棱长为6的正方体，‎ 其拼法如图(2)所示. ‎ 证明：∵面ABCD、面ABB‎1A1、面AA1D1D为全等的正方形，于是 VC1－ABCD＝VC1－ABB‎1A1＝VC1－AA1D1D，故所拼图形成立．‎ ‎(3)设B1E，BC的延长线交于点G，连接GA，在底面ABC内作BH⊥AG，垂足为H，连接HB1，如图(2)，则B1H⊥AG，故∠B1HB为平面AB1E与平面ABC所成锐二面角或其补角的平面角. ‎ 在Rt△ABG中，AG＝，则BH＝＝，B1H ＝ ＝ ，‎ cos∠B1HB＝＝.‎ 故平面AB1E与平面ABC所成锐二面角的余弦值为.‎ ‎ ‎