人教A高中数学必修三 系统抽样目标导学 5页

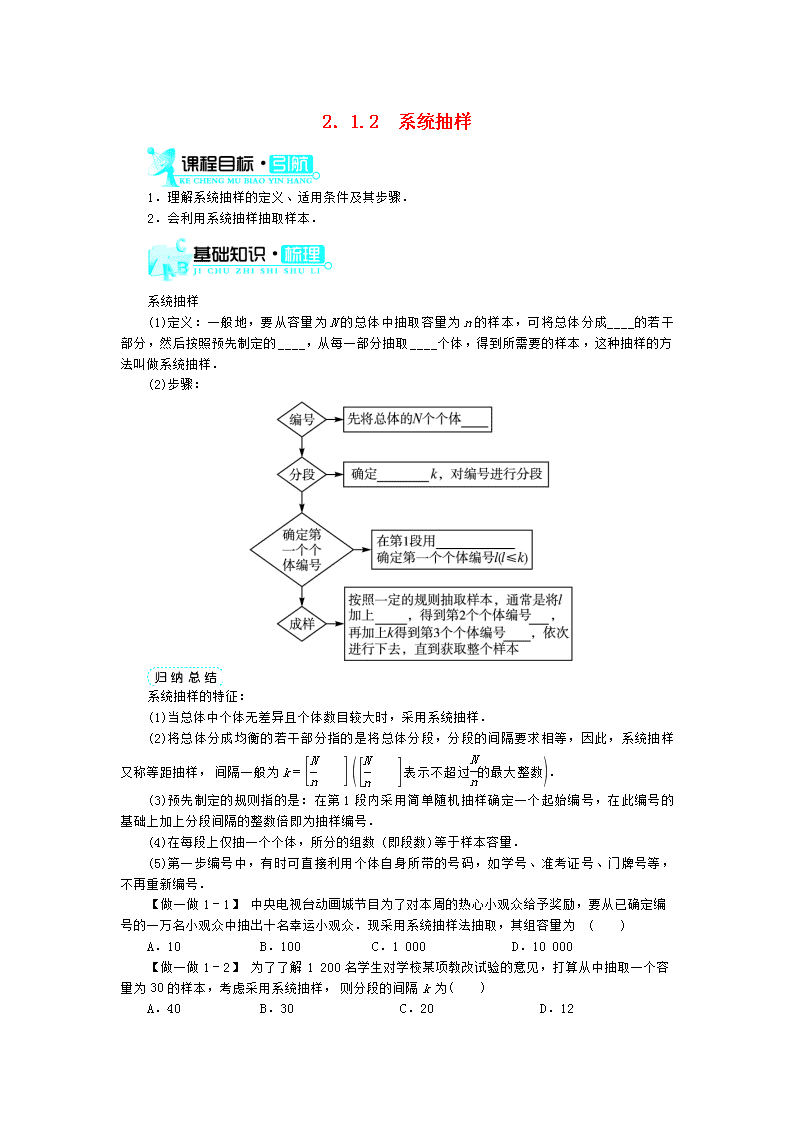
‎2．1.2　系统抽样 ‎1．理解系统抽样的定义、适用条件及其步骤．‎ ‎2．会利用系统抽样抽取样本．‎ 系统抽样 ‎(1)定义：一般地，要从容量为N的总体中抽取容量为n的样本，可将总体分成____的若干部分，然后按照预先制定的____，从每一部分抽取____个体，得到所需要的样本，这种抽样的方法叫做系统抽样．‎ ‎(2)步骤：‎ 系统抽样的特征：‎ ‎(1)当总体中个体无差异且个体数目较大时，采用系统抽样．‎ ‎(2)将总体分成均衡的若干部分指的是将总体分段，分段的间隔要求相等，因此，系统抽样又称等距抽样，间隔一般为k＝.‎ ‎(3)预先制定的规则指的是：在第1段内采用简单随机抽样确定一个起始编号，在此编号的基础上加上分段间隔的整数倍即为抽样编号．‎ ‎(4)在每段上仅抽一个个体，所分的组数(即段数)等于样本容量．‎ ‎(5)第一步编号中，有时可直接利用个体自身所带的号码，如学号、准考证号、门牌号等，不再重新编号．‎ ‎【做一做1－1】 中央电视台动画城节目为了对本周的热心小观众给予奖励，要从已确定编号的一万名小观众中抽出十名幸运小观众．现采用系统抽样法抽取，其组容量为(　　)‎ A．10 B．‎100 ‎ C．1 000 D．10 000‎ ‎【做一做1－2】 为了了解1 200名学生对学校某项教改试验的意见，打算从中抽取一个容量为30的样本，考虑采用系统抽样，则分段的间隔k为(　　)‎ A．40 B．‎30 ‎ C．20 D．12‎ 答案：(1)均衡　规则　一个　(2)编号　分段间隔　简单随机抽样　间隔k　l＋k　l＋2k ‎【做一做1－1】 C　依题意，要抽十名幸运小观众，所以要分成十个组，每个组容量为10 000÷10＝1 000，即分段间隔．‎ ‎【做一做1－2】 A　∵N＝1 200，n＝30，∴k＝＝＝40.‎ ‎1．系统抽样与简单随机抽样的区别 剖析：(1)系统抽样比简单随机抽样更容易实施，可节约抽样成本．‎ ‎(2)抽样所得样本的代表性与具体的编号有关，而简单随机抽样所得样本的代表性与个体的编号无关．如果编号的个体特征随编号的变化呈现一定的周期性，则可能会使抽样的代表性差些．‎ ‎(3)系统抽样的应用比简单随机抽样的应用更广泛，尤其是工业生产线上对产品质量的检验，由于不知道产品的数量，因此不能用简单随机抽样．‎ ‎2．系统抽样与简单随机抽样的联系 剖析：(1)对总体均分后的每一部分进行抽样时，采用的是简单随机抽样．‎ ‎(2)与简单随机抽样一样，系统抽样是等概率抽样，它是客观的、公平的．‎ ‎(3)与简单随机抽样一样是不放回抽样．‎ ‎(4)总体中的个体数恰好能被样本容量整除时，可用它们的比值作为系统抽样的间隔；当总体中的个体数不能被样本容量整除时，可用简单随机抽样先从总体中剔除少量个体，使剩下的个体数能被样本容量整除后再进行系统抽样．‎ ‎3．系统抽样中的合理分段问题 剖析：系统抽样操作的要领是先将个体数较多的总体分成均衡的若干部分，然后按照预先制定的规则，从每一部分中抽取1个个体，从而得到所需的样本．由于抽样的间隔相等，因此系统抽样又称为等距抽样(或叫机械抽样)，所以系统抽样中必须对总体中的每个个体进行合理(即等距)分段．‎ ‎(1)若从容量为N的总体中抽取容量为n的样本，用系统抽样时，应先将总体中的各个个体编号，再确定分段间隔k，以便对总体进行分段．‎ ‎(2)当是整数时，取k＝作为分段间隔即可，如N＝100，n＝20，则分段间隔k＝＝5.也就是将100个个体按平均每5个为1段(组)进行分段(组)；‎ ‎(3)当不是整数时，应先从总体中随机剔除一些个体，使剩余个体数N′能被n整除，这时分段间隔k＝，如N＝101，n＝20，则应先用简单随机抽样从总体中剔除1个个体，使剩余的总体容量(即100)能被20整除，从而得出分段间隔k＝＝5，也就是说，只需将100个个体平均分为20段(组)．‎ ‎(4)一般地，用简单随机抽样的方法从总体中剔除部分个体，其个数为总体中的个体数除以样本容量所得的余数．‎ 题型一 如何选择系统抽样 ‎【例题1】 下列问题中，最适合用系统抽样抽取样本的是(　　)‎ A．从10名学生中，随机抽取2名学生参加义务劳动 B．从全校3 000名学生中，随机抽取100名学生参加义务劳动 C．从某市30 000名学生中，其中小学生有14 000人，初中生有10 000人，高中生有6 000人，抽取300名学生以了解该市学生的近视情况 D．从某班周二值日小组6人中，随机抽取1人擦黑板 反思：如果总体中个体满足下列条件，那么可用系统抽样抽取样本：‎ ‎①总体中个体之间无差异；‎ ‎②总体中个体数较多．‎ 题型二 系统抽样的应用 ‎【例题2】 某校高中三年级的295名学生已经编号为1,2，…，295，为了了解学生的学习情况，要按1∶5的比例抽取一个样本．请用系统抽样的方法进行抽取，并写出过程．‎ 分析：按1∶5的比例确定样本容量，再按系统抽样的步骤进行，关键是确定第1段的编号．‎ 反思：利用系统抽样抽取样本时，要注意在每一段上仅抽取一个个体，并且抽取出的个体编号按从小到大顺序排列时，从第2个号码起，每个号码与前面一个号码的差都等于同一个常数，这个常数就是分段间隔，因此系统抽样又称为等距抽样．‎ 题型三 易错辨析 ‎【例题3】 现从全班63人中，用系统抽样方法任选10人进行高中生体重与身高的关系的调查．应如何实施？‎ 错解：由于不是整数，‎ 因此先用简单抽样方法从总体中随机剔除3个个体，然后分段间隔为＝6.‎ 第一步，先将63人编号，号码是01,02，…，63；‎ 第二步，随机剔除3人；‎ 第三步，将余下的60人，按照男女生交替排成一路纵队，用掷骰子的方法在前6名中任选1名，对应号码为l；‎ 第四步，将队中序列号为l，l＋6，l＋6×2，…，l＋6×9的10名同学选出来，组成容量为10的样本．‎ 错因分析：由于男女生交替排列，因而单、双号分别对应男生或女生，因此如果从第一段中抽出一个个体号l(假如是男生)，则后面所取个体都是男生．由于男生和女生的体重分布有明显的不同，则抽取的样本仅仅代表了某一性别的个体，因此这个样本不具有代表性．‎ 答案：‎ ‎【例题1】 B　A项中总体个体无差异，但个数较少，适合用简单随机抽样；同样D项中也适合用简单随机抽样；C项中总体中个体有差异不适合用系统抽样；B项中，总体中有3 000个个体，个数较多且无差异，适合用系统抽样．‎ ‎【例题2】 解：按照1∶5的比例抽取样本，则样本容量为×295＝59.‎ 抽样步骤是：‎ ‎(1)编号：按现有的号码．‎ ‎(2)确定分段间隔k＝5，把295名同学分成59组，每组5人；第1段 是编号为1～5的5名学生，第2段是编号为6～10的5名学生，依次下去，第59段是编号为291～295的5名学生．‎ ‎(3)采用简单随机抽样的方法，从第一段5名学生中抽出一名学生，不妨设编号为l(1≤l≤5)．‎ ‎(4)那么抽取的学生编号为l＋5k(k＝0,1,2，…，58)，得到59个个体作为样本，如当l＝3时的样本编号为3,8,13，…，288,293.‎ ‎【例题3】 正解：第一步，先对63人随机编号01,02，…，63；‎ 第二步，用抽签法从63人中随机剔除3人；‎ 第三步，余下60人重新编号为01,02,03，…，60，并分成10段，每段6人；‎ 第四步，从第一段6人中用抽签法抽出1个号，如02；‎ 第五步，将号码为02,08,14,20,26,32,38,44,50,56的学生作为样本．‎ ‎1．为了了解参加一次知识竞赛的1 252名学生的成绩，决定采用系统抽样的方法抽取一个容量为50的样本．那么总体中应随机剔除的个体数目是(　　)‎ A．2 B．‎4 ‎ C．5 D．6‎ ‎2．某中学从已编号(1～60)的60个班级中，随机抽取6个班级进行卫生检查，用每部分选取的号码间隔一样的系统抽样方法确定所选的6个班级的编号可能是(　　)‎ A．6,16,26,36,46,56 B．3,10,17,24,31,38‎ C．4,11,18,25,32,39 D．5,14,23,32,41,50‎ ‎3．下列抽样试验中，最适宜用系统抽样法的是(　　)‎ A．某市的4个区共有2 000名学生，4个区的学生人数之比为3∶2∶8∶2，从中抽取200人入样 B．从某厂生产的2 000个电子元件中抽取50个入样 C．从某厂生产的10个电子元件中抽取2个入样 D．从某厂生产的20个电子元件中抽取5个入样 ‎4．将参加数学竞赛的1 000名学生编号如下000,001,002，…，999，打算从中抽取一个容量为50的样本，按系统抽样方法分成50个部分，第一段编号为000,002，…，019，如果在第一段随机抽取的一个号码为015，则抽取的第40个号码为__________．‎ ‎5．某单位的在岗职工为620人，为了调查上班时，从家到单位的路上平均所用的时间，决定抽取10%的职工调查这一情况，如何采用系统抽样抽取样本？‎ 答案：1．A　因为1 252＝50×25＋2，所以应随机剔除2个个体．‎ ‎2．A　选取的号码间隔一样的系统抽样方法，需把总体分为6段，即1～10,11～20,21～30,31～40,41～50,51～60，既符合间隔为10又符合每一段取一号的只有A项．‎ ‎3．B　A项中总体中个体间有差异，不适用系统抽样；C项和D项中总体中个体无差异，但个体数目不多，不适用系统抽样；B项中总体中个体间无差异，且个体数目较多，适宜用系统抽样．‎ ‎4．795　利用系统抽样抽取样本，在第1段抽取号码为015，分段间隔为＝20，则在第i段中抽取号码为015＋20(i－1)．则抽取的第40个号码为015＋(40－1)×20＝795.‎ ‎5．解：用系统抽样抽取样本，样本容量是620×10%＝62.‎ 步骤是：‎ ‎(1)编号：把这620人随机编号为1,2,3，…，620.‎ ‎(2)确定分段间隔k＝＝10，把620人分成62段，每段10人；第1段是编号为1～10的10人，第2段是编号为11～20的10人，依次下去，第62段是编号为611～620的10人．‎ ‎(3)采用简单随机抽样的方法，从第1段10人中抽出一人，不妨设编号为l(1≤l≤10)．‎ ‎(4)那么抽取的职工编号为l＋10k(k＝0,1,2，…，61)，得到62个个体作为样本，如当l＝3时的样本编号为3,13,23，…，603,613.‎