- 1.24 MB
- 2021-06-30 发布
- 1、本文档由用户上传,淘文库整理发布,可阅读全部内容。
- 2、本文档内容版权归属内容提供方,所产生的收益全部归内容提供方所有。如果您对本文有版权争议,请立即联系网站客服。
- 3、本文档由用户上传,本站不保证质量和数量令人满意,可能有诸多瑕疵,付费之前,请仔细阅读内容确认后进行付费下载。
- 网站客服QQ:403074932
第
3
课时
题型
1
利用空间向量求空间角
(
距离
)
就新课标卷而言,对立体几何的命题基本上是“一题两
法”的格局
.
在备考中,对理科考生而言,还是应该注重两种方
法并重,不要盲
目地追求空间向量
(
容易建系时才用空间向量
)
,
千万不要重计算而轻论证!
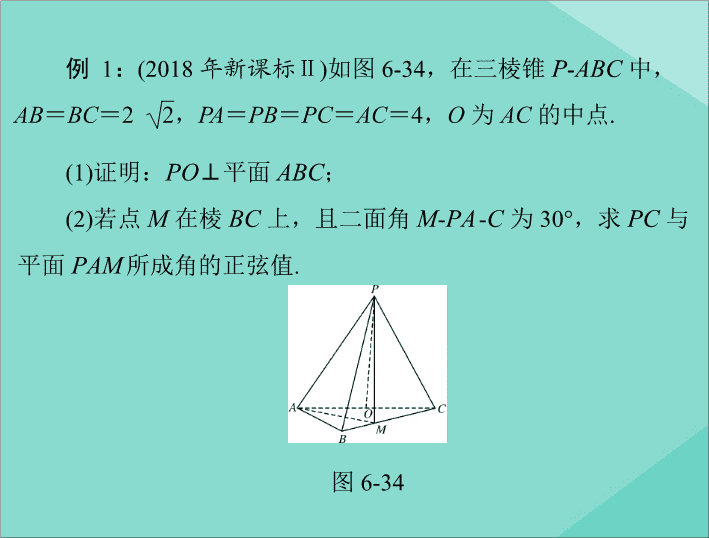
例
1
:
(20
18
年新课标
Ⅱ
)
如图
6-34
,在三棱锥
P
-
ABC
中,
(1)
证明:
PO
⊥
平面
ABC
;
(2)
若点
M
在棱
BC
上,且二面角
M
-
PA
-
C
为
30°
,求
PC
与
平面
PAM
所成角的正弦值
.
图
6-34
图
6-35
【
规律方法
】
立体几何中的直线与平面的位置关系,以及
空间的三种角,是高考的必考内容,都可以采用传统的方法来
处理,对于直线与平面间几种位置关系,可采用平行垂直间的
转化关系来证明,对于异面直线所成的角、直线与平面所成的
角和二面角可分别通过平移法、射影法和垂面法将它们转化为
相交直线所成的角来处理
.
本题主要考查立体几何中传统的平
行与垂直关系,并且考查了线面所成的角,难度并不是太大,
旨在考查考生对解题技巧的把握和抽象分析能力
.
【
跟踪训练
】
1.(2017
年新课标
Ⅰ
)
如图
6-36
,在四棱锥
P
-
ABCD
中,
AB
∥
CD
,且
∠
BAP
=
∠
CDP
=
90°.
(1)
证明:平面
PAB
⊥
平面
PAD
;
(2)
若
PA
=
PD
=
AB
=
DC
,
∠
APD
=
90°
,求二面角
A
-
PB
-
C
的余弦值
.
图
6-36
(1)
证明:
由已知
∠
BAP
=
∠
CDP
=
90°
,得
AB
⊥
AP
,
CD
⊥
PD
.
由于
AB
∥
CD
,故
AB
⊥
PD
.
又
AP
∩
PD
=
P
,从而
AB
⊥
平面
PAD
.
又
AB
⊂
平面
PAB
,
∴
平面
PAB
⊥
平面
PAD
.
(2)
解:
在平面
PAD
内作
PF
⊥
AD
,垂足为
F
,
由
(1)
可知,
AB
⊥
平面
PAD
,故
AB
⊥
PF
,可得
PF
⊥
平面
ABCD
.
.
图
D101
题型
2
折叠问
题
将平面图形沿其中一条或几条线段折起,使其成为空间图
形,把这类问题称为平面图形的翻折问题
.
平面图形经过翻折成
为空间图形后,原有的性质有的发生了变化,有的没有发生变
化,弄清
它们是解决问题的关键
.
一般地,翻折后还在同一个平
面上的性质不发生变化,不在同一个平面上的性质发生变化
.
解
决这类问题就是要据此研究翻折以后的空间图形中的线面关系
和几何量的度量值
,这是化解翻折问题难点的主要方法
.
例
2
:
(20
18
年新课标
Ⅰ
)
如图
6-37
,四边形
ABCD
为正方
形,
E
,
F
分别为
AD
,
BC
的中点,以
DF
为折痕把
△
DFC
折
起,使点
C
到达点
P
的位置,且
PF
⊥
BF
.
(1)
证明:平面
PEF
⊥
平面
ABFD
;
(2)
求
DP
与平面
ABFD
所成角的正弦值
.
图
6-37
(1)
证明:
由已知可得,
BF
⊥
PF
,
BF
⊥
EF
,
又
PF
∩
EF
=
F
,
∴
BF
⊥
平面
PEF
.
又
BF
⊂
平面
ABFD
,
∴
平面
PEF
⊥
平面
ABFD
.
(2)
解:
作
PH
⊥
EF
,垂足为
H
.
由
(1)
得,
PH
⊥
平面
ABFD
.
建立如图
6-38
所示的空间直角坐标系
H
-
xyz
.
图
6-38
【
规律方法
】
有关折叠问题,一定要分清折叠前后两图形
(
折叠前的平面图形和折叠后的空间图形
)
各元素间的位置和数
量关系,哪些变,哪些不变
.
如角的大小不变,线段长度不变,
线线关系不变,再由面面垂直的判定定理进行推理证明
.
【
跟踪训练
】
2.
如图
6-39
,在四边形
ABED
中,
AB
∥
DE
,
AB
⊥
BE
,点
C
在
AB
上,且
AB
⊥
CD
,
AC
=
BC
=
CD
= ,现将
2
ACD
沿
CD
折起,使点
A
到达点
P
的位置,且
PE
与平面
PBC
所成的角为
45°.
(1)
求证:平面
PBC
⊥
平面
DEBC
;
(2)
求二面角
D
-
PE
-
B
的余弦值
.
图
6-39
(1)
证明:
∵
AB
⊥
CD
,
AB
⊥
BE
,
∴
CD
∥
EB
.
∵
AC
⊥
CD
,
∴
PC
⊥
CD
.∴
EB
⊥
PC
,
且
PC
∩
BC
=
C
,
∴
EB
⊥
平面
PBC,
又
∵
EB
⊂
平面
DEBC
,
∴
平面
PBC
⊥
平面
DEBC
.
图
D102
(2)
解:
由
(1
)
知
EB
⊥
平面
PBC
,
∴
EB
⊥
PB
,
由
PE
与平面
PBC
所成的角为
45°
,得
∠
EPB
=
45°
,
∴△
PBE
为等腰直角三角形,
∴
PB
=
BE
.
∵
AB
∥
DE
,结合
CD
∥
EB
得
BE
=
CD
=
2
,
∴
PB
= ,故
2
PBC
为等边三角形
.
取
BC
的中点
O
,连接
PO
,
∵
PO
⊥
BC
,
∴
PO
⊥
平面
EBCD
,
以
O
为坐标原点,过点
O
与
BE
平行的直线为
x
轴,
CB
所在的直线为
y
轴,
OP
所在的直线为
z
轴建立空间直角坐标系
如图
D102
,
题型
3
探索性问题
图
6-40
(1)
证明:
连接
AC
,如图
6-41.
∴
BC
2
=
AB
2
+
AC
2
,
∴
AB
⊥
AC
.
∵
AB
∥
CD
,
∴
AC
⊥
CD
.
又
∵
PA
⊥
底面
ABCD,
∴
PA
⊥
CD
.
∵
AC
∩
PA
=
A
,
∴
CD
⊥
平面
PAC
.
图
6-41
(2)
解:
如图
6-41
,以
A
为原点,
AB
,
AC
,
AP
所在直线分
别为
x
,
y
,
z
轴建立空间直角坐标系,则
A
(0,0,0)
,
P
(0,0,2)
,
B
(2,0,0)
,
C
(0,2,0)
,
D
(
-
2,2,0).
∵
M
是棱
PD
的中点,
∴
M
(
-
1,1,1).
【
跟踪训练
】
3.
如图
6-42
,
ABEDFC
为多面体,平面
ABED
与平面
ACFD
垂直,点
O
在线段
AD
上,
OA
=
1
,
OD
= ,
2
OAB
,
△
OAC
,
△
ODE
,
△
ODF
都是正三角形
.
(1)
证明:直线
BC
∥
面
OEF
;
(2)
在线段
DF
上是否存在一点
M
,使得二面角
M
-
OE
-
D
的
在的位置
.
图
6-42
(1)
证明:
依题意,在平面
AD
FC
中,
∠
CAO
=
∠
FOD
=
60°
,
∴
AC
∥
OF
.
又
OF
⊂
平面
OEF
,
∴
AC
∥
平面
OEF
.
①
同理,在平面
ABED
中,
∠
BAO
=
∠
EOD
=
60°
,
∴
AB
∥
OE
,
∴
AB
∥
平面
OEF
.
②
∵
AB
∩
AC
=
A
,
OE
∩
OF
=
O
,
AB
∥
面
OEF
,
AC
∥
面
OEF
,
OE
⊂
面
OEF
,
OF
⊂
面
OEF
,
由
①②
可得,平面
ABC
∥
平面
OEF
.
又
BC
⊂
面
ABC
,
∴
直线
BC
∥
面
OEF
.
(
本题可先证明
BC
∥
EF
后得证,也可建立空间直
角坐标系
得证
)
相关文档
- 2021高考数学大一轮复习单元质检八2021-06-3010页
- 2020_2021学年新教材高中数学第八2021-06-3030页
- 2013-2017高考数学分类汇编-第8章 2021-06-3012页
- 2014高考数学题库精选核心考点大冲2021-06-3060页
- 2019届二轮复习高考解答题突破(四)2021-06-2527页
- 2019届二轮复习(理)第八章立体几何与2021-06-2542页
- 2018届二轮复习立体几何中的向量方2021-06-2539页
- 2021版高考数学一轮复习第8章立体2021-06-2577页
- 广东省2013届高三数学理科试题精选2021-06-2534页
- 高考数学复习专题练习第7讲 立体2021-06-258页