2015年湖北省高考数学试卷（理科） 32页

‎2015年湖北省高考数学试卷（理科）‎ ‎　‎ 一、选择题：本大题共10小题，每小题5分，共50分.在每小题给出的四个选项中，只有一项是符合题目要求的.‎ ‎1．（5分）i为虚数单位，i607的共轭复数为（　　）‎ A．i B．﹣i C．1 D．﹣1‎ ‎2．（5分）我国古代数学名著《九章算术》有“米谷粒分”题：粮仓开仓收粮，有人送来米1534石，验得米内夹谷，抽样取米一把，数得254粒内夹谷28粒，则这批米内夹谷约为（　　）‎ A．134石 B．169石 C．338石 D．1365石 ‎3．（5分）已知（1+x）n的展开式中第4项与第8项的二项式系数相等，则奇数项的二项式系数和为（　　）‎ A．212 B．211 C．210 D．29‎ ‎4．（5分）设X～N（μ1，σ12），Y～N（μ2，σ22），这两个正态分布密度曲线如图所示．下列结论中正确的是（　　）‎ A．P（Y≥μ2）≥P（Y≥μ1） B．P（X≤σ2）≤P（X≤σ1）‎ C．对任意正数t，P（X≤t）≥P（Y≤t） D．对任意正数t，P（X≥t）≥P（Y≥t）‎ ‎5．（5分）设a1，a2，…，an∈R，n≥3．若p：a1，a2，…，an成等比数列；q：（a12+a22+…+an﹣12）（a22+a32+…+an2）=（a1a2+a2a3+…+an﹣1an）2，则（　　）‎ A．p是q的充分条件，但不是q的必要条件 B．p是q的必要条件，但不是q的充分条件 C．p是q的充分必要条件 D．p既不是q的充分条件，也不是q的必要条件 ‎6．（5分）已知符号函数sgnx=，f（x）是R上的增函数，g（x）=f（x）﹣f（ax）（a＞1），则（　　）‎ A．sgn[g（x）]=sgnx B．sgn[g（x）]=﹣sgnx C．sgn[g（x）]=sgn[f（x）] D．sgn[g（x）]=﹣sgn[f（x）]‎ ‎7．（5分）在区间[0，1]上随机取两个数x，y，记P1为事件“x+y≥”的概率，P2为事件“|x﹣y|≤”的概率，P3为事件“xy≤”的概率，则（　　）‎ A．P1＜P2＜P3 B．P2＜P3＜P1 C．P3＜P1＜P2 D．P3＜P2＜P1‎ ‎8．（5分）将离心率为e1的双曲线C1的实半轴长a和虚半轴长b（a≠b）同时增加m（m＞0）个单位长度，得到离心率为e2的双曲线C2，则（　　）‎ A．对任意的a，b，e1＞e2‎ B．当a＞b时，e1＞e2；当a＜b时，e1＜e2‎ C．对任意的a，b，e1＜e2‎ D．当a＞b时，e1＜e2；当a＜b时，e1＞e2‎ ‎9．（5分）已知集合A={（x，y）|x2+y2≤1，x，y∈Z}，B={（x，y）||x|≤2，|y|≤2，x，y∈Z}，定义集合A⊕B={（x1+x2，y1+y2）|（x1，y1）∈A，（x2，y2）∈B}，则A⊕B中元素的个数为（　　）‎ A．77 B．49 C．45 D．30‎ ‎10．（5分）设x∈R，[x]表示不超过x的最大整数．若存在实数t，使得[t]=1，[t2]=2，…，[tn]=n同时成立，则正整数n的最大值是（　　）‎ A．3 B．4 C．5 D．6‎ ‎　‎ 二、填空题：本大题共4小题，考生需作答5小题，每小题5分，共25分．请将答案填在答题卡对应题号的位置上．答错位置，书写不清，模棱两可均不得分．‎ ‎11．（5分）已知向量⊥，||=3，则•=　　．‎ ‎12．（5分）函数f（x）=4cos2cos（﹣x）﹣2sinx﹣|ln（x+1）|的零点个数为　　．‎ ‎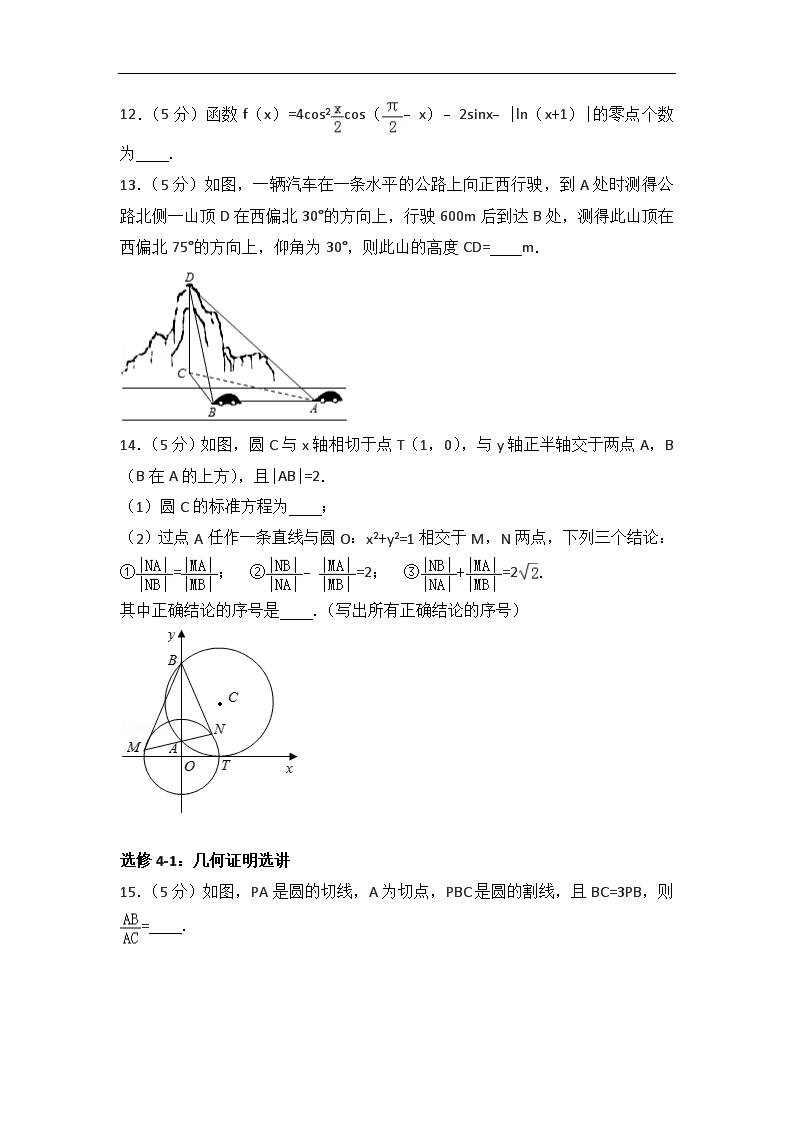13．（5分）如图，一辆汽车在一条水平的公路上向正西行驶，到A处时测得公路北侧一山顶D在西偏北30°的方向上，行驶600m后到达B处，测得此山顶在西偏北75°的方向上，仰角为30°，则此山的高度CD=　　m．‎ ‎14．（5分）如图，圆C与x轴相切于点T（1，0），与y轴正半轴交于两点A，B（B在A的上方），且|AB|=2．‎ ‎（1）圆C的标准方程为　　；‎ ‎（2）过点A任作一条直线与圆O：x2+y2=1相交于M，N两点，下列三个结论：‎ ‎①=； ②﹣=2； ③+=2．‎ 其中正确结论的序号是　　．（写出所有正确结论的序号）‎ ‎　‎ 选修4-1：几何证明选讲 ‎15．（5分）如图，PA是圆的切线，A为切点，PBC是圆的割线，且BC=3PB，则=　　．‎ ‎　‎ 选修4-4：坐标系与参数方程 ‎16．在直角坐标系xOy中，以O为极点，x轴的正半轴为极轴建立极坐标系．已知直线l的极坐标方程为ρ（sinθ﹣3cosθ）=0，曲线C的参数方程为（ t为参数），l与C相交于A，B两点，则|AB|=　　．‎ ‎　‎ 三、解答题：本大题共6小题，共75分．解答应写出文字说明、证明过程或演算步骤．‎ ‎17．（11分）某同学用“五点法”画函数f（x）=Asin（ωx+φ）（ω＞0，|φ|＜）在某一个周期内的图象时，列表并填入了部分数据，如表：‎ ωx+φ ‎0‎ π ‎2π x Asin（ωx+φ）‎ ‎0‎ ‎5‎ ‎﹣5‎ ‎0‎ ‎（1）请将上表数据补充完整，填写在相应位置，并直接写出函数f（x）的解析式；‎ ‎（2）将y=f（x）图象上所有点向左平行移动θ（θ＞0）个单位长度，得到y=g（x）的图象．若y=g（x）图象的一个对称中心为（，0），求θ的最小值．‎ ‎18．（12分）设等差数列{an}的公差为d，前n项和为Sn，等比数列{bn}的公比为q，已知b1=a1，b2=2，q=d，S10=100．‎ ‎（1）求数列{an}，{bn}的通项公式 ‎（2）当d＞1时，记cn=，求数列{cn}的前n项和Tn．‎ ‎19．（12分）《九章算术》中，将底面为长方形且有一条侧棱与底面垂直的四棱锥称之为阳马，将四个面都为直角三角形的四面体称之为鳖臑．如图，在阳马P﹣ABCD中，侧棱PD⊥底面ABCD，且PD=CD，过棱PC的中点E，作EF⊥PB交PB于点F，连接DE，DF，BD，BE．‎ ‎（1）证明：PB⊥平面DEF．试判断四面体DBEF是否为鳖臑，若是，写出其每个面的直角（只需写出结论）；若不是，说明理由；‎ ‎（2）若面DEF与面ABCD所成二面角的大小为，求的值．‎ ‎20．（12分）某厂用鲜牛奶在某台设备上生产A，B两种奶制品．生产1吨A产品需鲜牛奶2吨，使用设备1小时，获利1000元；生产1吨B产品需鲜牛奶1.5吨，使用设备1.5小时，获利1200元．要求每天B产品的产量不超过A产品产量的2倍，设备每天生产A，B两种产品时间之和不超过12小时．假定每天可获取的鲜牛奶数量W（单位：吨）是一个随机变量，其分布列为 W ‎12‎ ‎15‎ ‎18‎ P ‎0.3‎ ‎0.5‎ ‎0.2‎ 该厂每天根据获取的鲜牛奶数量安排生产，使其获利最大，因此每天的最大获利Z（单位：元）是一个随机变量．‎ ‎（1）求Z的分布列和均值；‎ ‎（2）若每天可获取的鲜牛奶数量相互独立，求3天中至少有1天的最大获利超过10000元的概率．‎ ‎21．（14分）一种画椭圆的工具如图1所示．O是滑槽AB的中点，短杆ON可绕O转动，长杆MN通过N处铰链与ON连接，MN上的栓子D可沿滑槽AB滑动，且DN=ON=1，MN=3，当栓子D在滑槽AB内作往复运动时，带动N绕O转动，M处的笔尖画出的椭圆记为C，以O为原点，AB所在的直线为x轴建立如图2所示的平面直角坐标系．‎ ‎（1）求椭圆C的方程；‎ ‎（2）设动直线l与两定直线l1：x﹣2y=0和l2：x+2y=0分别交于P，Q两点．若直线l总与椭圆C有且只有一个公共点，试探究：△OPQ的面积是否存在最小值？若存在，求出该最小值；若不存在，说明理由．‎ ‎22．（14分）已知数列{an}的各项均为正数，bn=n（1+）nan（n∈N+），e为自然对数的底数．‎ ‎（1）求函数f（x）=1+x﹣ex的单调区间，并比较（1+）n与e的大小；‎ ‎（2）计算，，，由此推测计算的公式，并给出证明；‎ ‎（3）令cn=（a1a2…an），数列{an}，{cn}的前n项和分别记为Sn，Tn，证明：Tn＜eSn．‎ ‎　‎ ‎2015年湖北省高考数学试卷（理科）‎ 参考答案与试题解析 ‎　‎ 一、选择题：本大题共10小题，每小题5分，共50分.在每小题给出的四个选项中，只有一项是符合题目要求的.‎ ‎1．（5分）（2015•湖北）i为虚数单位，i607的共轭复数为（　　）‎ A．i B．﹣i C．1 D．﹣1‎ ‎【分析】直接利用复数的单位的幂运算求解即可．‎ ‎【解答】解：i607=i604+3=i3=﹣i，‎ 它的共轭复数为：i．‎ 故选：A．‎ ‎　‎ ‎2．（5分）（2015•湖北）我国古代数学名著《九章算术》有“米谷粒分”题：粮仓开仓收粮，有人送来米1534石，验得米内夹谷，抽样取米一把，数得254粒内夹谷28粒，则这批米内夹谷约为（　　）‎ A．134石 B．169石 C．338石 D．1365石 ‎【分析】根据254粒内夹谷28粒，可得比例，即可得出结论．‎ ‎【解答】解：由题意，这批米内夹谷约为1534×≈169石，‎ 故选：B．‎ ‎　‎ ‎3．（5分）（2015•湖北）已知（1+x）n的展开式中第4项与第8项的二项式系数相等，则奇数项的二项式系数和为（　　）‎ A．212 B．211 C．210 D．29‎ ‎【分析】直接利用二项式定理求出n，然后利用二项式定理系数的性质求出结果即可．‎ ‎【解答】解：已知（1+x）n的展开式中第4项与第8项的二项式系数相等，‎ 可得，可得n=3+7=10．‎ ‎（1+x）10的展开式中奇数项的二项式系数和为：=29．‎ 故选：D．‎ ‎　‎ ‎4．（5分）（2015•湖北）设X～N（μ1，σ12），Y～N（μ2，σ22），这两个正态分布密度曲线如图所示．下列结论中正确的是（　　）‎ A．P（Y≥μ2）≥P（Y≥μ1） B．P（X≤σ2）≤P（X≤σ1）‎ C．对任意正数t，P（X≤t）≥P（Y≤t） D．对任意正数t，P（X≥t）≥P（Y≥t）‎ ‎【分析】直接利用正态分布曲线的特征，集合概率，直接判断即可．‎ ‎【解答】解：正态分布密度曲线图象关于x=μ对称，所以μ1＜μ2，从图中容易得到P（X≤t）≥P（Y≤t）．‎ 故选：C．‎ ‎　‎ ‎5．（5分）（2015•湖北）设a1，a2，…，an∈R，n≥3．若p：a1，a2，…，an成等比数列；q：（a12+a22+…+an﹣12）（a22+a32+…+an2）=（a1a2+a2a3+…+an﹣1an）2，则（　　）‎ A．p是q的充分条件，但不是q的必要条件 B．p是q的必要条件，但不是q的充分条件 C．p是q的充分必要条件 D．p既不是q的充分条件，也不是q的必要条件 ‎【分析】运用柯西不等式，可得：（a12+a22+…+an﹣12）（a22+a32+…+an2）≥（a1a2+a2a3+…+an﹣1an）2，讨论等号成立的条件，结合等比数列的定义和充分必要条件的定义，即可得到．‎ ‎【解答】解：由a1，a2，…，an∈R，n≥3．‎ 运用柯西不等式，可得：‎ ‎（a12+a22+…+an﹣12）（a22+a32+…+an2）≥（a1a2+a2a3+…+an﹣1an）2，‎ 若a1，a2，…，an成等比数列，即有==…=，‎ 则（a12+a22+…+an﹣12）（a22+a32+…+an2）=（a1a2+a2a3+…+an﹣1an）2，‎ 即由p推得q，‎ 但由q推不到p，比如a1=a2=a3=…=an=0，则a1，a2，…，an不成等比数列．‎ 故p是q的充分不必要条件．‎ 故选：A．‎ ‎　‎ ‎6．（5分）（2015•湖北）已知符号函数sgnx=，f（x）是R上的增函数，g（x）=f（x）﹣f（ax）（a＞1），则（　　）‎ A．sgn[g（x）]=sgnx B．sgn[g（x）]=﹣sgnx C．sgn[g（x）]=sgn[f（x）] D．sgn[g（x）]=﹣sgn[f（x）]‎ ‎【分析】直接利用特殊法，设出函数f（x），以及a的值，判断选项即可．‎ ‎【解答】解：由于本题是选择题，可以采用特殊法，符号函数sgnx=，f（x）是R上的增函数，g（x）=f（x）﹣f（ax）（a＞1），‎ 不妨令f（x）=x，a=2，‎ 则g（x）=f（x）﹣f（ax）=﹣x，‎ sgn[g（x）]=﹣sgnx．所以A不正确，B正确，‎ sgn[f（x）]=sgnx，C不正确；D正确；‎ 对于D，令f（x）=x+1，a=2，‎ 则g（x）=f（x）﹣f（ax）=﹣x，‎ sgn[f（x）]=sgn（x+1）=；‎ sgn[g（x）]=sgn（﹣x）=，‎ ‎﹣sgn[f（x）]=﹣sgn（x+1）=；所以D不正确；‎ 故选：B．‎ ‎　‎ ‎7．（5分）（2015•湖北）在区间[0，1]上随机取两个数x，y，记P1为事件“x+y≥”的概率，P2为事件“|x﹣y|≤”的概率，P3为事件“xy≤”的概率，则（　　）‎ A．P1＜P2＜P3 B．P2＜P3＜P1 C．P3＜P1＜P2 D．P3＜P2＜P1‎ ‎【分析】作出每个事件对应的平面区域，求出对应的面积，利用几何概型的概率公式进行计算比较即可．‎ ‎【解答】解：分别作出事件对应的图象如图（阴影部分）：‎ P1：D（0，），F（，0），A（0，1），B（1，1），C（1，0），‎ 则阴影部分的面积S1=1×1﹣=1﹣=，‎ S2=1×1﹣2×=1﹣=，‎ S3=1×+dx=+lnx|=﹣ln=+ln2，‎ ‎∴S2＜S3＜S1，‎ 即P2＜P3＜P1，‎ 故选：B．‎ ‎　‎ ‎8．（5分）（2015•湖北）将离心率为e1的双曲线C1的实半轴长a和虚半轴长b（a≠b）同时增加m（m＞0）个单位长度，得到离心率为e2的双曲线C2，则（　　）‎ A．对任意的a，b，e1＞e2‎ B．当a＞b时，e1＞e2；当a＜b时，e1＜e2‎ C．对任意的a，b，e1＜e2‎ D．当a＞b时，e1＜e2；当a＜b时，e1＞e2‎ ‎【分析】分别求出双曲线的离心率，再平方作差，即可得出结论．‎ ‎【解答】解：由题意，双曲线C1：c2=a2+b2，e1=；‎ 双曲线C2：c′2=（a+m）2+（b+m）2，e2=，‎ ‎∴=﹣=，‎ ‎∴当a＞b时，e1＜e2；当a＜b时，e1＞e2，‎ 故选：D．‎ ‎　‎ ‎9．（5分）（2015•湖北）已知集合A={（x，y）|x2+y2≤1，x，y∈Z}，B={（x，y）||x|≤2，|y|≤2，x，y∈Z}，定义集合A⊕B={（x1+x2，y1+y2）|（x1，y1）∈A，（x2，y2）∈B}，则A⊕B中元素的个数为（　　）‎ A．77 B．49 C．45 D．30‎ ‎【分析】由题意可得，A={（0，0），（0，1），（0，﹣1），（1，0），（﹣1，0），B={（0，0），（0，1），（0，2），（0，﹣1），（0，﹣2），（1，0），（1，1），（1，2）（1，﹣1），（1，﹣2）（2，0），（2，1），（2，2）（2，﹣1），（2，﹣2），（﹣1，﹣2），（﹣1，﹣1），（﹣1，0），（﹣1，1），（﹣1，2），（﹣2，﹣2），（﹣2，﹣1），（﹣2，0），（﹣2，1），（﹣2，2）}，根据定义可求 ‎【解答】解：解法一：‎ ‎∵A={（x，y）|x2+y2≤1，x，y∈Z}={（0，0），（0，1），（0，﹣1），（1，0），（﹣1，0），‎ B={（x，y）||x|≤2，|y|≤2，x，y∈Z}={（0，0），（0，1），（0，2），（0，﹣1），（0，﹣2），（1，0），（1，1），（1，2）（1，﹣1），（1，﹣2）（2，0），（2，1），（2，2）（2，﹣1），（2，﹣2），（﹣1，﹣2），（﹣1，﹣1），（﹣1，0），（﹣1，1），（﹣1，2），（﹣2，﹣2），（﹣2，﹣1），（﹣2，0），（﹣2，1），（﹣2，2）}‎ ‎∵A⊕B={（x1+x2，y1+y2）|（x1，y1）∈A，（x2，y2）∈B}，‎ ‎∴A⊕B={‎ ‎（0，0），（0，1），（0，2），（0，﹣1），（0，﹣2），（1，0），（1，1），（1，2）（1，﹣1），（1，﹣2）（2，0），（2，1），（2，2），（2，﹣1），（2，﹣2），（﹣1，﹣2），（﹣1，﹣1），（﹣1，0），（﹣1，1），（﹣1，2），（﹣2，﹣2），（﹣2，﹣1），（﹣2，0），（﹣2，1），（﹣2，2），‎ ‎（﹣2，3），（﹣2，﹣3），（0，﹣3），（2，﹣3），（﹣1，3），（﹣1，﹣3），（1，3），（2，3），（0，3），（3，﹣1），（3，0）（3，1），（3，2），（3，﹣2）（﹣3，2）（﹣3，1），（1，﹣3），（﹣3，﹣1），（﹣3，0），（﹣3，﹣2）}共45个元素；‎ 解法二：‎ 因为集合A={（x，y）|x2+y2≤1，x，y∈Z}，所以集合A中有5个元素，即图中圆中的整点，B={（x，y）||x|≤2，|y|≤2，x，y∈Z}，中有5×5=25个元素，即图中正方形ABCD中的整点，A⊕B={（x1+x2，y1+y2）|（x1，y1）∈A，（x2，y2）∈B}的元素可看作正方形A1B1C1D1中的整点（除去四个顶点），即7×7﹣4=45个．‎ 故选：C．‎ ‎　‎ ‎10．（5分）（2015•湖北）设x∈R，[x]表示不超过x的最大整数．若存在实数t，使得[t]=1，[t2]=2，…，[tn]=n同时成立，则正整数n的最大值是（　　）‎ A．3 B．4 C．5 D．6‎ ‎【分析】由新定义可得t的范围，验证可得最大的正整数n为4．‎ ‎【解答】解：若[t]=1，则t∈[1，2），‎ 若[t2]=2，则t∈[，）（因为题目需要同时成立，则负区间舍去），‎ 若[t3]=3，则t∈[，），‎ 若[t4]=4，则t∈[，），‎ 若[t5]=5，则t∈[，），‎ 其中≈1.732，≈1.587，≈1.495，≈1.431＜1.495，‎ 通过上述可以发现，当t=4时，可以找到实数t使其在区间[1，2）∩[，）∩[，）∩[，）上，‎ 但当t=5时，无法找到实数t使其在区间[1，2）∩[，）∩[，）∩[，）∩[，）‎ 上，‎ ‎∴正整数n的最大值4‎ 故选：B．‎ ‎　‎ 二、填空题：本大题共4小题，考生需作答5小题，每小题5分，共25分．请将答案填在答题卡对应题号的位置上．答错位置，书写不清，模棱两可均不得分．‎ ‎11．（5分）（2015•湖北）已知向量⊥，||=3，则•=　9　．‎ ‎【分析】由已知结合平面向量是数量积运算求得答案．‎ ‎【解答】解：由⊥，得•=0，即•（）=0，‎ ‎∵||=3，‎ ‎∴．‎ 故答案为：9．‎ ‎　‎ ‎12．（5分）（2015•湖北）函数f（x）=4cos2cos（﹣x）﹣2sinx﹣|ln（x+1）|的零点个数为　2　．‎ ‎【分析】利用二倍角公式化简函数的解析式，求出函数的定义域，画出函数的图象，求出交点个数即可．‎ ‎【解答】解：函数f（x）的定义域为：{x|x＞﹣1}．‎ f（x）=4cos2cos（﹣x）﹣2sinx﹣|ln（x+1）|‎ ‎=2sinx﹣|ln（x+1）|‎ ‎=sin2x﹣|ln（x+1）|，‎ 分别画出函数y=sin2x，y=|ln（x+1）|的图象，‎ 由函数的图象可知，交点个数为2．‎ 所以函数的零点有2个．‎ 故答案为：2．‎ ‎　‎ ‎13．（5分）（2015•湖北）如图，一辆汽车在一条水平的公路上向正西行驶，到A处时测得公路北侧一山顶D在西偏北30°的方向上，行驶600m后到达B处，测得此山顶在西偏北75°的方向上，仰角为30°，则此山的高度CD=　100　m．‎ ‎【分析】设此山高h（m），在△BCD中，利用仰角的正切表示出BC，进而在△ABC中利用正弦定理求得h．‎ ‎【解答】解：设此山高h（m），则BC=h，‎ 在△ABC中，∠BAC=30°，∠CBA=105°，∠BCA=45°，AB=600．‎ 根据正弦定理得=，‎ 解得h=100（m）‎ 故答案为：100．‎ ‎　‎ ‎14．（5分）（2015•湖北）如图，圆C与x轴相切于点T（1，0），与y轴正半轴交于两点A，B（B在A的上方），且|AB|=2．‎ ‎（1）圆C的标准方程为　（x﹣1）2+（y﹣）2=2　；‎ ‎（2）过点A任作一条直线与圆O：x2+y2=1相交于M，N两点，下列三个结论：‎ ‎①=； ②﹣=2； ③+=2．‎ 其中正确结论的序号是　①②③　．（写出所有正确结论的序号）‎ ‎【分析】（1）取AB的中点E，通过圆C与x轴相切于点T，利用弦心距、半径与半弦长之间的关系，计算即可；‎ ‎（2）设M（cosα，sinα），N（cosβ，sinβ），计算出、、的值即可．‎ ‎【解答】解：（1）∵圆C与x轴相切于点T（1，0），‎ ‎∴圆心的横坐标x=1，取AB的中点E，‎ ‎∵|AB|=2，∴|BE|=1，‎ 则|BC|=，即圆的半径r=|BC|=，‎ ‎∴圆心C（1，），‎ 则圆的标准方程为（x﹣1）2+（y﹣）2=2，‎ 故答案为：（x﹣1）2+（y﹣）2=2．‎ ‎（2）∵圆心C（1，），∴E（0，），‎ 又∵|AB|=2，且E为AB中点，‎ ‎∴A（0，﹣1），B（0，+1），‎ ‎∵M、N在圆O：x2+y2=1上，‎ ‎∴可设M（cosα，sinα），N（cosβ，sinβ），‎ ‎∴|NA|=‎ ‎=‎ ‎=‎ ‎=‎ ‎=，‎ ‎|NB|=‎ ‎=‎ ‎=‎ ‎=，‎ ‎∴===，‎ 同理可得=，‎ ‎∴=，①成立，‎ ‎﹣=﹣（）=2，②正确．‎ ‎+=+（）=，③正确．‎ 故答案为：①②③．‎ ‎　‎ 选修4-1：几何证明选讲 ‎15．（5分）（2015•湖北）如图，PA是圆的切线，A为切点，PBC是圆的割线，且BC=3PB，则=　　．‎ ‎【分析】利用切割线定理推出PA=2PB，利用相似三角形求出比值即可．‎ ‎【解答】解：由切割线定理可知：PA2=PB•PC，又BC=3PB，‎ 可得PA=2PB，‎ 在△PAB与△PAC中，∠P=∠P，∠PAB=∠PCA（同弧上的圆周角与弦切角相等），‎ 可得△PAB∽△PAC，‎ ‎∴==．‎ 故答案为：．‎ ‎　‎ 选修4-4：坐标系与参数方程 ‎16．（2015•湖北）在直角坐标系xOy中，以O为极点，x轴的正半轴为极轴建立极坐标系．已知直线l的极坐标方程为ρ（sinθ﹣3cosθ）=0，曲线C的参数方程为（ t为参数），l与C相交于A，B两点，则|AB|=　　．‎ ‎【分析】化极坐标方程化直角坐标方程，参数方程化普通方程，联立直线方程和双曲线方程后求得交点坐标，由两点间的距离公式得答案．‎ ‎【解答】解：由ρ（sinθ﹣3cosθ）=0，得y﹣3x=0，‎ 由C的参数方程为（ t为参数），两式平方作差得：x2﹣y2=﹣4．‎ 联立，得，即．‎ ‎∴A（），B（），‎ ‎∴|AB|=．‎ 故答案为：．‎ ‎　‎ 三、解答题：本大题共6小题，共75分．解答应写出文字说明、证明过程或演算步骤．‎ ‎17．（11分）（2015•湖北）某同学用“五点法”画函数f（x）=Asin（ωx+φ）（ω＞0，|φ|＜）在某一个周期内的图象时，列表并填入了部分数据，如表：‎ ωx+φ ‎0‎ π ‎2π x Asin（ωx+φ）‎ ‎0‎ ‎5‎ ‎﹣5‎ ‎0‎ ‎（1）请将上表数据补充完整，填写在相应位置，并直接写出函数f（x）的解析式；‎ ‎（2）将y=f（x）图象上所有点向左平行移动θ（θ＞0）个单位长度，得到y=g（x）的图象．若y=g（x）图象的一个对称中心为（，0），求θ的最小值．‎ ‎【分析】（1）根据表中已知数据，解得A=5，ω=2，φ=﹣．从而可补全数据，解得函数表达式为f（x）=5sin（2x﹣）．‎ ‎（2）由（Ⅰ）及函数y=Asin（ωx+φ）的图象变换规律得g（x）=5sin（2x+2θ﹣）．令2x+2θ﹣=kπ，解得x=，k∈Z．令=，解得θ=，k∈Z．由θ＞0可得解．‎ ‎【解答】解：（1）根据表中已知数据，解得A=5，ω=2，φ=﹣．数据补全如下表：‎ ωx+φ ‎0‎ π ‎2π x Asin（ωx+φ）‎ ‎0‎ ‎5‎ ‎0‎ ‎﹣5‎ ‎0‎ 且函数表达式为f（x）=5sin（2x﹣）．‎ ‎（2）由（Ⅰ）知f（x）=5sin（2x﹣），得g（x）=5sin（2x+2θ﹣）．‎ 因为y=sinx的对称中心为（kπ，0），k∈Z．‎ 令2x+2θ﹣=kπ，解得x=，k∈Z．‎ 由于函数y=g（x）的图象关于点（，0）成中心对称，令=，‎ 解得θ=，k∈Z．由θ＞0可知，当K=1时，θ取得最小值．‎ ‎　‎ ‎18．（12分）（2015•湖北）设等差数列{an}的公差为d，前n项和为Sn，等比数列{bn}的公比为q，已知b1=a1，b2=2，q=d，S10=100．‎ ‎（1）求数列{an}，{bn}的通项公式 ‎（2）当d＞1时，记cn=，求数列{cn}的前n项和Tn．‎ ‎【分析】（1）利用前10项和与首项、公差的关系，联立方程组计算即可；‎ ‎（2）当d＞1时，由（1）知cn=，写出Tn、Tn的表达式，利用错位相减法及等比数列的求和公式，计算即可．‎ ‎【解答】解：（1）设a1=a，由题意可得，‎ 解得，或，‎ 当时，an=2n﹣1，bn=2n﹣1；‎ 当时，an=（2n+79），bn=9•；‎ ‎（2）当d＞1时，由（1）知an=2n﹣1，bn=2n﹣1，‎ ‎∴cn==，‎ ‎∴Tn=1+3•+5•+7•+9•+…+（2n﹣1）•，‎ ‎∴Tn=1•+3•+5•+7•+…+（2n﹣3）•+（2n﹣1）•，‎ ‎∴Tn=2+++++…+﹣（2n﹣1）•=3﹣，‎ ‎∴Tn=6﹣．‎ ‎　‎ ‎19．（12分）（2015•湖北）《九章算术》中，将底面为长方形且有一条侧棱与底面垂直的四棱锥称之为阳马，将四个面都为直角三角形的四面体称之为鳖臑．如图，在阳马P﹣ABCD中，侧棱PD⊥底面ABCD，且PD=CD，过棱PC的中点E，作EF⊥PB交PB于点F，连接DE，DF，BD，BE．‎ ‎（1）证明：PB⊥平面DEF．试判断四面体DBEF是否为鳖臑，若是，写出其每个面的直角（只需写出结论）；若不是，说明理由；‎ ‎（2）若面DEF与面ABCD所成二面角的大小为，求的值．‎ ‎【分析】解法1）（1）直线与直线，直线与平面的垂直的转化证明得出PB⊥EF，DE∩FE=E，所以PB⊥平面DEF，即可判断DE⊥平面PBC，PB⊥平面DEF，可知四面体BDEF的四个面都是直角三角形，确定直角．‎ ‎（2）根据公理2得出DG是平面DEF与平面ACBD的交线．利用直线平面的垂直判断出DG⊥DF，DG⊥DB，根据平面角的定义得出∠BDF是面DEF与面ABCD所成二面角的平面角，转化到直角三角形求解即可．‎ 解法2）‎ ‎（1）以D为原点，射线DA，DC，DP分别为x，y，z轴的正半轴，建立空间直角坐标系，运用向量的数量积判断即可．‎ ‎2）由PD⊥底面ABCD，所以=（0，0，1）是平面ACDB的一个法向量；由（Ⅰ）知，PB⊥平面DEF，所以=（﹣λ，﹣1，1）是平面DEF的一个法向量．根据数量积得出夹角的余弦即可得出所求解的答案．‎ ‎【解答】解法1）（1）因为PD⊥底面ABCD，所以PD⊥BC，‎ 由底面ABCD为长方形，有BC⊥CD，而PD∩CD=D，‎ 所以BC⊥平面PCD．而DE⊂平面PDC，所以BC⊥DE．‎ 又因为PD=CD，点E是PC的中点，所以DE⊥PC．‎ 而PC∩CB=C，所以DE⊥平面PBC．而PB⊂平面PBC，所以PB⊥DE．‎ 又PB⊥EF，DE∩FE=E，所以PB⊥平面DEF．‎ 由DE⊥平面PBC，PB⊥平面DEF，可知四面体BDEF的四个面都是直角三角形，‎ 即四面体BDEF是一个鳖臑，其四个面的直角分别为∠DEB，∠DEF，∠EFB，∠DFB．‎ ‎（2）如图1，‎ 在面BPC内，延长BC与FE交于点G，则DG是平面DEF与平面ACBD的交线．‎ 由（Ⅰ）知，PB⊥平面DEF，所以PB⊥DG．‎ 又因为PD⊥底面ABCD，所以PD⊥DG．而PD∩PB=P，所以DG⊥平面PBD．‎ 所以DG⊥DF，DG⊥DB 故∠BDF是面DEF与面ABCD所成二面角的平面角，‎ 设PD=DC=1，BC=λ，有BD=，‎ 在Rt△PDB中，由DF⊥PB，得∠DGF=∠FDB=，‎ 则 tan=tan∠DPF===，解得．‎ 所以==‎ 故当面DEF与面ABCD所成二面角的大小为时，=．‎ ‎（解法2）‎ ‎（1）以D为原点，射线DA，DC，DP分别为x，y，z轴的正半轴，建立空间直角坐标系．设PD=DC=1，BC=λ，‎ 则D（0，0，0），P（0，0，1），B（λ，1，0），C（0，1，0），=（λ1，﹣1），点E是PC的中点，所以E（0，，），=（0，，），‎ 于是=0，即PB⊥DE．‎ 又已知EF⊥PB，而ED∩EF=E，所以PB⊥平面DEF．‎ 因=（0，1，﹣1），=0，则DE⊥PC，所以DE⊥平面PBC．‎ 由DE⊥平面PBC，PB⊥平面DEF，可知四面体BDEF的四个面都是直角三角形，‎ 即四面体BDEF是一个鳖臑，其四个面的直角分别为∠DEB，∠DEF，∠EFB，∠‎ DFB．‎ ‎（2）由PD⊥底面ABCD，所以=（0，0，1）是平面ACDB的一个法向量；‎ 由（Ⅰ）知，PB⊥平面DEF，所以=（﹣λ，﹣1，1）是平面DEF的一个法向量．‎ 若面DEF与面ABCD所成二面角的大小为，‎ 则运用向量的数量积求解得出cos==，‎ 解得．所以所以==‎ 故当面DEF与面ABCD所成二面角的大小为时，=．‎ ‎　‎ ‎20．（12分）（2015•湖北）某厂用鲜牛奶在某台设备上生产A，B两种奶制品．生产1吨A产品需鲜牛奶2吨，使用设备1小时，获利1000元；生产1吨B产品需鲜牛奶1.5吨，使用设备1.5小时，获利1200元．要求每天B产品的产量不超过A产品产量的2倍，设备每天生产A，B两种产品时间之和不超过12小时．假定每天可获取的鲜牛奶数量W（单位：吨）是一个随机变量，其分布列为 W ‎12‎ ‎15‎ ‎18‎ P ‎0.3‎ ‎0.5‎ ‎0.2‎ 该厂每天根据获取的鲜牛奶数量安排生产，使其获利最大，因此每天的最大获利Z（单位：元）是一个随机变量．‎ ‎（1）求Z的分布列和均值；‎ ‎（2）若每天可获取的鲜牛奶数量相互独立，求3天中至少有1天的最大获利超过10000元的概率．‎ ‎【分析】（1）设每天A，B两种产品的生产数量分别为x，y，相应的获利为z，列出可行域，目标函数，通过当W=12时，当W=15时，当W=18时，分别求出目标函数的最大获利，然后得到Z的分布列．求出期望即可．‎ ‎（2）判断概率类型是二项分布，然后求解所求概率即可．‎ ‎【解答】（12分）‎ 解：（1）设每天A，B两种产品的生产数量分别为x，y，相应的获利为z，则有 ‎，①如图1，目标函数为：z=1000x+1200y．‎ 当W=12时，①表示的平面区域如图1，三个顶点分别为A（0，0），B（2.4，4.8），C（6，0）．‎ 将z=1000x+1200y变形为，‎ 当x=2.4，y=4.8时，直线l：在y轴上的截距最大，‎ 最大获利Z=Zmax=2.4×1000+4.8×1200=8160．‎ 当W=15时，①表示的平面区域如图2，三个顶点分别为A（0，0），B（3，6），C（7.5，0）．．‎ 将z=1000x+1200y变形为，‎ 当x=3，y=6时，直线l：在y轴上的截距最大，‎ 最大获利Z=Zmax=3×1000+6×1200=10200．‎ 当W=18时，①表示的平面区域如图3，四个顶点分别为A（0，0），B（3，6），C（6，4），D（9，0）．‎ 将z=1000x+1200y变形为：，‎ 当x=6，y=4时，直线l：y=﹣56x+z1200在y轴上的截距最大，最大获利Z=Zmax=6×1000+4×1200=10800．‎ 故最大获利Z的分布列为：‎ Z ‎8160‎ ‎10200‎ ‎10800‎ P ‎0.3‎ ‎0.5‎ ‎0.2‎ 因此，E（Z）=8160×0.3+10200×0.5+10800×0.2=9708‎ ‎（2）由（Ⅰ）知，一天最大获利超过10000元的概率P1=P（Z＞10000）=0.5+0.2=0.7，‎ 由二项分布，3天中至少有1天最大获利超过10000元的概率为：‎ ‎．‎ ‎　‎ ‎21．（14分）（2015•湖北）一种画椭圆的工具如图1所示．O是滑槽AB的中点，短杆ON可绕O转动，长杆MN通过N处铰链与ON连接，MN上的栓子D可沿滑槽AB滑动，且DN=ON=1，MN=3，当栓子D在滑槽AB内作往复运动时，带动N绕O转动，M处的笔尖画出的椭圆记为C，以O为原点，AB所在的直线为x轴建立如图2所示的平面直角坐标系．‎ ‎（1）求椭圆C的方程；‎ ‎（2）设动直线l与两定直线l1：x﹣2y=0和l2：x+2y=0分别交于P，Q两点．若直线l总与椭圆C有且只有一个公共点，试探究：△OPQ的面积是否存在最小值？若存在，求出该最小值；若不存在，说明理由．‎ ‎【分析】（1）根据条件求出a，b即可求椭圆C的方程；‎ ‎（2）联立直线方程和椭圆方程，求出原点到直线的距离，结合三角形的面积公式进行求解即可．‎ ‎【解答】解：（1）设D（t，0），|t|≤2，‎ N（x0，y0），M（x，y），由题意得=2，‎ 且||=||=1，‎ ‎∴（t﹣x，﹣y）=2（x0﹣t，y0），且，‎ 即，且t（t﹣2x0）=0，‎ 由于当点D不动时，点N也不动，∴t不恒等于0，‎ 于是t=2x0，故x0=，y0=﹣，‎ 代入x02+y02=1，得方程为．‎ ‎（2）①当直线l的斜率k不存在时，直线l为：x=4或x=﹣4，都有S△OPQ=，‎ ‎②直线l的斜率k存在时，直线l为：y=kx+m，（k），‎ 由消去y，可得（1+4k2）x2+8kmx+4m2﹣16=0，‎ ‎∵直线l总与椭圆C有且只有一个公共点，‎ ‎∴△=64k2m2﹣4（1+4k2）（4m2﹣16）=0，即m2=16k2+4，①，‎ 由，可得P（，），同理得Q（，），‎ 原点O到直线PQ的距离d=和|PQ|=•|xP﹣xQ|，‎ 可得S△OPQ=|PQ|d=|m||xP﹣xQ|=|m|||=||②，‎ 将①代入②得S△OPQ=||=8||，‎ 当k2＞时，S△OPQ=8（）=8（1+）＞8，‎ 当0≤k2＜时，S△OPQ=8||=﹣8（）=8（﹣1+），‎ ‎∵0≤k2＜时，∴0＜1﹣4k2≤1，≥2，‎ ‎∴S△OPQ=8（﹣1+）≥8，当且仅当k=0时取等号，‎ ‎∴当k=0时，S△OPQ的最小值为8，‎ 综上可知当直线l与椭圆C在四个顶点处相切时，三角形OPQ的面积存在最小值为8．‎ ‎　‎ ‎22．（14分）（2015•湖北）已知数列{an}的各项均为正数，bn=n（1+）nan（n∈N+），e为自然对数的底数．‎ ‎（1）求函数f（x）=1+x﹣ex的单调区间，并比较（1+）n与e的大小；‎ ‎（2）计算，，，由此推测计算的公式，并给出证明；‎ ‎（3）令cn=（a1a2…an），数列{an}，{cn}的前n项和分别记为Sn，Tn，证明：Tn＜eSn．‎ ‎【分析】（1）求出f（x）的定义域，利用导数求其最大值，得到1+x＜ex．取x=即可得到答案；‎ ‎（2）由bn=n（1+）nan（n∈N+），变形求得，，，由此推测=（n+1）n．然后利用数学归纳法证明．‎ ‎（3）由cn的定义、=（n+1）n、算术﹣几何平均不等式、bn的定义及，利用放缩法证得Tn＜eSn．‎ ‎【解答】（1）解：f（x）的定义域为（﹣∞，+∞），f′（x）=1﹣ex．‎ 当f′（x）＞0，即x＜0时，f（x）单调递增；‎ 当f′（x）＜0，即x＞0时，f（x）单调递减．‎ 故f（x）的单调递增区间为（﹣∞，0），单调递减区间为（0，+∞）．‎ 当x＞0时，f（x）＜f（0）=0，即1+x＜ex．‎ 令，得，即．①‎ ‎（2）解：；=；‎ ‎．‎ 由此推测：=（n+1）n．②‎ 下面用数学归纳法证明②．‎ ‎（1）当n=1时，左边=右边=2，②成立．‎ ‎（2）假设当n=k时，②成立，即．‎ 当n=k+1时，，由归纳假设可得 ‎=．‎ ‎∴当n=k+1时，②也成立．‎ 根据（1）（2），可知②对一切正整数n都成立．‎ ‎（3）证明：由cn的定义，②，算术﹣几何平均不等式，bn的定义及①得 Tn=c1+c2+…+cn=‎ ‎=‎ ‎=‎ ‎=‎ ‎=‎ ‎＜ea1+ea2+…+ean=eSn．‎ 即Tn＜eSn．‎ ‎　‎ 参与本试卷答题和审题的老师有：qiss；刘长柏；双曲线；maths；吕静；lincy；sxs123；cst；w3239003；sdpyqzh（排名不分先后）‎ ‎2017年2月3日