高中数学（人教版a版必修一）配套课时作业：第一章集合与函数的概念1-2-2第1课时word版含解析 6页

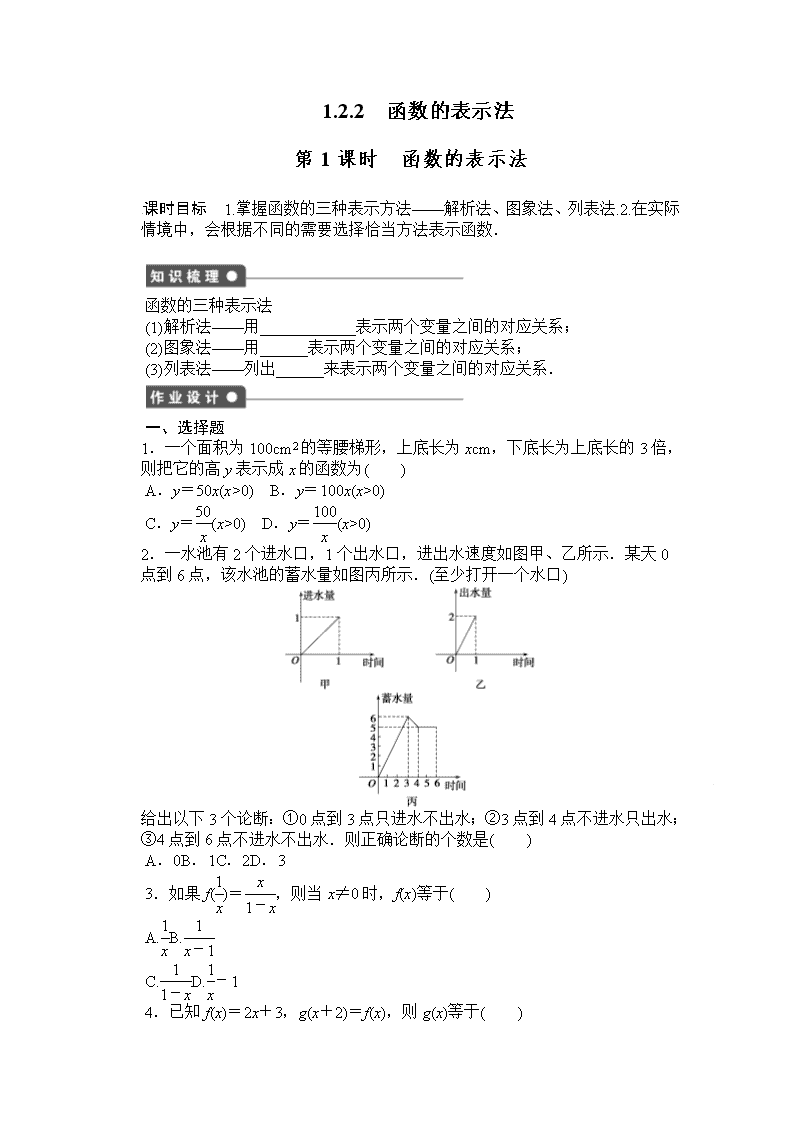
1.2.2 函数的表示法 第 1 课时 函数的表示法 课时目标 1.掌握函数的三种表示方法——解析法、图象法、列表法.2.在实际 情境中，会根据不同的需要选择恰当方法表示函数． 函数的三种表示法 (1)解析法——用____________表示两个变量之间的对应关系； (2)图象法——用______表示两个变量之间的对应关系； (3)列表法——列出______来表示两个变量之间的对应关系． 一、选择题 1．一个面积为 100cm2 的等腰梯形，上底长为 xcm，下底长为上底长的 3 倍， 则把它的高 y 表示成 x 的函数为( ) A．y＝50x(x>0) B．y＝100x(x>0) C．y＝50 x (x>0) D．y＝100 x (x>0) 2．一水池有 2 个进水口，1 个出水口，进出水速度如图甲、乙所示．某天 0 点到 6 点，该水池的蓄水量如图丙所示．(至少打开一个水口) 给出以下 3 个论断：①0 点到 3 点只进水不出水；②3 点到 4 点不进水只出水； ③4 点到 6 点不进水不出水．则正确论断的个数是( ) A．0B．1C．2D．3 3．如果 f(1 x)＝ x 1－x ，则当 x≠0 时，f(x)等于( ) A.1 xB. 1 x－1 C. 1 1－xD.1 x －1 4．已知 f(x)＝2x＋3，g(x＋2)＝f(x)，则 g(x)等于( ) A．2x＋1B．2x－1 C．2x－3D．2x＋7 5．若 g(x)＝1－2x，f[g(x)]＝1－x2 x2 ，则 f(1 2)的值为( ) A．1B．15C．4D．30 6．在函数 y＝|x|(x∈[－1,1])的图象上有一点 P(t，|t|)，此函数与 x 轴、直线 x ＝－1 及 x＝t 围成图形(如图阴影部分)的面积为 S，则 S 与 t 的函数关系图可表 示为( ) 题 号 1 2 3 4 5 6 答 案 二、填空题 7．一个弹簧不挂物体时长 12cm，挂上物体后会伸长，伸长的长度与所挂物体 的质量成正比例．如果挂上 3kg 物体后弹簧总长是 13.5cm，则弹簧总长 y(cm) 与所挂物体质量 x(kg)之间的函数关系式为 ___________________________________________________________________ _____． 8．已知函数 y＝f(x)满足 f(x)＝2f(1 x)＋x，则 f(x)的解析式为____________． 9．已知 f(x)是一次函数，若 f(f(x))＝4x＋8，则 f(x)的解析式为 __________________． 三、解答题 10．已知二次函数 f(x)满足 f(0)＝f(4)，且 f(x)＝0 的两根平方和为 10，图象过(0,3) 点，求 f(x)的解析式． 11．画出函数 f(x)＝－x2＋2x＋3 的图象，并根据图象回答下列问题： (1)比较 f(0)、f(1)、f(3)的大小； (2)若 x10)．] 2．B [由题意可知在 0 点到 3 点这段时间，每小时进水量为 2，即 2 个进水 口同时进水且不出水，所以①正确；从丙图可知 3 点到 4 点水量减少了 1，所 以应该是有一个进水口进水，同时出水口也出水，故②错；当两个进水口同时 进水，出水口也同时出水时，水量保持不变，也可由题干中的“至少打开一个 水口”知③错．] 3．B [令1 x ＝t，则 x＝1 t ，代入 f(1 x)＝ x 1－x ， 则有 f(t)＝ 1 t 1－1 t ＝ 1 t－1 ，故选 B.] 4．B [由已知得：g(x＋2)＝2x＋3，令 t＝x＋2，则 x＝t－2，代入 g(x＋2)＝ 2x＋3，则有 g(t)＝2(t－2)＋3＝2t－1，故选 B.] 5．B [令 1－2x＝1 2 ，则 x＝1 4 ， ∴f(1 2)＝ 1－1 4 2 1 4 2 ＝15.] 6．B [当 t<0 时，S＝1 2 －t2 2 ，所以图象是开口向下的抛物线，顶点坐标是(0， 1 2)；当 t>0 时，S＝1 2 ＋t2 2 ，开口是向上的抛物线，顶点坐标是(0，1 2)．所以 B 满 足要求．] 7．y＝1 2x＋12 解析 设所求函数解析式为 y＝kx＋12，把 x＝3，y＝13.5 代入，得 13.5＝3k ＋12，k＝1 2. 所以所求的函数解析式为 y＝1 2x＋12. 8．f(x)＝－x2＋2 3x (x≠0) 解析 ∵f(x)＝2f(1 x)＋x，① ∴将 x 换成1 x ，得 f(1 x)＝2f(x)＋1 x.② 由①②消去 f(1 x)，得 f(x)＝－ 2 3x －x 3 ， 即 f(x)＝－x2＋2 3x (x≠0)． 9．f(x)＝2x＋8 3 或 f(x)＝－2x－8 解析 设 f(x)＝ax＋b(a≠0)， 则 f(f(x))＝f(ax＋b)＝a2x＋ab＋b. ∴ a2＝4 ab＋b＝8 ，解得 a＝2 b＝8 3 或 a＝－2 b＝－8 . 10．解 设 f(x)＝ax2＋bx＋c(a≠0)． 由 f(0)＝f(4)知 f0＝c， f4＝16a＋4b＋c， f0＝f4， 得 4a＋b＝0.① 又图象过(0,3)点， 所以 c＝3.② 设 f(x)＝0 的两实根为 x1，x2， 则 x1＋x2＝－b a ，x1·x2＝c a. 所以 x21＋x22＝(x1＋x2)2－2x1x2＝(－b a)2－2·c a ＝10. 即 b2－2ac＝10a2.③ 由①②③得 a＝1，b＝－4，c＝3.所以 f(x)＝x2－4x＋3. 11．解 因为函数 f(x)＝－x2＋2x＋3 的定义域为 R，列表： x … －2 －1 0 1 2 3 4 … y … －5 0 3 4 3 0 －5 … 连线，描点，得函数图象如图： (1)根据图象，容易发现 f(0)＝3，f(1)＝4，f(3)＝0， 所以 f(3)