人教A版高中数学必修一131单调性与最大小值1模板 28页

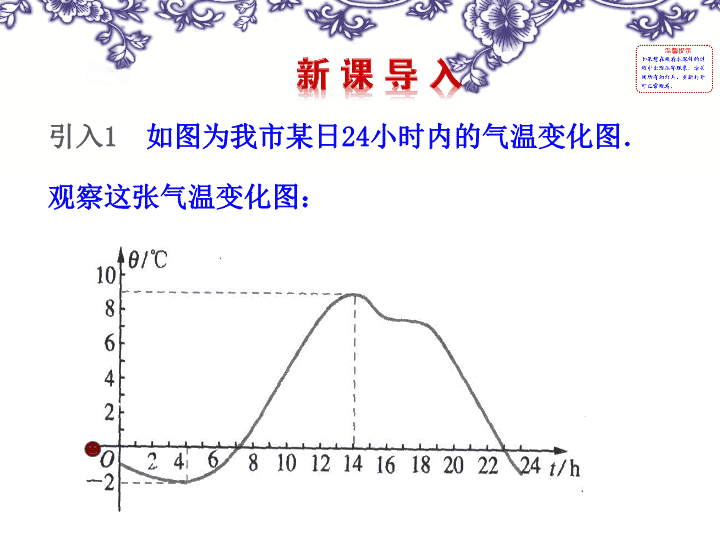
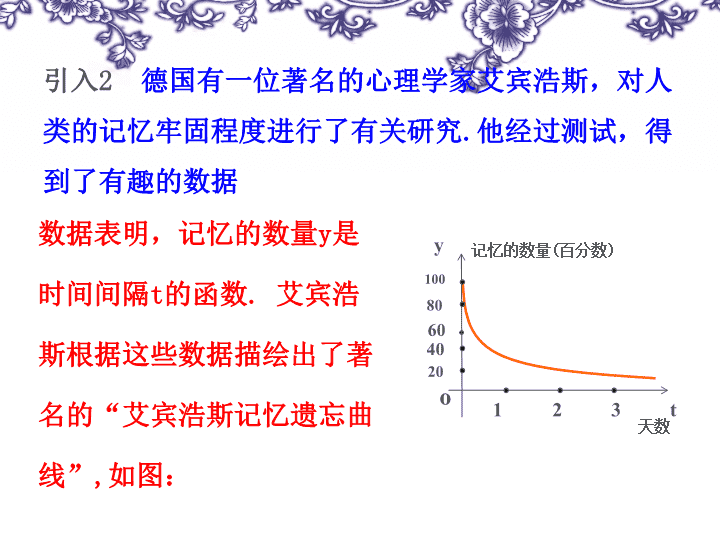
1.3 函数的基本性质 1.3.1 单调性与最大（小）值 第 1 课时 函数的单调性 引入 1 如图为我市某日 24 小时内的气温变化图．观察这张气温变化图： 引入 2 德国有一位著名的心理学家艾宾浩斯，对人类的记忆牢固程度进行了有关研究 . 他经过测试，得到了有趣的数据 数据表明，记忆的数量 y 是时间间隔 t 的函数 . 艾宾浩斯根据这些数据描绘出了著名的“艾宾浩斯记忆遗忘曲线” , 如图： 1 2 3 t y o 20 40 60 80 记忆的数量 ( 百分数 ) 天数 100 思考 1 ： 当时间间隔 t 逐渐增大时，你能看出对应的函数值 y 有什么变化趋势？通过这个实验， 你打算以后如何对待刚学过的 知识 ? 思考 2: “ 艾宾浩斯记忆遗忘曲线” 从左至右是逐渐下降的，对此， 我们如何用数学观点进行解释？ 1 2 3 t y o 20 40 60 80 100 记忆的数量 ( 百分数 ) 天数 1. 理解单调函数的定义； （重点） 2. 理解增函数、减函数的定义； （重点） 3. 掌握定义法判断函数单调性的步骤； （难点） 4. 会用函数单调性的定义证明简单的函数的单调性，求函数的单调区间 . 我们通过几个函数的图象观察函数值随自变量而变化的规律 . 探究点 函数单调性的定义 这种函数在其定义域的一个区间上函数值随 着自变量的 ___________ 的性质我们称之为 “函 数在这个区间上是增函数” ；函数在其定义域的 一个区间上函数值随着自变量的 ___________ 的 性质我们称之为 “函数在这个区间上是减函数” . 如何用函数的解析式和数学语言进行描绘？ 增大而增大 增大而减少 对函数 f(x)=x 2 而言，“函数值在（ 0 ， +∞ ）上随 自变量的增大而增大”，可以这样描述：在区间 （ 0 ， +∞ ）上任取两个实数 x 1 ,x 2 , 得到函数值 f(x 1 )=x 1 2 ,f(x 2 )=x 2 2 ，当 x 1 f(x 2 ) 增函数或减函数 第一、在中学数学中所说的单调性是指严格的单调性 , 即必须是 f(x 1 )f(x 2 )), 而不能是 f(x 1 )≤f(x 2 ) ( 或 f(x 1 )≥f(x 2 )); 对函数单调性的理解 第二、函数的单调性是对定义域内的某个区间而言的 , 是局部概念 ; 第三、学习函数的单调性 , 要注意定义中条件和结论是双向使用的 . 例 1. 下图是定义在区间 [-5,5] 上的函数 y=f(x) ，根据 图象说出函数的单调区间，以及在每一个单调区间上，它是增函数还是减函数 ? 解： 函数 的单调区间有 其中 在区间 上是减函数，在区间 上是增函数． 整个上午（ 8 ： 00—12 ： 00 ）天气越来越暖， 中午时分（ 12 ： 00—13 ： 00 ）一场暴风雨使天气骤 然凉爽了许多 . 暴风雨过后，天气转暖，直到太阳 下山（ 18 ： 00 ）才又开始转凉 . 画出这一天 8 ： 00— 20 ： 00 期间气温作为时间函数的一个可能图象，并 说出所画函数的单调区间 . 解： 单调增区间是 [8,12 ） ,[13,18 ） ; 单调减区间是 [12,13 ） ,[18,20]. 【 变式练习 】 作差变形 定号 判断 取值 证明： 根据单调性的定义，设 V 1 , V 2 是定义域 (0,+∞) 上的任意两个实数，且 V 1 < V 2 , 所以，函数 V ∈(0,+∞) 是减函数，也就是说，当体积减小时，压强 p 将增大 . ① 取值： 即设 x 1 、 x 2 是该区间内的任意两个值 , 且 x 1