【数学】江苏省启东中学2019-2020学年高一下学期期中考试试题 8页

江苏省启东中学2019-2020学年高一下学期期中考试试题 一、 单项选择题：本题共8小题，每小题5分，共40分。在每小题给出的四个选项中，‎ 只有一项是符合题目要求的。‎ ‎1. 某学校组织学生参加英语测试，成绩的频率分布直方图如图所示，数据的分组依次为[20,40)，[40,60)，[60,80)，[80,100]．若低于60分的人数是15人，则参加英语测试的学生人数是(　　)‎ A．45 B．‎50 C．55 D．60‎ ‎2. 若以连续掷两枚骰子分别得到的点数m，n作为点P的横、纵坐标，则点P落在 圆x2＋y2＝9内的概率为(　　)‎ A. B. C. D. ‎3. 已知△ABC的三个角A，B，C的对边分别为a，b，c，若＝＝，则该三角形的形状是(　　)‎ A．等腰三角形 B．直角三角形 C．等腰或直角三角形 D．钝角三角形 ‎4. 在△ABC中，AB＝2，AC＝3，·＝1，则BC等于(　　)‎ A. B. C．2 D. ‎5. 过点(0，－2)的直线l与圆x2＋y2＝2x有两个交点，则直线l的斜率k的取值范围是(　　)‎ A. B. C. D. ‎6. 恩格尔系数是食品支出总额占个人消费支出总额的比重. 恩格尔系数越小，即家庭的消费支出中用于购买食物的支出所占比例越小，更多的消费用于精神追求，标志着家庭越富裕. 恩格尔系数达59%以上为贫困，50～59%为温饱，40～50%为小康，30～40%为富裕，低于30%为最富裕。下图给出了1980—2017年我国城镇居民和农村居民家庭恩格尔系数的变化统计图，对所列年份进行分析，则下列结论正确的是（ ）‎ A. 农村和城镇居民家庭消费支出呈下降趋势 B. 农村居民家庭比城镇居民家庭用于购买食品的支出更多 ‎ C. 1995年我国农村居民初步达到小康标准 ‎ D. 2015年城镇和农村居民食品支出占个人消费支出总额之比大于30.6%‎ ‎7. 如图，一座圆弧形拱桥，当水面在如图所示的位置时，拱顶离 ‎ 水面‎2米，水面宽‎12米，当水面下降‎1米后，水面宽度为(　　)‎ A．米　　 B．‎2‎米 C‎.14米 D．‎‎15米 ‎8. 已知锐角三角形ABC的三个内角A，B，C所对的边分别是a，b，c，若a=1，b=3，‎ 则c的取值范围是（ ）‎ A. B. C. D. ‎ 二、 多项选择题：本题共4小题，每小题5分，共20分。在每小题给出的四个选项中，有多项符合题目要求。全部选对的得5分，部分选对的得3分，有选错的得0分。‎ ‎9. 某同学参加社会实践活动，随机调查了某小区5个家庭的年可支配收入x（单位：万元）与年家庭消费y（单位：万元）的数据，制作了对照表：‎ x / 万元 ‎2.7‎ ‎2.8‎ ‎3.1‎ ‎3.5‎ ‎3.9‎ y / 万元 ‎1.4‎ ‎1.5‎ ‎1.6‎ ‎1.8‎ ‎2.2‎ 由表中数据得回归直线方程为，得到下列结论，其中正确的是（ ）‎ A. 若某户年可支配收入4万元为时，则年家庭消费约为2.3万元 ‎ B. 若某户年可支配收入4万元为时，则年家庭消费约为2.1万元 ‎ C. 若年可支配收入每增加1万元，则年家庭消费相应平均增加0.5万元 ‎ D. 若年可支配收入每增加1万元，则年家庭消费相应平均增加0.1万元 ‎ ‎10. 已知A(m,3)，B(‎2m，m＋4)，C(m＋1,2)，D(1,0)，且直线AB与CD平行，则m的值为(　　)‎ A．－1　 B．‎0 C． 1 D．2‎ ‎11. 在△ABC中，角A，B，C的对边分别为a，b，c，若(a2＋c2－b2)tanB＝ac，则B的值为(　　)‎ A．　 B． C． D．‎ ‎12. 已知圆C1：(x－3)2＋(y－4)2＝25与圆C2：(x－1)2＋(y－2)2＝r2(r>0)相内切，则r等于(　　)‎ A．5＋2 B．－5＋2 C．5－2 D．－5－2 三、 填空题：本题共4小题，每小题5分，共20分。请把答案直接填写在答题卡相应的位置上。‎ ‎13. 已知一组数据x1，x2，x3，x4，x5的平均数是2，方差是，那么另一组数据3x1－2,‎ ‎3x2－2,3x3－2,3x4－2,3x5－2的平均数为 ，方差为 .‎ ‎14. 袋中有12个小球，分别为红球、黑球、黄球、绿球，从中任取一球，得到红球概率为， ‎ 得到黑球或黄球概率是，得到黄球或绿球概率是，则任取一球得到黄球的概率为 .‎ ‎15. 在△ABC中，C＝60°，a＋b＝16，则△ABC的周长l的最小值是________。‎ ‎16. 设集合，，若存 在实数，使得，则实数的取值范围是________.‎ 四、 解答题：本题共6小题，共70分。请在答题卡制定区域内作答。解答时应写出文字说明、证明过程或演算步骤。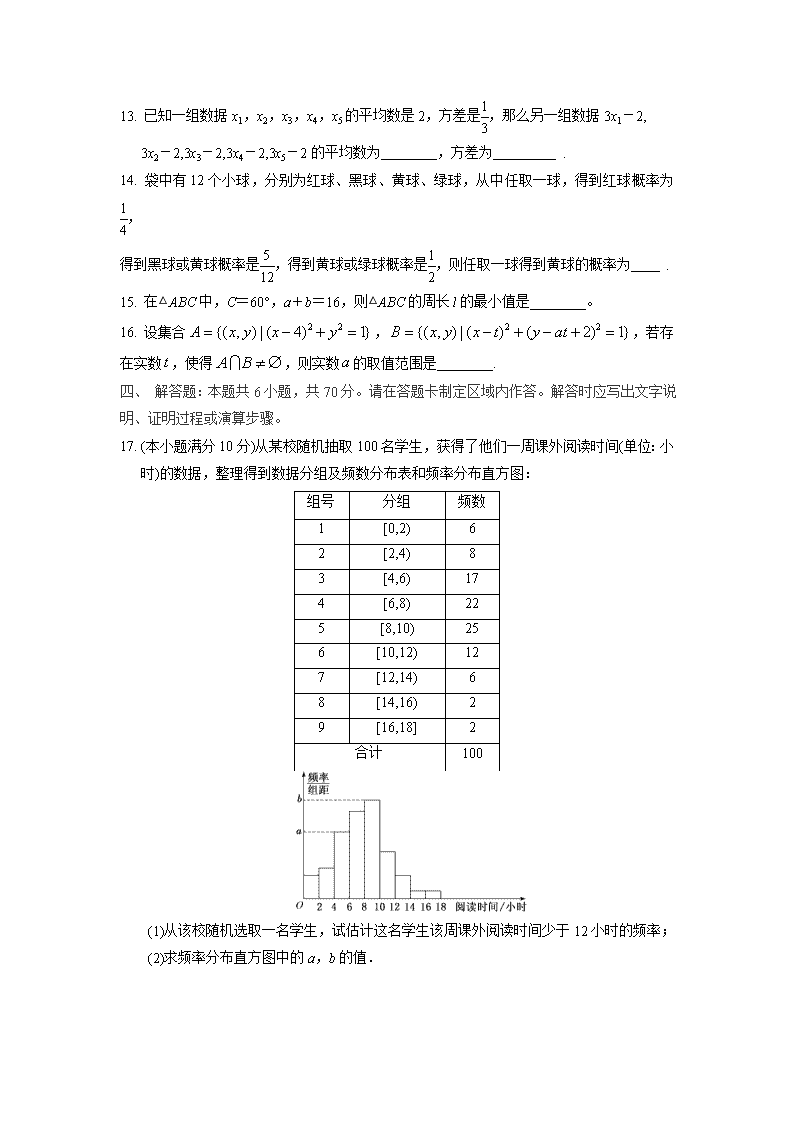‎ ‎17. (本小题满分10分)从某校随机抽取100名学生，获得了他们一周课外阅读时间(单位：小时)的数据，整理得到数据分组及频数分布表和频率分布直方图：‎ 组号 分组 频数 ‎1‎ ‎[0,2)‎ ‎6‎ ‎2‎ ‎[2,4)‎ ‎8‎ ‎3‎ ‎[4,6)‎ ‎17‎ ‎4‎ ‎[6,8)‎ ‎22‎ ‎5‎ ‎[8,10)‎ ‎25‎ ‎6‎ ‎[10,12)‎ ‎12‎ ‎7‎ ‎[12,14)‎ ‎6‎ ‎8‎ ‎[14,16)‎ ‎2‎ ‎9‎ ‎[16,18]‎ ‎2‎ 合计 ‎100‎ ‎(1)从该校随机选取一名学生，试估计这名学生该周课外阅读时间少于12小时的频率；‎ ‎(2)求频率分布直方图中的a，b的值．‎ ‎18. (本小题满分12分)在△ABC中，已知BC＝a，AC＝b，a，b是方程x2－2x＋2＝0的 两根，且2cos(A＋B)＝1，求：‎ ‎(1)C的度数；‎ ‎(2)AB的长度.‎ ‎19. (本小题满分12分)如图，矩形的两条对角线相交于点，边所在直线 的方程为，点在边所在的直线上.‎ ‎(1)求边所在直线的方程；‎ ‎(2)求矩形外接圆的方程．‎ ‎20. (本小题满分12分)如图所示的四边形ABCD中，已知AB⊥AD，∠ABC＝120°，‎ ‎∠ACD＝60°，AD＝27，设∠ACB＝θ，C点到AD的距离为h.‎ ‎(1)用θ表示h的解析式；‎ ‎(2)求AB＋BC的最大值.‎ ‎21. (本小题满分12分)在流行病学调查中，潜伏期指自病原体侵入机体至最早临床症状出现之间的一段时间。某地区一研究团队从该地区500名A病毒患者中，按照年龄是否超过60岁进行分层抽样，抽取50人的相关数据，得到如下表格：‎ 潜伏期（单位：天）‎ ‎[0,2]‎ ‎(2,4]‎ ‎(4,6]‎ ‎(6,8]‎ ‎(8,10]‎ ‎(10,12]‎ ‎(12,14]‎ 人 ‎ 数 ‎60岁及以上 ‎2‎ ‎5‎ ‎8‎ ‎7‎ ‎5‎ ‎2‎ ‎1‎ ‎60岁以下 ‎0‎ ‎2‎ ‎2‎ ‎4‎ ‎9‎ ‎2‎ ‎1‎ ‎（1）估计该地区500名患者中60岁以下的人数；‎ ‎（2）以各组的区间中点值为代表，计算50名患者的平均潜伏期（精确到0.1）；‎ ‎（3）从样本潜伏期超过10天的患者中随机抽取两人，求这两人中恰好一人潜伏期超过12天的概率.‎ ‎22. (本小题满分12分)已知圆M的圆心M在x轴上，半径为，直线l被圆M截得的弦长为，且圆心M在直线l的上方．‎ ‎（1）求圆的方程；‎ ‎（2）设,，若圆M是的内切圆，求AC, BC边所在直线的斜率（用t表示）；‎ ‎（3）在（2）的条件下求的面积S的最大值及对应的t值．‎ 参考答案 ‎1.B ； 2. A； 3. B； 4.A； 5.C； 6.D； 7.B； 8.D；‎ ‎9.BD； 10. BC； 11.AB； 12. AC；‎ ‎13. 4, 3； 14.； 15. 24； 16. ‎ ‎17.解：(1)根据频数分布表知，100名学生中一周课外阅读时间不少于12小时的学生共有6＋2＋2＝10(名)，所以样本中的学生一周课外阅读时间少于12小时的频率是1－＝0.9.‎ ‎(2)课外阅读时间落在[4,6)组内的有17人，频率为0.17，所以a＝＝＝0.085.课外阅读时间落在[8,10)组内的有25人，频率为0.25，所以b＝＝＝0.125.‎ ‎18.解：(1)由2cos(A＋B)＝1，得2cos(π－C)＝1，即cosC＝－，故C＝120°.‎ ‎(2)因为a，b是方程x2－2x＋2＝0的两根，所以a＋b＝2，ab＝2，‎ 所以c2＝a2＋b2－2abcosC＝(a＋b)2－2ab－2abcosC ‎＝(2)2－2×2－2×2×cos120°＝10.‎ 所以AB＝c＝.‎ ‎19.解： (1)因为边所在直线的方程为，且与垂直，‎ 所以直线的斜率为.‎ 又因为点在直线上，所以边所在直线的方程为，‎ 即.‎ ‎(2)由，解得点的坐标为．‎ 因为矩形两条对角线的交点为．‎ 所以为矩形外接圆的圆心．‎ 又|，‎ 从而矩形外接圆的方程为.‎ ‎20.解：(1)由已知，得∠ADC＝360°－(90°＋120°＋60°＋θ)＝90°－θ.‎ 在△ACD中，由＝，得AC＝＝18cosθ.‎ 又∠CAD＝180°－∠ADC－∠ACD＝30°＋θ，且0°<θ<60°，‎ 所以h＝ACsin∠CAD＝18cosθsin(30°＋θ)(0°<θ<60°).‎ ‎(2)在△ABC中，由正弦定理，得AB＝＝18sin2θ，‎ BC＝＝36cosθsin(60°－θ)＝9＋9cos2θ－9sin2θ，‎ 于是AB＋BC＝9＋9cos2θ＋9sin2θ＝9＋18sin(2θ＋60°).‎ 因为0°<θ<60°，所以当θ＝15°时，AB＋BC取得最大值9＋18.‎ ‎21.解：（1）调查的50名A病毒患者中，年龄在60岁以下的有20人，因此该地区A病毒患者中，60岁以下的人数估计有人.‎ ‎（2）（天）‎ ‎（3）样本潜伏期超过10天的患者共六人，其中潜伏期在10~12天的四人编号为：1,2,3,4，潜伏期超过12天的两人编号为：5,6，从六人中抽取两人包括15个基本事件：‎ ‎1,2；1,3； 1,4；1,5；1,6；2,3；2,4；2,5；2,6；3,4；3,5；3,6；4,5；4,6；5,6.‎ 记事件“恰好一人潜伏期超过12天”为事件A，则事件A包括8个，‎ 所以.‎ 答：‎ ‎22.解：（1）设圆心，由已知得到的距离 为,.‎ 又在的上方，，,，故圆的方程为.‎ ‎（2）设斜率为，斜率为，‎ 则直线的方程为，直线的方程为．‎ 由于圆与相切，所以，;同理，.‎ ‎（3）联立两条直线方程得点的横坐标为 ‎ ，‎ 由（2）得：，‎ ‎，，‎ ‎，此时，或.‎ 综上：的面积的最大值为，此时或.‎