2021高考数学新高考版一轮习题：专题7 阶段滚动检测（四） Word版含解析 12页

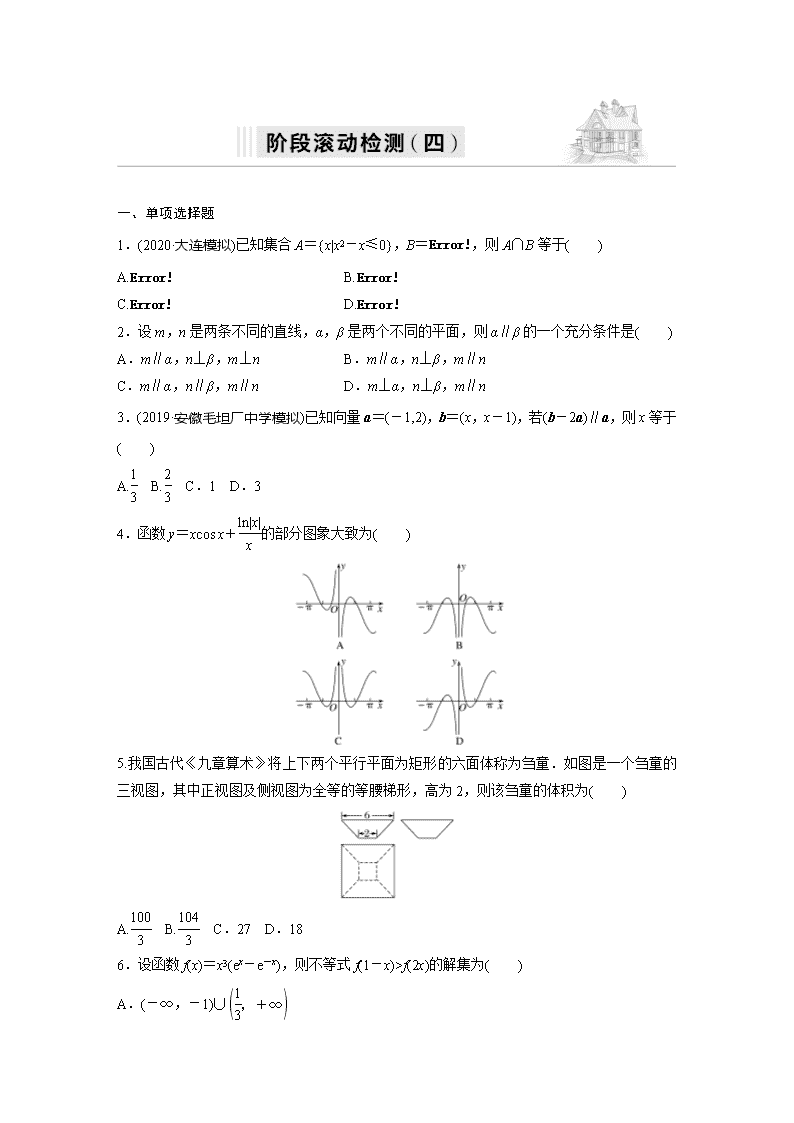
一、单项选择题 ‎1．(2020·大连模拟)已知集合A＝{x|x2－x≤0}，B＝，则A∩B等于(　　)‎ A. B. C. D. ‎2．设m，n是两条不同的直线，α，β是两个不同的平面，则α∥β的一个充分条件是(　　)‎ A．m∥α，n⊥β，m⊥n B．m∥α，n⊥β，m∥n C．m∥α，n∥β，m∥n D．m⊥α，n⊥β，m∥n ‎3．(2019·安徽毛坦厂中学模拟)已知向量a＝(－1,2)，b＝(x，x－1)，若(b－2a)∥a，则x等于(　　)‎ A. B. C．1 D．3‎ ‎4．函数y＝xcos x＋的部分图象大致为(　　)‎ ‎5.我国古代《九章算术》将上下两个平行平面为矩形的六面体称为刍童．如图是一个刍童的三视图，其中正视图及侧视图为全等的等腰梯形，高为2，则该刍童的体积为(　　)‎ A. B. C．27 D．18‎ ‎6．设函数f(x)＝x3(ex－e－x)，则不等式f(1－x)>f(2x)的解集为(　　)‎ A．(－∞，－1)∪ B. C．(－1,0)∪ D. ‎7．已知函数f(x)＝若函数g(x)＝f(x)＋1有三个零点，则实数m的取值范围是(　　)‎ A．(2，＋∞) B．(2,3] C．[2,3) D．(1,3)‎ ‎8．(2020·唐山模拟)已知定义在R上的奇函数f(x)，设其导函数为f′(x)，当x∈(－∞，0]时，恒有xf′(x)F(2x－1)的实数x的取值范围是(　　)‎ A. B．(－1,2) C. D．(－2,1)‎ 二、多项选择题 ‎9．已知a，b为非零实数，且a0 B．q>0‎ C.＝3或－1 D.＝9‎ ‎11.设函数f(x)＝Asin (ωx＋φ)(A，ω，φ是常数，A>0，ω>0)，且函数f(x)的部分图象如图所示，将函数f(x)的图象向右平移个单位长度所得函数图象与g(x)＝Acos(ωx＋α)的图象重合，则下列不符合α的值的是(　　)‎ A．－ B．－ C. D. ‎12.如图，在矩形ABCD中，M为BC的中点，将△AMB沿直线AM翻折成△AB1M，连接B1D，N为B1D的中点，则在翻折过程中，下列说法正确的是(　　)‎ A．存在某个位置，使得CN⊥AB1‎ B．翻折过程中，CN的长是定值 C．若AB＝BM，则AM⊥B1D D．若AB＝BM＝1，当三棱锥B1－AMD的体积最大时，三棱锥B1－AMD的外接球的表面积是4π 三、填空题 ‎13．(2019·宣威市第五中学期中)在△ABC中，内角A，B，C的对边分别是a，b，c，若a＝，c＝，A＝，则△ABC的面积为________．‎ ‎14．在正方体ABCD－A1B1C1D1中，异面直线A1B与AD1所成角的大小为________．‎ ‎15．已知△ABC是边长为2的等边三角形，M为△ABC内部或边界上任意一点，则·的最大值为________，最小值为________．‎ ‎16．(2020·河南南阳中学月考)若二次函数f(x)＝ax2＋bx＋c(a≠0)的图象和直线y＝x无交点，现有下列结论：‎ ‎①方程f(f(x))＝x一定没有实数根；‎ ‎②若a>0，则不等式f(f(x))>x对一切实数x都成立；‎ ‎③若a<0，则必存在实数x0，使f(f(x0))>x0；‎ ‎④若a＋b＋c＝0，则不等式f(f(x))0恒成立；‎ ‎(2)若k∈Z，不等式k(x－1)0，解得x>2.3.‎ ‎∵x∈N，∴x≥3，∴3≤x≤6，且x∈N.‎ 当60，得00，得－10)，‎ 则h′(x)＝－1，‎ 由h′(x)＝－1>0得01，‎ ‎∴h(x)在(0,1)上单调递增，在(1，＋∞)上单调递减，‎ ‎∴h(x)≤h(1)＝0，∴ln x≤x－1，‎ 因此当x>0时，xln x≤x2－x，‎ 即f(x)≤g(x)对x>0恒成立．‎ ‎(2)解　由k(x－1)1)，得k<，‎ 令g(x)＝(x>1)．‎ 则g′(x)＝ ‎＝.‎ 令h(x)＝x－2－ln x，则h′(x)＝1－>0，‎ ‎∴h(x)在(1，＋∞)上单调递增，‎ 又h(3)<0，h(4)>0，故∃x0∈(3,4)，使h(x0)＝0.‎ ‎∴g(x)在(1，x0)上单调递减，在(x0，＋∞)上单调递增，‎ ‎∴g(x)最小为g(x0)＝＝＝x0.‎ ‎∴k的最大值为3.‎