广西南宁三中2020届高考适应性月考卷（五）理科数学试卷 Word版含解析 25页

- 1 - 广西南宁三中 2020 届高考适应性月考卷（五）理科数学 一、选择题（本大题共 12 小题，每小题 5 分，共 60 分.在每小题给出的四个选项 中，只有一项是符合题目要求的） 1. 已知集合  2, 1,0,1A    ，    2 1 0B x x x    ，则 A B  （ ） A.  0,1 B.  -1,0,1 C.  -1,0,1,2 D.  1,0 【答案】B 【解析】 【分析】 化简可得      2 1 0 = 1 2B x x x x x       ，由  2, 1,0,1A    直接求交集即可. 【详解】      2 1 0 = 1 2B x x x x x       ， 由  2, 1,0,1A    ， 所以  1,0,1A B   , 故选：B. 【点睛】本题考查了集合的交集运算，考查了一元二次不等式的计算，属于基础题. 2. 设 i 是虚数单位，若复数 z 满足 ( 1) 1z i i   ，则其共轭复数 z  （ ） A. i B. i C. 1 i  D. 1 i  【答案】A 【解析】 【分析】 首先根据题中所给的式子，利用复数除法运算求得 z i  ，再根据共轭复数的定义求得结果. 【详解】由题得 21 (1 ) 2 1 ( 1)( 1) 2 i i iz ii i i          ， 所以 z i ， 故选：A. 【点睛】本题主要考查复数的除法运算和共轭复数的概念，意在考查学生对这些知识的理解 掌握水平. 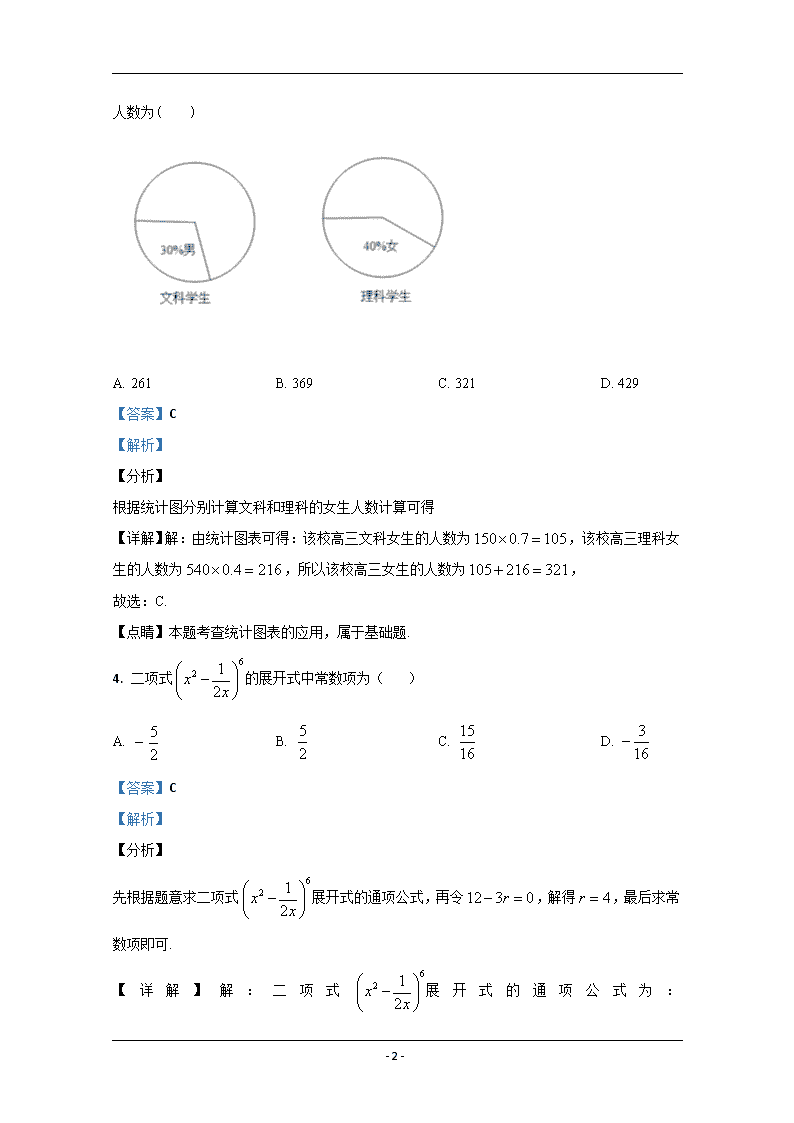3. 某校高三有文科学生 150 名，理科学生 540 名，其性别比例如图所示，则该校高三女生的 - 2 - 人数为( ) A. 261 B. 369 C. 321 D. 429 【答案】C 【解析】 【分析】 根据统计图分别计算文科和理科的女生人数计算可得 【详解】解：由统计图表可得：该校高三文科女生的人数为150 0.7 105  ，该校高三理科女 生的人数为540 0.4 216  ，所以该校高三女生的人数为105 216 321  ， 故选：C. 【点睛】本题考查统计图表的应用，属于基础题. 4. 二项式 6 2 1 2x x     的展开式中常数项为（ ） A. 5 2  B. 5 2 C. 15 16 D. 3 16  【答案】C 【解析】 【分析】 先根据题意求二项式 6 2 1 2x x     展开式的通项公式，再令12 3 0r  ，解得 4r  ，最后求常 数项即可. 【 详 解 】 解 ： 二 项 式 6 2 1 2x x     展 开 式 的 通 项 公 式 为 ： - 3 -  62 12 3 1 6 6 1 2 1 2 rr r r r r rT C x C xx               ， 令12 3 0r  ，解得 4r  ， 所以常数项 5 6 4 4 15 6 1 12T C       故选：C. 【点睛】本题考查求二项式展开式的常数项，是基础题. 5. 已知 1sin cos 2    ，则 2cos 4      （ ） A. 7 16 B. 7 8 C. 5 4 D. 7 4 【答案】B 【解析】 【分析】 由同角三角函数的平方关系、二倍角公式可得 3sin2 4   ，再由降幂公式、诱导公式可得 2 1 sin2cos 4 2        ，即可得解. 【详解】由 1sin cos 2    两边平方得： 2 2 1sin 2sin cos cos 4       ， 所以 32sin cos 4    即 3sin2 4   ， 所以 2 1 cos 2 1 sin2 72cos 4 2 2 8                . 故选：B. 【点睛】本题考查了同角三角函数的平方关系、诱导公式及二倍角公式的综合应用，考查了 运算求解能力，属于基础题. 6. 函数 31( ) ln3f x x a x  的图象在 (1, (1))f 处的切线方程为 6 3 0x y b   ，则 a b  （ ） A. 3 B. 4 C. 5 D. 6 【答案】D - 4 - 【解析】 【分析】 先求得切点坐标，对函数求导后利用导数的几何意义求得切线的斜率，然后利用直线的点斜 式方程即可求得切线方程，从而求得 ,a b 的值，从而求得结果. 【详解】因为 31( ) ln3f x x a x  ， 当 1x  时， 1(1) 3f  ，故切点为 11, 3      . 所以 2( ) af x x x    ， 则斜率 (1) 1k f a   ， 所以切线方程为 1 (1 )( 1)3y a x    ， 又因为切线方程为： 6 3 0x y b   ， 比较系数知 1a  ， 5b  ， 所以 a b  6. 故选：D. 【点睛】本题主要考查导数的几何意义的应用，考查了学生的数学运算能力，属基础题. 7. 运行如图所示的程序算法，则输出的结果为( ) A. 2 B. 1 2 C. 13 D. 13 2 【答案】A 【解析】 - 5 - 【分析】 根据框图的流程模拟运行程序，得到 a 的值出现的周期，根据条件确定跳出循环的 k 值，从而 确定结果. 【详解】当 2a  时， 1k  ；当 13 2a  时， 3k  ； 当 13 213 2 a   时， 5k  ；…；当 13 2a  时， 99k  ， 当 2a  时， 101k  ，跳出循环； 故选:A. 【点睛】本题主要考查了循环结构的程序框图，根据框图的流程模拟运行程序发现 a 值出现的 周期性的变化是解题的关键，属于基础题. 8. 已知函数  f x 的部分图象大致如图，则  f x 的解析式可能是( ) A.   2 1 cos2 1 x x xf x   B.   sin x x xf ex e  C.   1 cosf x xx x      D.   1 sin1 x x ef x xe   【答案】D 【解析】 【分析】 根据图象的对称性可以排除 A,C，结合在点 0x  附近的变化趋势可得 D 选项为正确答案. 【详解】由图象观察可知，函数图象关于 y 轴对称， 对于选项 A，  2 1 1 2( ) cos cos ( )2 1 1 2 x x x xf x x x f x             ，故为奇函数，不合题意； 对于选项 C，  1 1( ) cos cos ( )f x x x x x f xx x                    ，故为奇函数，不合题 - 6 - 意；对于选项 B，当 0x  ，且 0x  时，   0f x  ，故排除 B. 故选：D. 【点睛】本题主要考查函数图象的识别，由图选式，一般通过图象的性质进行排除，侧重考 查直观想象的核心素养. 9. 如图，已知多面体 1 1 1 1ABCD A B C D 是正方体，E ，F 分别是棱 1AA ， 1CC 的中点，点 M 是棱 1BB 上的动点，过点 E ，M ，F 的平面与棱 1DD 交于点 N ，则以下说法不正确的是( ) A. 四边形 EMFN 是平行四边形 B. 四边形 EMFN 是菱形 C. 当点 N 从点 1D 往点 D 运动时，四边形 EMFN 的面积先增大后减小 D. 当点 N 从点 1D 往点 D 运动时，三棱锥 1D EFN 的体积一直增大 【答案】C 【解析】 【分析】 对选项逐一判断，可得答案. A 项，由面面平行的性质定理可得 // , //EN MF EM NF ，故四边 形 EMFN 是平行四边形. B 项，由 1 1 1 1ABCD A B C D 是正方体，易知 AC  平面 1 1BDD B ， //EF AC ，故 EF  平面 1 1BDD B ，故 EF MN ，故平行四边形 EMFN 是菱形.C 项，菱形 EMFN 的面积 1 2S EF MN  ，线段 EF 的长度是定值，菱形 EMFN 的面积先减小后增大. D 项，由 1 1D EFN F D ENV V  ，点 F 到平面 1 1ADD A 的距离不变，当点 N 从点 1D 往点 D 运动时， 三角形 1D EN 的面积一直增大，故三棱锥 1D EFN 的体积一直增大. 【详解】如图所示 - 7 - 平面 1 1 //ADD A 平面 1 1BCC B ，平面 EMFN  平面 1 1ADD A EN ， 平面 EMFN  平面 1 1BCC B MF ， //EN MF ，同理 //EM NF ， 四边形 EMFN 是平行四边形，故 A 正确. 1 1 1 1ABCD A B C D 是正方体， AC BD  ，又 1BB  平面 ABCD ， 1BB AC  ， 1BB BD B  ， AC  平面 1 1BDD B . ,E F 分别是棱 1 1,AA CC 的中点， //EF AC ， EF  平面 1 1BDD B ， 又 MN  平面 1 1BDD B ， EF MN  ，平行四边形 EMFN 是菱形，故 B 正确. 菱形 EMFN 的面积 1 2S EF MN  ，线段 EF 的长度是定值.当点 N 从点 1D 往点 D 运动时， 线段 NM 的长度先减小后增大，菱形 EMFN 的面积先减小后增大，故C 不正确. 1 1D EFN F D ENV V  ，点 F 到平面 1 1ADD A 的距离不变.当点 N 从点 1D 往点 D 运动时，三角形 1D EN 的面积一直增大，三棱锥 1D EFN 的体积一直增大，故 D 正确. 故选：C . 【点睛】本题考查面面平行的性质定理、线面垂直的判定定理和求三棱锥体积的方法，属于 中档题. 10. 已知l 为抛物线 2 8x y 的准线，抛物线上的点 A 到l 的距离为 d ，M 点的坐标为 8,2 ， 则 AM d 的最小值为( ) A. 4 B. 8 C. 16 D. 2 2 【答案】B 【解析】 【分析】 - 8 - 由抛物线方程可知，抛物线的焦点 F 和准线 l ，过 A 作准线的垂线，由抛物线的定义知 AF d ，然后利用垂线段最短，连接 M F 即为所求. 【详解】如图所示： 抛物线的焦点为  0,2F ，准线为 l : 2 y ， 过 A 作 AN 交l 于点 N ，连接 AF ， 由抛物线的定义得 AF AN d  ， ∴ 8AM d AM AF MF     ， 当且仅当 M ， A ， F 三点共线时取“  ”号， ∴ AM d 的最小值为 8. 故选：B. 【点睛】本题主要考查抛物线的定义以及线段和最小问题，还考查了数形结合的思想方法， 属于中档题. 11. 定义在 R 上的奇函数满足 ( 2) (2 )f x f x    ，当 (0,1)x 时， 4( ) log ( 1)f x x  ， 则 ( )f x 在 (3,4) 上（ ） A. 是减函数，且 ( ) 0f x  B. 是增函数，且 ( ) 0f x  C. 是减函数，且 ( ) 0f x  D. 是增函数，且 ( ) 0f x  【答案】B 【解析】 【分析】 根据函数是奇函数结合对称性求得函数周期；结合对数型复合函数的单调性，以及函数值的 正负，即可判断. - 9 - 【详解】定义在 R 上的奇函数满足 ( 2) (2 )f x f x    ， ∴ ( 2) (2 ) ( 2)f x f x f x      ， ∴ ( 4) ( )f x f x  ，即函数周期是 4. ( )f x 在 (3,4) 上的图象和在 ( 1,0) 上的图象相同， 当 (0,1)x 时， 4( ) log ( 1)f x x  ， ∴此时 ( )f x 单调递增，且 ( ) 0f x  . ∵ ( )f x 是奇函数， ∴当 ( 1,0)x  时， ( )f x 单调递增，且 ( ) 0f x  ， 即当 (3,4)x 时， ( )f x 单调递增，且 ( ) 0f x  ， 故选：B. 【点睛】本题考查函数奇偶性、周期性的应用，涉及对数型复合函数的单调性，属综合基础 题. 12. 已知函数   sin 3 cosf x x x   （ 0 ，xR ），若函数  f x 在区间 ,2  内 没有零点，则 的取值范围是( ) A. 1 2,3 3      B. 1 7,6 12      C. 1 2 1, 0,3 3 6          D. 1 7 1, 0,6 12 12          【答案】C 【解析】 【分析】 先化简  f x ，求出  f x 的零点，使其零点不在区间 ,2  内，根据不等关系可求答案. 【详解】   sin 3 cos 2sin 3f x x x x          ， 令 2sin 03x      ，得 3x k   ， k Z ，即 3k x     ， - 10 - 因为函数  f x 在区间 ,2  内没有零点， 所以 3k x      且 4 3 2 k     ，解得 1 2 3 3 2 kk     ， k Z ， 令 0k  可得 1 2 3 3   ，令 1k   可得 2 1 3 6    ，因为 0 ，所以 的取值范围是 1 2 1, 0,3 3 6          . 故选：C 【点睛】本题主要考查三角函数的性质，把函数化简为最简形式，表示出零点是解题的关键， 侧重考查数学运算的核心素养. 二、填空题（本大题共 4 小题，每小题 5 分，共 20 分） 13. 已知向量  1,2a  r ，  3,4b  ，则 a  在b  方向上的投影为______. 【答案】 11 5 【解析】 【分析】 设 a  与 b  的夹角为  ，利用平面向量数量积的坐标运算可求得 a  在 b  方向上的投影为 cos a ba b      ，即可得解. 【 详 解 】 设 a  与 b  的 夹 角 为  ， 所 以 ， a  在 b  方 向 上 的 投 影 为 2 2 1 2 3 4 11cos 53 4 a ba b            . 故答案为：11 5 . 【点睛】本题考查平面向量投影的计算，涉及平面向量数量积的坐标运算，考查计算能力， 属于基础题. 14. 函数 ( ) sin cosf x x x  ， ,2 2x       的值域为______. 【答案】[ 2,1] 【解析】 - 11 - 【分析】 利用辅助角公式化简函数解析式可得 ( ) 2 sin 4f x x      ,利用正弦函数的图象和性质即 可得解 【详解】 2 2( ) sin cos 2 sin cos2 2f x x x x x         2 sin 4x      . 由于 2 2x    ，所以 3 4 4 4x      ， 所以 21 sin 4 2x        ， 所以 2 2 sin 14x        ， 即 ( )f x 的值域为：[ 2,1] . 故答案为：[ 2,1] 【点睛】本题主要考查了两角差的正弦函数公式，特殊角的三角函数值在三角函数化简中的 应用，考查了正弦函数的图象和性质，属于基础题． 15. 设 1F 、 2F 为双曲线 2 2: 13 yC x   的两个焦点，P 为C 上一点且在第一象限，若 1 2PF F△ 为等腰三角形，则 P 点的坐标为______. 【答案】 3 15,2 2       或 5 3 7,2 2       【解析】 【分析】 根据双曲线方程求得 c ，结合 1 2PF F△ 为等腰三角形以及双曲线的定义列方程组，解方程组求 得 P 点的坐标. 【详解】设 1F 、 2F 分别为双曲线C 的左、右焦点，根据题意可知 1 3 2c    . 因为 1 2PF F△ 为等腰三角形，所以易知 1 1 2 4PF F F  或者是 2 1 2 4PF F F  ， - 12 - 如图分两种情况讨论： 因为 1 2 2 2PF PF a   ，所以 2 4 2 2PF    或者 1 4 2 6PF    . ①若 2 2PF  ，设点  ,P x y ， 则   2 2 22 2 2 13 2 4 0 0 yx PF x y x y             ，解得 3 2 15 2 x y     ，即点 3 15,2 2P       ； ②若 1 6PF  ， 则   2 2 22 2 1 13 2 36 0 0 yx PF x y x y             ，解得 5 2 3 7 2 x y     ，即点 5 3 7,2 2P       . 综上所述，点 P 的坐标为 3 15,2 2       或 5 3 7,2 2       . 故答案为： 3 15,2 2       或 5 3 7,2 2       . 【点睛】本题主要考查双曲线定义，考查数形结合的数学思想方法，属于中档题. - 13 - 16. 某顶部有盖的几何体容器的三视图如图所示，网格纸上小正方形的边长为 1，若在该几何 体内部放入一个小圆柱体，且小圆柱体的上下底面均与顶部圆盖所在平面平行，则小圆柱体 积的最大值为______. 【答案】 32 27  【解析】 【分析】 设 小 圆 柱 体 的 底 面 半 径 为 cos ， 则 高 为 1 sin ， 0, 2      ， 小 圆 柱 体 的 体 积  2cos 1 sinV       ，设sin t  ，  0,1t  ，再利用导数求最值，即可得到答案； 【详解】如图，设小圆柱体的底面半径为 cos ，则高为1 sin ， 0, 2      ， 则小圆柱体的体积  2cos 1 sinV       ，设sin t  ，  0,1t  ， 则     2 3 21 1 1V t t t t t           ， 则     23 2 1 3 1 1V t t t t            ，当 1 3t  时， max 32 27V  . 故答案为： 32 27  【点睛】本题考查圆柱体积的最大值求法，考查空间想象能力、运算求解能力，求解时注意 借助导数求最值. - 14 - 三、解答题（共 70 分.解答应写出文字说明，证明过程或演算步骤） 17. 等差数列 na 的前 n 项和为 nS ， 3 3a  ，其中 1 3 9, ,a a a 成等比数列，且数列 na 为非常 数数列. （1）求数列通项 na ； （2）设 1 n n b S  ， nb 的前 n 项和记为 nT ，求证： 2nT  . 【答案】（1） na n ；（2）证明见解析. 【解析】 【分析】 （1）由已知条件列出关于公差的方程求解即可得到通项公式； （2）由（1）求得 nS 得到 nb ，利用裂项求和法求出 nT 即可证明. 【详解】解：（1）因为 1 3 9, ,a a a 成等比数列，所以 2 3 1 9a a a ， 即   23 3 2 3 6d d   ， 解得 1d  或 0d  （舍去），所以  3 3 1na a n n     . （2）由（1）知：     1 1 1 2 2n n n n nS na d      .则   1 2 1 121 1n n b S n n n n         ， 1 2 1 1 1 1 1 1 12 2 1 21 2 2 3 1 1n nT b b b n n n                          . 【点睛】本题主要考查等比中项、等差数列的通项公式和前 n 项和公式以及裂项相消法求和， 还考查了运算求解的能力，属于中档题. 18. 为了了解市民对电视剧市场的爱好，某上星电视台邀请了 100 位电视剧爱好者（男 50 人、 女 50 人）对 4 月份观看其播出的电视剧集数进行调研，得到这 100 名电视剧爱好者观看集数 的中位数为 39 集（假设这 100 名电视剧爱好者的观看集数均在 25,55 集内），且观看集数在  45,50 集内的人数为 15，并根据调查结果画出如图所示的频率分布直方图. - 15 - （1）求 m ， n 的值； （2）有些观众喜欢带有主角光环意识来观剧.但是最近几年的影视作品里出现了一个有趣的趋 势——攻气十足的女性角色越来越讨人喜欢，傻白甜的女主们则破了主角光环，各种被嫌弃， 更有些剧集中明明是女配的脚本，却因为更具有大女主气场，而获得了比主角更多的关注与 声量，如《完美关系》里的斯黛拉，《精英律师》里的栗娜，《我的前半生》里的唐晶，…… 已知在这 100 名电视剧爱好者的女性中有 31 名认为自己有主角光环意识，男性中有 19 名认 为自己有主角光环意识，根据以上数据请同学们制作出列联表，并且判断能否在犯错误的概 率不超过 0.001 的前提下认为性别与是否观剧带有主角光环意识有关系？ 参考公式及数据：        2 2 n ad bcK a b c d a c b d      ，其中 n a b c d    . P （ 2 0K k ） 0.05 0.01 0.005 0.001 0k 3.841 6.635 7.879 10.828 【答案】（1） 0.02m  ， 0.025n  ；（2）列联表见解析，不能. 【解析】 【分析】 （1）根据观看集数在 45,50 集内的人数求得对应的频率，利用频率之和为1，以及中位数列 方程，解方程求得 ,m n 的值. （2）根据已知条件填写 2 2 列联表，计算出 2K 的值，由此判断出不能在犯错误的概率不超 过 0.001的前提下认为性别与是否观剧带有主角光环意识有关系. - 16 - 【详解】（1）∵观看集数在 45,50 内的人数为 15， ∴观看集数在 45,50 内的频率为 15 0.15100  ； 由频率分布直方图得 0.02 2 4 0.01 5 0.15 1m n      ，化简得 2 0.07m n  ，① 由中位数可得  0.02 5 2 5 2 39 35 0.5m n       ，化简得 5 4 0.2m n  ，② 由①②解得 0.02m  ， 0.025n  . （2）根据题意得到列联表： 男 女 总计 观剧有主角光环意识 19 31 50 观剧没有主角光环意识 31 19 50 总计 50 50 100 ∴  2 2 100 19 19 31 31 5.76 10.82850 50 50 50K         ， ∴不能在犯错误的概率不超过 0.001 的前提下认为性别与是否观剧带有主角光环意识有关系. 【点睛】本小题主要考查频率分布直方图，考查 2 2 列联表独立性检验，属于中档题. 19. 两个边长均为 2 的正方形 ABCD 与 ABEF 按如图的位置放置，M 为 BD 的中点，   0,1FP FB    . （1）当 1 2   时，证明： //MP 平面 BCE ； （2）若 D 在平面 ABEF 上的射影为 AF 的中点， MP 与平面 ABCD 所成角为 30°，求  的 值. - 17 - 【答案】（1）见详解；（2） 7 17 4  . 【解析】 【分析】 （1）根据题意证明平面 PMN ∥平面 BCE ，即可得证； （2）连接 DF ， 由题意可得 2DF  ，由 BDF 中可得，根据 MP 与平面 ABCD 所成角为 30°，可得 2 3(1 )MP   ，由因为 2 2(1 )BP   ， 2MB  ，再结合 2 2 2 8 8 4 12 3cos 2 16 42 2 2 2 2 BD BF DFDBF BD BF           ，在AMP 中由余弦定理 代入 2 2 2 2 cosMP MB BP MP BP MBP     即可得解. 【详解】（1） 如图，作 AB 中点 N ，连接 MN ， PN ， 由 1 2   ，所以 P 为 FB 中点， 所以 NP ∥ AF ∥ BE ，又 NP  平面 BCE ， 所以 NP ∥平面 BCE ， 同理可得 MN ∥平面 BCE ， 又因为 MN NP N  ， 所以平面 PMN ∥平面 BCE ， 又 MP  平面 PMN ，所以 //MP 平面 BCE . - 18 - （2）如图：连接 DF ，作 AF 中点 Q ，则 Q 为 D 在平面 ABEF 上的投影， 即 DQ  平面 ABEF ，所以 DQ AF ，又 2AD AF  ， 则 ADF 为等边三角形，所以 2DF  ， BDF 中， 2 2 2 8 8 4 12 3cos 2 16 42 2 2 2 2 BD BF DFDBF BD BF           ， 由正方形 ABCD 与 ABEF ，所以 ,AB AF AB AD  ， 所以 AB  平面 ADF ，所以平面 ABCD  平面 ADF ， 作 FI AD 于 I ，则 I 为 AD 中点，且 FI  平面 ABCD 连接 BI ，在 BI 上取 H ,使得 //PH FI ， 则 PH  平面 ABCD ，连接 MH ，则 PMH 为 MP 与平面 ABCD 所成角为 30°， 由   0,1FP FB    ，可得 (1 ) 3(1 )PH FI     ， 所以 2 3(1 )MP   ，又由 2 2(1 )BP   ， 2MB  ， 在AMP 中，由余弦定理可得： 2 2 2 2 cosMP MB BP MP BP MBP     代入可得： 22(1 ) 3(1 ) 1 0      ， 由  0,1  ，解得： 7 17 4   . 【点睛】本题考查了线面垂直的证明以及投影的概念，考查了通过面面垂直正线面垂直，考 查了余弦定理在立体几何中的应用，有一定的计算量，属于中档题. 20. 函数 2(sin cos )( ) ex x xf x  . （1）讨论 ( )f x 在[0, ) 上的最大值； - 19 - （2）有几个 （ 0 ，且为常数），使得函数 ( )y f x 在 0, 2      上的最大值为 2e   ？ 【答案】（1） 2 2 e  ；（2）两个. 【解析】 【分析】 （1）利用导数求 出 ( )f x 在 30, 2      上的最大值为 2 2 2f e       ，然后当 3 2x  时， 2sin 2cos 2 2x x  ， 3 2xe e   ，   3 2 2 2 2 2f x e e    ，从而可得到答案； （2）当 0, 2x      时， 0, 2x       ，然后分 1  、0 1  两种情况讨论，当 0 1  时， 22 e f        ，记 2 sin cos( ) t t t tg t e e     ，利用导数得到 ( )g t 在 0, 2      上有唯一的 零点即可. 【详解】（1） 4cos( ) x xf x e   ， xR ， 当 0, 2x      时， ( ) 0f x  ，单调递增； 当 3,2 2x      时， ( ) 0f x  ， ( )f x 单调递减， ∴ ( )f x 在 30, 2      上的最大值为 2 2 2f e       ； 又当 3 2x  时， 2sin 2cos 2 2x x  ， 3 2xe e   ， 此时   3 2 2 2 2 2f x e e    ， 所以 ( )f x 在[0, ) 上的最大值为 2 2 e  . （2）当 0, 2x      时， 0, 2x       . - 20 - ①当 1  时， 2 2   ，  f x 的最大值为 2 2 e  ， ∴ 2 2 2 e e    ， 2  ； ②当 0 1  时，  f x 的最大值为 2f      ，∴ 22 e f        . 令 0,2 2t       ，则有 2 sin cos t t t t e e     ， 记 2 sin cos( ) t t t tg t e e     ， 则   2 2cos 1 t tg t e e     ， 2(sin cos )( ) t t tg t e    . 当 0, 2t     时， ( ) 0g t  ， ( )g t 单调递减，又∵ 02g      ， ∴ ( )g t 在 0, 2      上有唯一的零点t t 0 . 当  00,t t 时， ( ) 0g t  ， ( )g t 单调递增； 当 0 , 2t t     时， ( ) 0g t  ， ( )g t 单调递减. ∴  0 2 1 02 2 g t g e        ，又∵ (0) 1 0g    ， 所以 ( )g t 在 00,t 上有唯一的零点 1t t ，在 0 , 2t     上的函数值恒大于 0. 即 ( )g t 在 0, 2      上有唯一的零点 1t t . ∴ 2 2f e       在 (0,1)  上有唯一解， 1 1 2t  . 综上所述，有两个 符合题意. 【点睛】本题主要考查导数与函数的单调性，导数与函数的最值，还考查了分类讨论的思想 - 21 - 和运算求解的能力，属于较难题. 21. 如图，椭圆Q ： 2 2 2 2 1x y a b   （ 0a b  ）的离心率 1 2e  ，左、右焦点分别为 1F ， 2F ， 过 1F ， 2F 分别作两条相互垂直的直线 1l ， 2l ，分别交椭圆Q 于 A ，C ， ,B D 四点， 1l ， 2l 的 交点为 M ，三角形 1 2MF F 面积的最大值为 1. （1）求椭圆Q 的方程； （2）当四边形 ABCD 的面积 S 最小时，求点 M 的坐标. 【答案】（1） 2 2 14 3 x y  ；（2） (0,1)M 或 (0, 1) . 【解析】 【分析】 （ 1 ） 由 已 知 可 得 2 2 2 1 2 4MF MF c  ， 根 据 面 积 公 式 及 基 本 不 等 式 可 得  2 2 2 1 2 1 2 1 1 2 4MFFS MF MF MF MF   ，计算求得 1c  ，进而可得 ,a b 即可得出结果； （2）设直线 1l ： 1x my  ，则直线 2l ： 1 1x ym    ，分别与椭圆方程联立，根据弦长公 式及韦达定理化简可得 2 2 2 2 1 1 1| || | 722 4 3 4 3 m mS AC BD m m       ，令 2 1m t  ，化简可得 2 72 1 1 49 2 4 S t        ，根据二次函数性质可知 2t  ，进而得出 m ，通过直线方程联立可求 得交点坐标. 【详解】（1）∵ 1 2l l ，∴ 1 2MF MF ， 设 1( ,0)F c ， 2 ( ,0)F c ，则 2 2 2 1 2 4MF MF c  ， - 22 -  2 2 2 2 1 2 1 2 1 1 2 4MFFS MF MF MF MF c    ‖ ， 当且仅当 1 2 2MF MF c  时取得最大值 2c ，∴ 2 1c  ， 1c  ， ∵椭圆Q 的离心率 1 2 ce a   ，∴ 2a  ， 又由 2 2 2 3b a c   ，∴椭圆Q 的方程为 2 2 14 3 x y  . （2）由椭圆的对称性知，斜率为 0 时和斜率不存在是面积一样， 设直线 1l ： 1x my  ，由   2 2 2 21, 4 3 6 9 04 3 1 x y m y my x my            ， 设  1 1,A x y ，  2 2,C x y ，则 1 2 2 6 4 3 my y m    ， 1 2 2 9 4 3y y m   ，    2 2 2 2 2 1 2 2 2 36 36 4 3 12 1 | | 1 1 4 3 4 3 m m m AC m y y m m m            ， 若 0m  ，| | 3AC  ，这时| | 4BD  ， 1 4 3 62S     ， 若 0m  ，则直线 2l ： 1 1x ym    ， 由 2 2 2 2 1, 3 64 3 4 9 0 1 1 x y y ym mx ym                ， 同理得  22 2 2 112 1 12 1 | | 3 4 34 mmBD m m        ， ∴    2 2 2 2 2 2 2 2 12 1 12 11 1 1 1| | 722 2 4 3 4 3 4 3 4 3 m m m mS AC BD m m m m              ‖ . 设 2 1m t  ，则 2 1m t  （ 1t  ）， 2 1 7272 72 1 13 1 4 1 1 1 493 4 2 4 t tS t t t t t                         ， 当 2t  时， 288 649S   ，∴ min 288 49S  ， - 23 - 这时 2 1m  ， 1m   ， 当 1m  时， 1l ： 1x y  ， 2l ： 1x y   ， 由 1 0 1 1 x y x x y y         当 1m   时， 1l ： 1x y   ， 2l ： 1x y  ， 由 1 0 1 1 x y x x y y          故当 S 最小时，点 M 的坐标为 (0,1)M 或 (0, 1) . 【点睛】本题考查直线和椭圆的关系，考查韦达定理的应用和弦长公式，考查基本不等式及 二次函数在求最值中的应用，属于综合题，难度较难. 22. 在直角坐标系 xOy 中，曲线C 的参数方程为 10 cos 8 10 sin x a y a         （ 为参数，常数 10a  ）.以坐标原点为极点，x 轴的正半轴为极轴建立极坐标系，已知直线 l 的极坐标方程为 sin 2 24       . （1）写出 1C 及直线 l 的直角坐标方程，并指出 1C 是什么曲线； （2）设 A 是曲线 1C 上的一个动点，求点 A 到直线 l 的距离的最小值. 【答案】（1）  22 8 10x y a    ， 4 0x y   ， 1C 表示以 0,8 为圆心， 10 a 为半 径的圆；（2） 2 2 10 a  . 【解析】 【分析】 (1)消去参数 ，即得 1C 的直角坐标方程，利用 cosx   ， siny   ，可将直线方程化 为普通方程； （2）计算点到直线的距离，再讨论直线与曲线的位置关系，即可得到答案； 【详解】（1）消去参数 ，即得 1C 的直角坐标方程为  22 8 10x y a    ， 所以，当 10a  时， 1C 表示以 0,8 为圆心， 10 a 为半径的圆. - 24 - 因为 sin 2 24       ， 所以 sin cos 4     . 因为 cosx   ， siny   ， 所以直线 l 的直角坐标方程为 4y x  ，即 4 0x y   . （2）圆心  0,8C 到直线 l 的距离为  22 0 8 4 2 2 1 1 d      ， 若 d r ，即 2a  ，圆 1C 与直线 l 相交，点 A 到直线l 的距离的最小值为 0， 若 d r ，即10 2a  时，则点 A 到直线l 的距离的最小值为 2 2 10 a  . 综上所述，当 2a  时，圆 1C 与直线 l 相交，点 A 到直线 l 的距离的最小值为 0； 当10 2a  时，则点 A 到直线l 的距离的最小值为 2 2 10 a  . 【点睛】本题考查参数方程、普通方程、极坐标方程的互化、点到直线距离公式的应用，考 查函数与方程思想、转化与化归思想，考查逻辑推理能力、运算求解能力. 23. 已知    0, 0f x x a x b a b      . （1）当 2a  ， 1b  时，解不等式   9f x  ； （2）若  f x 的最小值为 2，求 1 1 1 2a b  的最小值. 【答案】（1）   , 4 5,    ；（2） 1 2 2 3  . 【解析】 【分析】 （1）当 2a  ， 1b  时，   2 1 9f x x x     ， 分类讨论即可得解； （2）由绝对值三角不等式可得  f x x a x b x b x a a b a b            ， 若  f x 的最小值为 2，则 2a b  ，所以 ( 1) 3a b   ，再利用基本不等式即可求最小值. 【详解】（1）当 2a  ， 1b  时，   2 1 9f x x x     ， - 25 - 所以 1 2 1 9 x x      或 1 2 3 9 x     或 2 2 1 9 x x     ， 解得： 4x   或 5x≥ ， 故解集为   , 4 5,    ； （2）由 0, 0a b  ， 所以  f x x a x b x b x a a b a b            ， 若  f x 的最小值为 2，则 2a b  ，所以 ( 1) 3a b   ， 1 1 1 1 1 1 3 1 1 3 1 1 3 1 2( )(( 1) ) ( ) ( 2 ) ( 2)1 2 3 1 2 3 2 1 2 3 2 2 3 2 2 3 b aa ba b a b a b                 ， 所以 1 1 1 2a b  的最小值为 1 2 2 3  . 【点睛】本题考查了解绝对值不等式，考查了绝对值三角不等式以及基本不等式的应用，考 查了分类讨论思想，属于基础题.