山东省潍坊市2019-2020学年高一下学期期末考试数学试题 26页

高一数学 一、单项选择题：本题共8小题，每小题5分，共40分.在每小题给出的四个选项中，只有一项是符合题目要求的.‎ ‎1. 设为虚数单位，则复数（ ）‎ A. B. C. D. ‎ ‎【答案】B ‎【解析】‎ ‎【分析】‎ 首先将分子的1化为，然后约分化简.‎ ‎【详解】因为，‎ 故选：B ‎【点睛】本题主要考查了复数代数形式的运算，虚数单位的性质，属于容易题.‎ ‎2. （ ）‎ A. B. C. D. ‎ ‎【答案】D ‎【解析】‎ ‎,‎ 故选D ‎3. 已知某扇形的半径为，圆心角为，则此扇形的面积为（ ）‎ - 26 -‎ A. B. C. D. ‎ ‎【答案】B ‎【解析】‎ ‎【分析】‎ 根据扇形的面积公式，即可求得此扇形的面积，得到答案.‎ ‎【详解】由题意，某扇形的半径为，圆心角为，‎ 根据扇形的面积公式，可得 ‎ 所以此扇形的面积为.‎ 故选：B.‎ ‎【点睛】本题主要考查了扇形的面积公式及其应用，其中解答中熟记扇形的面积公式是解答的关键，着重考查推理与运算能力.‎ ‎4. 在中，点满足，则（ ）‎ A. B. ‎ C. D. 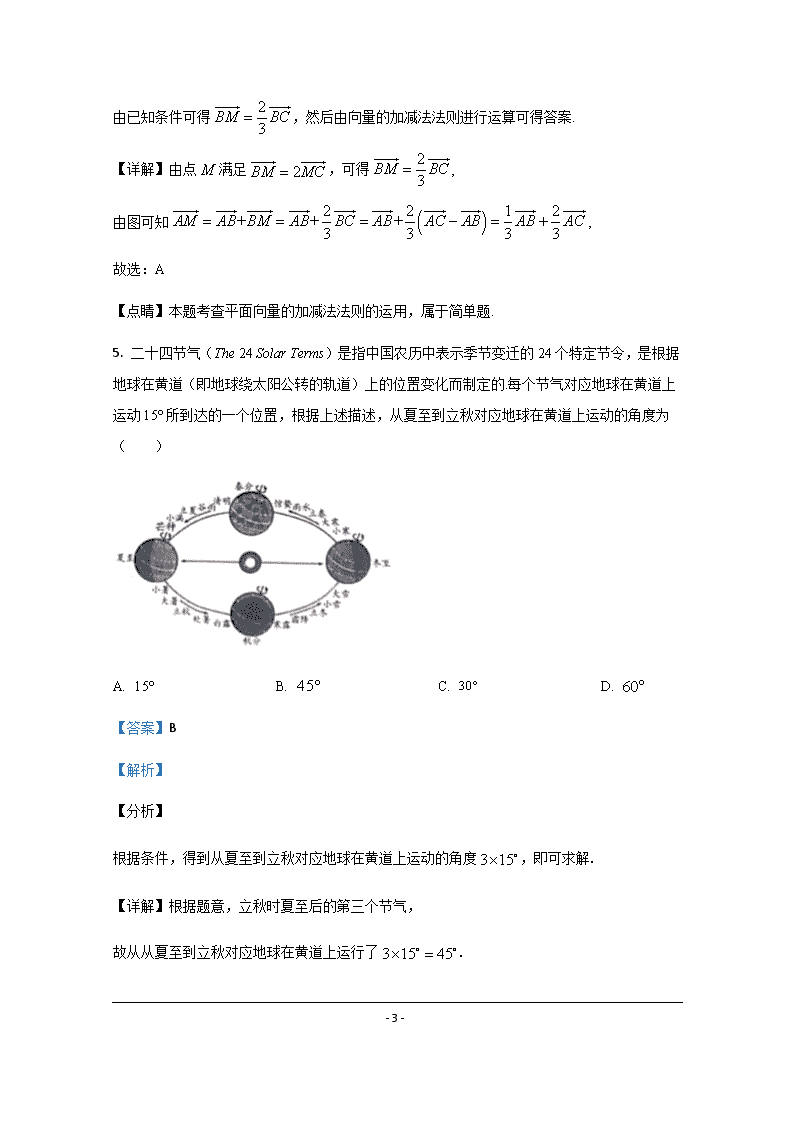‎ ‎【答案】A ‎【解析】‎ ‎【分析】‎ - 26 -‎ 由已知条件可得，然后由向量的加减法法则进行运算可得答案.‎ ‎【详解】由点满足，可得,‎ 由图可知,‎ 故选：A ‎【点睛】本题考查平面向量的加减法法则的运用，属于简单题.‎ ‎5. 二十四节气（The 24 Solar Terms）是指中国农历中表示季节变迁的24个特定节令，是根据地球在黄道（即地球绕太阳公转的轨道）上的位置变化而制定的.每个节气对应地球在黄道上运动所到达的一个位置，根据上述描述，从夏至到立秋对应地球在黄道上运动的角度为（ ）‎ A. B. C. D. ‎ ‎【答案】B ‎【解析】‎ ‎【分析】‎ 根据条件，得到从夏至到立秋对应地球在黄道上运动的角度，即可求解.‎ ‎【详解】根据题意，立秋时夏至后的第三个节气，‎ 故从从夏至到立秋对应地球在黄道上运行了.‎ - 26 -‎ 故选：B.‎ ‎【点睛】本题考查了合情推理的应用，着重考查学生阅读理解能力，以及计算能力，属于基础题.‎ ‎6. 已知，则（ ）‎ A. B. C. D. ‎ ‎【答案】D ‎【解析】‎ ‎【分析】‎ 由，代入即可求解.‎ ‎【详解】因为，‎ 由 故选：D.‎ ‎【点睛】本题主要考查了三角恒等变换的化简、求值，其中解答中熟记余弦的倍角公式，准确运算是解答的关键，着重考查了运算与求解能力.‎ ‎7. 已知一个圆柱侧面积等于其表面积的，且其轴截面的周长为24，则该圆柱的体积为（ ）‎ A. B. C. D. ‎ ‎【答案】D ‎【解析】‎ - 26 -‎ ‎【分析】‎ 设圆柱的底面半径为，高为，则由题意得，，解方程组，再根据圆柱的体积公式求解即可．‎ ‎【详解】设圆柱的底面半径为，高为，‎ ‎∵圆柱侧面积等于表面积的，且其轴截面的周长是24，‎ ‎∴，解得，‎ ‎∴圆柱的体积为，‎ 故选:D．‎ ‎【点睛】本题主要考查圆柱的表面积公式与体积公式，属于基础题．‎ ‎8. 若函数的最小正周期为，则（ ）‎ A. B. ‎ C. D. ‎ ‎【答案】C ‎【解析】‎ ‎【分析】‎ 先求得，求得函数在上单调递增，结合，‎ - 26 -‎ ‎，利用单调性作出比较，即可求解.‎ ‎【详解】由题意，函数的最小正周期为，‎ 可得，解得，即，‎ 令，即，‎ 当时，，即函数在上单调递增，‎ 又由，‎ 又由，所以.‎ 故选：C.‎ ‎【点睛】本题主要考查了正切函数的图象与性质的应用，其中解答中熟记正切函数的图象与性质，合理应用函数的单调性进行比较是解答的关键，着重考查推理与运算能力.‎ 二、多项选择题：本大题共4小题，每小题5分，共20分.在每小题给出的四个选项中，有多项符合题目要求，全部选对的得5分，选对但不全的得3分，有选错的得0分.‎ ‎9. 若，，是任意的非零向量，则下列叙述正确的是（ ）‎ A. 若，则 B. 若，则 C. 若，，则 - 26 -‎ D. 若，则 ‎【答案】ACD ‎【解析】‎ ‎【分析】‎ 根据平面向量的定义、数量积定义、共线向量定义进行判断．‎ ‎【详解】对应，若，则向量长度相等，方向相同，故，故正确；‎ 对于，当且时，，但，可以不相等，故错误；‎ 对应，若，，则方向相同或相反，方向相同或相反，‎ 故的方向相同或相反，故，故正确；‎ 对应，若，则，‎ ‎，，故正确．‎ 故选：‎ ‎【点睛】本题考查平面向量的有关定义，性质，数量积与向量间的关系，属于中档题．‎ ‎10. 下列叙述正确的是（ ）‎ A. 已知，是空间中的两条直线，若，则直线与平行或异面 B. 已知是空间中的一条直线，是空间中的一个平面，若，则或与只有一个公共点 C. 已知，是空间两个不同的平面，若，则，必相交于一条直线 D. 已知直线与平面相交，且垂直于平面内的无数条直线，则 - 26 -‎ ‎【答案】ABC ‎【解析】‎ ‎【分析】‎ 对于A，根据空间直线位置关系的定义即可判断；对于B，根据线面位置关系的定义即可判断；对于B，根据平面与平面的位置关系的定义即可判断；对于D，根据线面垂直的判定定理即可判断 ‎【详解】解：对于A，根据空间中直线的位置关系有：相交、平行、异面，由题意可知，说明直线与不相交，即直线与平行或异面，故A正确；‎ 对于B，根据直线与平面的位置关系有：直线与平面相交、直线与平面平行、直线在平面内，因为，所以直线与平面不平行，即直线与平面相交或直线在平面内，从而得或与只有一个公共点，故B正确；‎ 对于C，因为平面与平面的位置关系有：相交或平面，因为，是空间两个不同的平面，而，所以平面与相交，即，必相交于一条直线，故C正确；‎ 对于D，当直线与平面相交，且垂直于平面内的无数条直线，若这些直线中没有相交直线，则不一定垂直平面，故D 不正确，‎ 故选：ABC ‎【点睛】此题考查空间中直线与直线、直线与平面、平面与平面的位置关系的理解和应用，以及线面垂直的判定定理的理解，属于中档题.‎ ‎11. 在中，，，分别是内角，，所对的边，，且，，则以下说法正确的是（ ）‎ A. ‎ B. 若，则 - 26 -‎ C. 若，则是等边三角形 D. 若的面积是，则该三角形外接圆半径为4‎ ‎【答案】AC ‎【解析】‎ ‎【分析】‎ 对于，利用正弦定理可将条件转化得到，即可求出；‎ 对于，利用正弦定理可求得，进而可得；‎ 对于，利用正弦定理条件可转化为，结合原题干条件可得，进而求得；‎ 对于，根据三角形面积公式求得，利用余弦定理求得，进而由正弦定理求得．‎ ‎【详解】解：由正弦定理可将条件转化为，‎ 因为，故，‎ 因为，则，故正确；‎ 若，则由正弦定理可知，则，‎ 因为，则，故错误；‎ 若，根据正弦定理可得，‎ 又因为，即，即有，所以，‎ 因为，则，故，‎ - 26 -‎ 整理得，即，‎ 解得，故，则，‎ 即，所以是等边三角形，故正确；‎ 若的面积是，即，解得，‎ 由余弦定理可得，即 设三角形的外接圆半径是，‎ 由正弦定理可得，则该三角形外接圆半径为2，故D错误，‎ 故选：AC．‎ ‎【点睛】本题考查正余弦定理的应用及同角三角函数的基本关系和两角和与差的三角公式，转化思想，计算能力，属于中档题．‎ ‎12. 水车在古代是进行灌溉引水的工具，是人类的一项古老的发明，也是人类利用自然和改造自然的象征，如图是一个半径为的水车，一个水斗从点出发，沿圆周按逆时针方向匀速旋转，且旋转一周用时120秒.经过秒后，水斗旋转到点，设点的坐标为，其纵坐标满足，则下列叙述正确的是（ ）‎ - 26 -‎ A. ‎ B. 当时，函数单调递增 C. 当时，点到轴距离的最大值为 D. 当时，‎ ‎【答案】AD ‎【解析】‎ ‎【分析】‎ 求出函数的解析式，再分析选项，即可得出结论.‎ ‎【详解】由题意，R＝＝6，T＝120＝，∴ω＝，当t＝0时，y＝f(t)＝，‎ 代入可得＝6sin φ，∵，∴φ＝－.故A正确；‎ 所以，当时，，所以函数在不是单调递增的，故B不正确；‎ 因为，，所以点P到x轴的距离的最大值为6，故C不正确；‎ 当时，，此时，点，，故D正确，‎ 故选：AD．‎ ‎【点睛】‎ - 26 -‎ 本题考查的是有关函数的应用问题，涉及到的知识点有数学建模，将实际问题转化为函数问题来解决，结合三角函数的相应的性质求得结果，属于中档题.‎ 三、填空题：本题共4小题，每小题5分，共20分.‎ ‎13. 已知复数，的共轭复数为，则________.‎ ‎【答案】1‎ ‎【解析】‎ ‎【分析】‎ 根据共轭复数的概念，先求出复数的共轭复数，再根据复数的乘法运算，即可求出结果.‎ ‎【详解】复数的共轭复数为 所以.‎ 故答案为：1.‎ ‎【点睛】本题考查了共轭复数的概念，以及复数的乘法运算，属于基础题.‎ ‎14. 已知正四棱锥的侧面都是等边三角形，且高为2，则该正四棱锥的斜高为________.‎ ‎【答案】‎ ‎【解析】‎ ‎【分析】‎ 由题意画出草图，设，结合高和等边三角形的性质，利用勾股定理，可求，由此即可求出结果.‎ ‎【详解】如图，四棱锥为正四棱锥，由题意可知，高，取中点，连接，，则为正四棱锥的斜高.‎ - 26 -‎ 设，则，‎ 在等边三角形中，由，得 在中， ，‎ 由勾股定理，可得，解得 ‎ 所以该正四棱锥的斜高为 ‎ 故答案为： .‎ ‎【点睛】本题考查棱锥的结构特征，考査运算求解能力，是基础题.‎ ‎15. 若函数的最小正周期为，将的图像向左平移个单位后，所得图像关于轴对称，则的最小正值为________.‎ ‎【答案】‎ ‎【解析】‎ ‎【分析】‎ 利用函数的图像变换规律，正弦函数的周期性、图像的对称性，求得和的值，即可得解 ‎【详解】解：因为函数的最小正周期为，‎ 所以，‎ - 26 -‎ 所以其图像向左平移个单位后，可得的图像，‎ 因为所得图像关于轴对称，‎ 所以，即，‎ 所以的最小正值为，‎ 故答案为：‎ ‎【点睛】此题考查函数的图像变换规律，正弦函数的周期性、对称性，属于基础题.‎ ‎16. 已知两个非零向量，，，若，则________；若存在两个不同的，使得成立，则正数的取值范围是________.‎ ‎【答案】 (1). (2). ‎ ‎【解析】‎ ‎【分析】‎ 根据数量积的坐标运算公式计算，分离参数可得，根据有两解求出的范围，从而得出的范围．‎ ‎【详解】，‎ ‎，故，．‎ - 26 -‎ 又，，．‎ 由可得：，‎ 令，，，则在，上单调递增，在，上单调递减，‎ 且，，．‎ 存在两个不同的，使得成立，‎ 故存在两个不同的，使得成立，‎ ‎，‎ ‎，‎ ‎．‎ 故答案为：；，‎ ‎【点睛】本题考查了平面向量的数量积运算，考查三角恒等变换，属于中档题．‎ 四、解答题：本题共6小题，共70分，解答应写出文字说明、证明过程或演算步骤.‎ ‎17. 已知角的顶点与坐标原点重合，始边落在轴的正半轴上，终边经过点 - 26 -‎ ‎，其中.‎ ‎（1）若，求的值；‎ ‎（2）若，求的值.‎ ‎【答案】（1）；（2）.‎ ‎【解析】‎ ‎【分析】‎ ‎（1）用三角函数的定义；‎ ‎（2）先求正切值，再把弦化切.‎ ‎【详解】（1）由题意知，，‎ 因为，‎ 所以.‎ 解得，‎ 所以.‎ ‎（2）当时，，‎ 所以.‎ ‎【点睛】本题为基础题，考查三角函数的定义及同角三角函数的关系.‎ ‎18. 某广场设置了一些多面体形或球形的石凳供市民休息.如图（1）的多面体石凳是由图（2‎ - 26 -‎ ‎）的正方体石块截去八个相同的四面体得到，且该石凳的体积是.‎ ‎（1）求正方体石块的棱长；‎ ‎（2）若将图（2）的正方体石块打磨成一个球形的石凳，求此球形石凳的最大表面积.‎ ‎【答案】（1）；（2）.‎ ‎【解析】‎ ‎【分析】‎ ‎（1）设正方体石块的棱长为，求出每个截去的四面体的体积，再由等体积法列式求解值；‎ ‎（2）当球形石凳的面与正方体的各个面都相切时球形石凳的表面积最大，可得正方体的棱长正好是球的直径，再由球的表面积公式求解．‎ ‎【详解】（1）设正方体石块的棱长为，‎ 则每个截去的四面体的体积为．‎ 由题意可得，解得．‎ 故正方体石块的棱长为；‎ ‎（2）当球形石凳的面与正方体的各个面都相切时球形石凳的表面积最大．‎ 此时正方体的棱长正好是球的直径，‎ 球形石凳的表面积．‎ - 26 -‎ ‎【点睛】本题考查多面体体积的求法，考查空间想象能力与运算求解能力，是中档题．‎ ‎19. 已知向量，，.‎ ‎（1）若与向量垂直，求实数的值；‎ ‎（2）若向量，且与向量平行，求实数的值.‎ ‎【答案】（1）；（2）.‎ ‎【解析】‎ ‎【分析】‎ ‎（1）求出，解方程即得解；‎ ‎（2）由已知得，解方程即得解.‎ ‎【详解】（1）由已知得，‎ ‎，‎ 所以，‎ 即，‎ 解得；‎ ‎（2）由已知得，‎ 因为，‎ 所以，‎ 解得.‎ - 26 -‎ ‎【点睛】本题主要考查平面向量的线性运算，考查向量垂直平行的坐标表示，意在考查学生对这些知识的理解掌握水平.‎ ‎20. 从①，②这两个条件中选一个，补充到下面问题中，并完成解答.已知中，，，分别是内角，，所对的边，且.‎ ‎（1）求角；‎ ‎（2）已知，且________，求的值及的面积.（注：如果选择多个条件分别解答，按第一个解答计分）‎ ‎【答案】（1）；（2），.‎ ‎【解析】‎ ‎【分析】‎ ‎（1）由已知条件结合正弦定理可得，再利用余弦定理可求出角；‎ ‎（2）若选①，则可求出角，再利用正弦定理求出的值，然后利用三角形的面积公式求出结果；若选②，则先利用正弦定理求出，从而可求出，再利用正弦定理求出的值，然后利用三角形的面积公式求出结果 ‎【详解】（1）因为，‎ 由正弦定理得，‎ 即，‎ 得，‎ 又，‎ - 26 -‎ 所以；‎ ‎（2）选择①时：，，‎ 故；‎ 根据正弦定理，故，‎ 故.‎ 选择②时：，根据正弦定理，‎ 故，‎ 解得，‎ ‎，‎ 根据正弦定理，故，‎ 故.‎ ‎【点睛】此题考查正弦定理和余弦定理的应用，考查三角形面积公式的应用，考查计算能力，属于中档题.‎ ‎21. ‎ - 26 -‎ 某市获得全国文明城市荣誉后，着力健全完善创建工作长效机制，把文明城市创建不断引向深入.近年来，该市规划建设了一批富有地方特色、彰显独特个性的城市主题公园，某主题公园为五边形区域（如图所示），其中三角形区域为健身休闲区，四边形区域为文娱活动区，，，，，，为主题公园的主要道路（不考虑宽度），已知，，，.‎ ‎（1）求道路的长度；‎ ‎（2）求道路，长度之和的最大值.‎ ‎【答案】（1）；（2）.‎ ‎【解析】‎ ‎【分析】‎ ‎（1）如图，连接，由余弦定理求出，再利用正弦定理求出，即得的长度；‎ ‎（2）设，利用正弦定理求出，再利用三角函数求和的最大值.‎ ‎【详解】（1）如图，连接，中，‎ 由余弦定理得 ‎，‎ 所以，‎ - 26 -‎ 因为，所以，‎ 又，所以，‎ 在中，，，，‎ 由正弦定理得，‎ 所以，或（舍去），‎ 所以，，得，‎ 即的长度是.‎ ‎（2）设，因为，所以，‎ 在中，由正弦定理得，‎ 因为，‎ 所以，，‎ 所以 ‎，‎ - 26 -‎ 因为，所以，‎ 所以当，即时，取得最大值，‎ 即道路，长度之和的最大值为.‎ ‎【点睛】本题主要考查三角函数的应用，考查正弦定理余弦定理解三角形，考查三角函数的图象和性质的应用，意在考查学生对这些知识的理解掌握水平.‎ ‎22. 已知函数的图象如图所示.‎ ‎（1）求函数的单调递增区间；‎ ‎（2）将函数的图象向右平移个单位长度得到曲线，把上各点的横坐标伸长到原来的2倍，纵坐标不变，得到的曲线对应的函数记作.‎ ‎（i）求函数的最大值；‎ ‎（ii）若函数在内恰有2015个零点，求、的值.‎ ‎【答案】（1），；（2）（i）；（ii），.‎ ‎【解析】‎ ‎【分析】‎ - 26 -‎ ‎（1）由函数的图象的顶点坐标求出 ，由周期求出，由五点法作图求出的值，可得函数的解析式，再利用正弦函数的增区间，求得函数的单调递增区间.‎ ‎（2）根据函数的图象变换规律，求得的解析式.‎ ‎（i）从而得到的解析式,再利用正弦函数的定义域和值域求得在的最大值.‎ ‎（ii）令,令，得，易知，方程必有两个不同的实数根、，由，则、异号，再分情况讨论求出求、的值.‎ ‎【详解】（1）由图象可得，‎ 最小正周期，‎ 则，‎ 由，‎ 所以，，‎ 又，则易求得，‎ 所以，‎ 由，，‎ 得，，‎ - 26 -‎ 所以单调递增区间为，.‎ ‎（2）（i）由题意得，‎ ‎，‎ 所以的最大值为；‎ ‎（ii）令，可得，令，‎ 得，易知，方程必有两个不同的实数根、，‎ 由，则、异号，‎ ‎①当且或者且时，则方程和在区间均有偶数个根，不合题意，舍去；‎ ‎②当且0时，则方程和在区间均有偶数个根，不合题意，舍去；‎ ‎③当且，当时，，只有一根，有两根，‎ 所以，关于的方程在上有三个根，‎ 由于，则方程在上有2013‎ - 26 -‎ 个根，由于方程在区间上只有一个根，方程在区间上两个根，因此，不合题意，舍去；‎ ‎④当时，则，当时，只有一根，有两根，‎ 所以，关于的方程在上有三个根，‎ 由于，则方程在上有2013个根，由于方程在区间上有两个根，方程在区间上有一个根，此时，满足题意；‎ 因此，，，‎ 得，‎ 综上，，.‎ ‎【点睛】本题主要考查由函数的部分图象求解析式，由函数的图象的顶点坐标求出 ，由周期求出，由五点法作图求出的值，正弦函数的增区间，函数的图象变换规律，正弦函数的定义域和值域，属于中档题.‎ - 26 -‎