辽宁省沈阳市铁路实验中学2019-2020学年高一上学期10月月考数学试题 16页

www.ks5u.com 沈阳铁路实验中学2019-2020学年度上学期10月月考试题 高一数学 一、单选题 ‎1.已知全集，集合，，则（ ）‎ A. B. ‎ C. D. ‎ ‎【答案】A ‎【解析】‎ ‎【分析】‎ 本题根据交集、补集的定义可得.容易题，注重了基础知识、基本计算能力的考查.‎ ‎【详解】，则 ‎【点睛】易于理解集补集概念、交集概念有误.‎ ‎2.设是奇数集，是偶数集，则命题“，”的否定是 （ )‎ A. ， B. ，‎ C. ， D. ，‎ ‎【答案】A ‎【解析】‎ ‎【分析】‎ 全称命题的否定为特称命题，排除C,D，的否定为.‎ ‎【详解】“，”即“所有，都有”，它的否定应该是“存在，使”，所以正确选项为A.‎ ‎【点睛】本题考查全称命题否定，注意任意要改成存在，考查对命题否定的理解.‎ ‎3.已知集合A满足条件，则集合A的个数为（ ）‎ A. 8 B. 7 C. 4 D. 3‎ ‎【答案】B ‎【解析】‎ ‎【分析】‎ 利用集合间的关系可知：集合A中除了含有1，2两个元素以外，可能含有另外的元素，据此即可求出．‎ ‎【详解】集合A中必须有元素1和2，可有3，4，5这三个元素中的0个，1个，2个，‎ 故集合A的个数有个，‎ 故选：B．‎ ‎【点睛】熟练掌握集合间的包含关系是解题的关键，本题是一道基础题．‎ ‎4.已知实数，则与的大小关系为（ ）‎ A. B. ‎ C. D. ‎ ‎【答案】A ‎【解析】‎ ‎【分析】‎ 利用作差的方式，可将差配凑为，根据可知，从而得到结论.‎ ‎【详解】‎ ‎ ，又 ‎ 即 本题正确选项：‎ ‎【点睛】本题考查利用作差法比较两式的大小，关键是能够将差配凑成能够判断正负的式子的形式.‎ ‎5.对任意的实数，在下列命题中的真命题是（ ）‎ A. “”是“”的必要不充分条件 B. “”是“”的必要不充分条件 C. “”是“”的充分不必要条件 D. 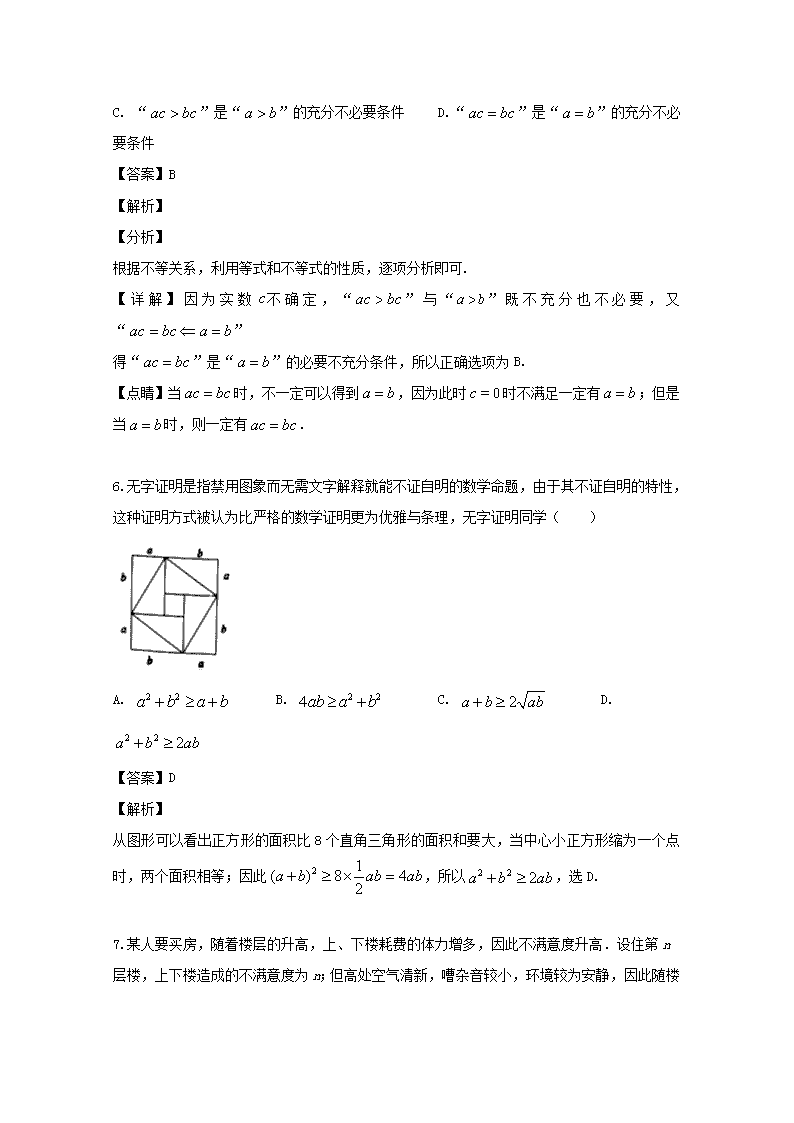“”是“”的充分不必要条件 ‎【答案】B ‎【解析】‎ ‎【分析】‎ 根据不等关系，利用等式和不等式的性质，逐项分析即可.‎ ‎【详解】因为实数不确定，“”与“”既不充分也不必要，又“”‎ 得“”是“”的必要不充分条件，所以正确选项为B.‎ ‎【点睛】当时，不一定可以得到，因为此时时不满足一定有；但是当时，则一定有.‎ ‎6.无字证明是指禁用图象而无需文字解释就能不证自明的数学命题，由于其不证自明的特性，这种证明方式被认为比严格的数学证明更为优雅与条理，无字证明同学（ ）‎ A. B. C. D. ‎ ‎【答案】D ‎【解析】‎ 从图形可以看出正方形的面积比8个直角三角形的面积和要大，当中心小正方形缩为一个点时，两个面积相等；因此，所以，选D.‎ ‎7.某人要买房，随着楼层的升高，上、下楼耗费的体力增多，因此不满意度升高．设住第n层楼，上下楼造成的不满意度为n ‎；但高处空气清新，嘈杂音较小，环境较为安静，因此随楼层升高，环境不满意度降低，设住第n层楼时，环境不满意程度为，则此人应选()‎ A. 1楼 B. 2楼 C. 3楼 D. 4楼 ‎【答案】C ‎【解析】‎ ‎【分析】‎ 根据题意，可知总的不满意度，利用基本不等式求得其最小值，即可得到答案.‎ ‎【详解】由题意，可得总的不满意度为：，当且仅当，即时等号成立，所以选三楼，故选C.‎ ‎【点睛】本题主要考查了基本不等式在最值问题中的应用，其中解答中认真审题，得出总的不满意度的表达式是解答的关键，着重考查了分析问题和解答问题的能力，属于基础题.‎ ‎8.若正实数，满足，则有下列结论：①；②；③；④.其中正确结论的个数为（ ）‎ A. 1 B. 2 C. 3 D. 4‎ ‎【答案】C ‎【解析】‎ ‎【分析】‎ 根据不等式的基本性质，逐项推理判断，即可求解，得到答案.‎ ‎【详解】由题意，正实数是正数，且，‎ ‎①中，可得，所以是错误的；‎ ‎②中，由，可得是正确；‎ ‎③中，根据实数的性质，可得是正确的；‎ ‎④中，因为，所以是正确的，‎ 故选C.‎ ‎【点睛】本题主要考查了不等式的性质的应用，其中解答中熟记不等式的基本性质，合理推理是解答的关键，着重考查了推理与运算能力，属于基础题.‎ ‎9.关于命题“当时，方程没有实数解”，下列说法正确的是 （ )‎ A. 是全称量词命题，假命题 B. 是全称量词命题，真命题 C. 是存在量词命题，假命题 D. 是存在量词命题，真命题 ‎【答案】A ‎【解析】‎ ‎【分析】‎ 对的理解是取遍区间的所有实数，当时方程有解，从而判断原命题为假命题.‎ ‎【详解】原命题的含义是“对于任意，方程都没有实数解”，但当时，方程有实数解，故命题是含有全称量词的假命题，所以正确选项为A.‎ ‎【点睛】判断命题是特称命题还是全称命题，要注意补上省略词，同时注意判断命题为假命题时，只要能举出反例即可.‎ ‎10.若函数在处取最小值，则等于（ ）‎ A. 3 B. C. D. 4‎ ‎【答案】A ‎【解析】‎ ‎【分析】‎ 将函数的解析式配凑为，再利用基本不等式求出该函数的最小值，利用等号成立得出相应的值，可得出的值.‎ ‎【详解】当时，，则 ‎ ，‎ 当且仅当时，即当时，等号成立，因此，，故选：A.‎ ‎【点睛】本题考查基本不等式等号成立的条件，利用基本不等式要对代数式进行配凑，注意“一正、二定、三相等”这三个条件的应用，考查计算能力，属于中等题.‎ ‎11.盐水溶液的浓度公式为，向盐水中再加入克盐，那么盐水将变得更咸，下面哪一个式子可以说明这一事实（ ）‎ A. B. C. D. ‎ ‎【答案】A ‎【解析】‎ ‎【分析】‎ 向盐水溶液中加入克盐，得出加入后的盐水浓度为，根据盐水更咸，说明盐的浓度更大，由此得出不等关系，可得出正确选项.‎ ‎【详解】向盐水溶液中加入克盐，盐水的浓度变为，此时浓度变大，盐水更咸，即，‎ 故选：A.‎ ‎【点睛】本题考查不等关系的确定，解题时要将题中的文字信息转化为数学语言，考查转化思想，属于基础题.‎ ‎12.对一切实数，当时，二次函数的值恒为非负数，则最大值 A. B. C. 2 D. ‎ ‎【答案】A ‎【解析】‎ ‎【分析】‎ 先配方，然后利用基本不等式和放缩法求b﹣2a﹣的最大值．‎ ‎【详解】解：f（x）＝ax2+bx+c＝a（x+）2+，‎ ‎∵二次函数f（x）＝ax2+bx+c的值恒为非负数，‎ ‎∴a＞0且△＝b2﹣4ac≤0，‎ ‎∵a＜b，∴b＞0，c＞0，‎ ‎∴b2≤4ac，即，‎ 又因为4a+c≥（当且仅当4a＝c时，等号成立）‎ ‎∴b﹣2a﹣＝（2b﹣4a﹣c）＝ [2b﹣（4a+c）]‎ ‎≤ [2b﹣]≤[2b﹣2b]=0‎ b﹣2a﹣最大时0，（当且仅当4a＝c时，等号成立）‎ ‎∴2b﹣4a﹣c的最大值的最大值是0，（当且仅当4a＝c时，等号成立）.‎ 故选：A．‎ ‎【点睛】本题考查二次函数的性质，基本不等式和放缩法求最值，属于综合题，有一定难度．‎ 二、填空题 ‎13.已知实数、，满足，则的取值范围是________.‎ ‎【答案】‎ ‎【解析】‎ ‎【分析】‎ 首先确定所处的范围，由不等式的性质可求得结果.‎ ‎【详解】 ，又 ，即 本题正确结果：‎ ‎【点睛】本题考查利用不等式的性质求解范围的问题，属于基础题.‎ ‎14.若关于的不等式对一切实数都成立，则实数的取值范围是_______．‎ ‎【答案】‎ ‎【解析】‎ ‎【分析】‎ 根据一元二次不等式与二次函数的关系，可知只需判别式，利用所得不等式求得结果.‎ ‎【详解】对恒成立 ，解得：‎ 本题正确结果：‎ ‎【点睛】本题考查一元二次不等式恒成立问题的求解，属于基础题.‎ ‎15.关于的不等式的解集为，则 _____________.‎ ‎【答案】-1‎ ‎【解析】‎ ‎【分析】‎ 由不等式的解集可得到方程的两个根，把代入方程可得p，然后通过解不等式确定q，最后可得结果。‎ ‎【详解】由题意，方程有一个根为1，得，则不等式为，其解集为，得，，所以答案为-1.‎ ‎【点睛】本题主要考查一元二次不等式和一元二次方程的关系。‎ ‎16.已知，二次三项式对于一切实数x恒成立，又，使成立，则的最小值为____．‎ ‎【答案】‎ ‎【解析】‎ 分析：对于一切实数恒成立，可得；再由，使成立，可得，所以可得，可化为，平方后换元，利用基本不等式可得结果.‎ 详解：已知，二次三项式对于一切实数恒成立，‎ ‎，且；‎ 再由，使成立，‎ 可得，‎ ‎，，‎ 令，则 ‎（当时，等号成立），所以，的最小值为，‎ 故的最小值为，故答案为.‎ 点睛：本题主要考查一元二次不等式恒成立问题以及利用基本不等式求最值，属于难题.利用基本不等式求最值时，一定要正确理解和掌握“一正，二定，三相等”的内涵：一正是，首先要判断参数是否为正；二定是，其次要看和或积是否为定值（和定积最大，积定和最小）；三相等是，最后一定要验证等号能否成立（主要注意两点，一是相等时参数否在定义域内，二是多次用或时等号能否同时成立）.‎ 三、解答题 ‎17.已知全集为，集合,求：‎ ‎（）．‎ ‎（）．‎ ‎【答案】（1）；（2）或 ‎【解析】‎ 试题分析：（1）解一元二次不等式得，根据交集定义可得；（2）根据、先求出和，再求.‎ 试题解析：（）即，∴，∴，，∴．‎ ‎（）或，或，∴或．‎ ‎18.设集合A＝{x|x2<4}，B＝{x|1<}．‎ ‎(1)求集合A∩B；‎ ‎(2)若不等式2x2＋ax＋b<0的解集为B，求a，b的值．‎ ‎【答案】(1) A∩B＝{x|－2＜x＜1} (2) a＝4，b＝－6‎ ‎【解析】‎ A＝{x|x2<4}＝{x|－20的解集为(-1,3)可得：方程的两根为且 ‎ 由根与系数的关系可得： ‎ ‎（2）若，则， ‎ ‎， ‎ 所以 ‎ 的最小值为（当且仅当时式中等号成立）‎ ‎(3) 当 ，不等式即 即 ‎ ‎①，不等式可化为，‎ 原不等式的解集为 ‎ ‎② ，原不等式可化为 ‎ ‎∴当时，原不等式的解集为 ‎ 当时，原不等式的解集为 ‎ ‎ 当时，原不等式的解集为 ‎【点睛】本题主要考查了二次不等式与二次方程的关系，一元二次不等式的解法及分类讨论思想的应用．‎