山东省昌邑市第一中学人教版高中数学必修二课件：1.2.1平面的基本性质与推论 26页

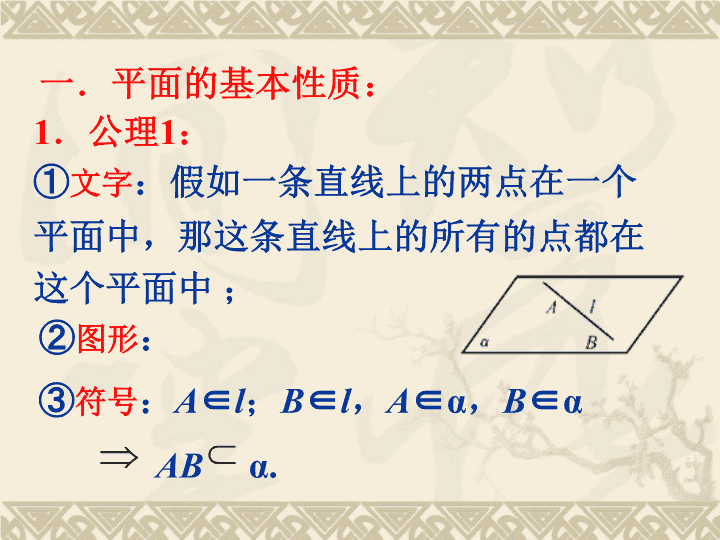
1.2.1 平面的基本性质与推论 一．平面的基本性质： 1 ．公理 1 ： ① 文字 ：假如一条直线上的两点在一个平面中，那这条直线上的所有的点都在这个平面中 ； ② 图形 ： ③ 符号 ： A ∈ l ； B ∈ l ， A ∈α ， B ∈α AB α. 练习 ： （ 1 ） 。 （ 2 ） 。 公理 1 的作用： （ 1 ）作为 判断和证明直线是否在平面内 的依据，即只需要看直线上是否有两个点在平面内就可以了； （ 2 ）公理 1 可以用来 检验某一个面是否为平面 ，检验的具体方法为：把一条直线在面内旋转，固定两个点在面后，如果其他的点也在面内，则该面为平面。 2 ．公理 2 ： ① 文字语言：经过 不在同一条直线 上的三点，有且只有一个平面，也可以说成不共线的三点 确定 一个平面。 ② 图形语言： ③ 符号语言： A 、 B 、 C 三点不共线，有且只有一个平面 α ，使得 A ∈α ， B ∈α ， C ∈α. 如何 理解 公理 2 ？ 公理 2 是 确定平面 的条件 . 深刻理解 “有且只有” 的含义，这里的“有”是说平面存在，“只有”是说平面惟一，“有且只有”强调平面 存在并且惟一 这两方面 . 3. 公理 3 ： ① 文字语言：如果不重合的两个平面有一个公共点，那么它们有且只有一条过这个点的公共直线 . ② 图形语言： ③ 符号语言： P ∈ l . P ∈(α∩β) α∩β= l 如何理解公理 3 ？ (1) 公理 3 反映了 平面与平面的位置关系 ，只要“ 两面共一点 ”，就有“ 两面共一线 ，且过这一点，线惟一” . (2) 从集合的角度看，对于不重合的两个平面，只要他们有公共点，它们就是相交的位置关系， 交集是一条直线 . (3) 公理 3 的作用 : 其一判定 两个平面是否相交 ; 其二可以 判定点在直线上 . 点是某两个平面的公共点，线是这两个平面的公共交线，则这点在线上 . 因此它还是证明 点共线 或 线共点 ，并且作为 画截面 的依据 . 二 . 平面基本性质的推论 文字语言 ：经过一条直线和直线外的一点，有且只有一个平面 . 图形语言： 符号语言： a 与 A 共属于平面 α 且平面 α 惟一 . （ 1 ） 推论 1 ： a 是任意一条直线 点 A a （ 2 ）推论 2 ： 文字语言 : 经过两条相交直线，有且只有一个平面 . 图形语言： 符号语言： a ， b 共面于平面 α ，且 α 是惟一的 . b 是任意一条直线 a 是任意一条直线 a ∩ b = A （ 2 ）推论 3 ： 文字语言 : 经过两条平行直线，有且只有一个平面 . 图形语言： 符号语言： a ， b 共面于平面 α ，且 α 是惟一的 . a ， b 是两条直线 a // b m 图 2 l 三、空间中两直线的位置关系 l m P 图 1 从图中可见，直线 l 与 m 既不相交，也不平行。空间中直线之间的这种关系称为 异面直线 。 不同在任何一个平面内的两条直线叫做 异面直线 。（既不相交也不平行的两条直线 ） 1 、异面直线 判断： (1) 图中直线 m 和 l 是异面直线吗 ? α β l m m l (2) , 则 a 与 b 是异面直线吗？ (3) a , b 不同在平面 α 内 , 则 a 与 b 是异面吗？ 异面直线的画法 : 通常用一个或两个平面来衬托 , 异面直线 不同在任何一个平面 的特点 . (1) 相交 (2) 平行 只有一个公共点 没有公共点 在同一平面 m l 2 、空间中两直线的三种位置关系 (3) 异面直线 m P l 没有公共点 不同在任一平面 m l P 探究 : H G C A D B E F G H E F(B) (C) D A 一个正方体的展开图如上，则 AB , CD , EF , GH 这四条线段所在的直线是异面直线的有几对 ? 相交直线有几对 ? 平行直线有几对 ? 直线和平面位置关系的符号表示 . （ 1 ）点 A 在平面 α 内，记作 A ∈α ，点 B 不在平面 α 内，记作 B α ； （ 2 ）直线 l 在平面 α 内，记作 l α ，直线 m 不在平面 α 内，记作 m α ； （ 3 ）平面 α 与平面 β 相交于直线 l ，记作 α∩β= l ； （ 4 ）直线 l 和 m 相交于点 A ，记作 l ∩ m ={ A }, 简记为 l ∩ m = A . 例 1 ．如图，平面 ABEF 记作 α ，平面 ABCD 记作 β ，根据图形填写： （ 1 ） A ∈α ， B α ， E α ， C α ， D α ； （ 2 ） A ∈β ， B β ， C β ， D β ， E β ， F β ； （ 3 ） α∩β= ； ∈ ∈ ∈ ∈ ∈ AB 例 2 ．如图中 △ ABC ，若 AB 、 BC 在平面 α 内，判断 AC 是否在平面 α 内？ 解： ∵ AB 在平面 α 内， ∴ A 点一定在平面 α 内，又 BC 在平面 α 内， ∴ C 点一定在平面 α 内， ( 点 A 、点 C 都在平面 α 内， ) 直线 AC 在平面 α 内（公理 1 ） . 例 3 ．（ 1 ）不共面的四点可以确定几个平面？ （ 2 ）三条直线两两平行，但不共面，它们可以确定几个平面？ （ 3 ）共点的三条直线可以确定几个平面？ 4 个 3 个 1 个或 3 个 例 4 ．如图，在正方体 ABCD － A 1 B 1 C 1 D 1 中， E 、 F 分别为 CC 1 和 AA 1 上的中点，画出平面 BED 1 F 与平面 ABCD 的交线 . 解：在平面 AA 1 D 1 D 内，延长 D 1 F ， ∵ D 1 F 与 DA 不平行，因此 D 1 F 与 DA 必相交于一点，设为 P ， P P 又 ∵ D 1 F 平面 BED 1 F ， P 在平面 BED 1 F 内 . 则 P ∈ D 1 F ， P ∈ DA ， AD 平面 ABCD ， P ∈ 平面 ABCD ， 又 B 为平面 ABCD 与平面 BED 1 F 的公共点， ∴ 连结 PB ， PB 即为平面 BED 1 F 与平面 ABCD 的交线 . 例 5. 如图所示，已知 △ ABC 的三个顶点都不在平面 α 内，它的三边 AB 、 BC 、 AC 延长线后分别交平面 α 于点 P 、 Q 、 R ， 求证：点 P 、 Q 、 R 在同一条直线上 . 证明：由已知 AB 的延长线交平面 α 于点 P ，根据公理 3 ，平面 ABC 与平面 α 必相交于一条直线，设为 l ， ∵ P ∈ 直线 AB ， P ∈ 面 ABC ，又直线 AB ∩ 面 α= P ， ∴ P ∈ 面 α. ∴ P 是面 ABC 与面 α 的公共点， ∵ 面 ABC ∩ 面 α= l ， ∴ P ∈ l ， 同理， Q ∈ l ， R ∈ l ， ∴ 点 P 、 Q 、 R 在同一条直线 l 上 .