2019-2020学年山西省晋中市平遥县第二中学高一10月月考数学试题 10页

‎2019-2020学年山西省晋中市平遥县第二中学高一10月月考数学试题 ‎(满分150分 考试时间120分)‎ 一、 选择题：在每小题给出的四个选项中，只有一项是符合题目要求的 ‎（本大题共 12 小题，每小题 5 分，共 60 分）‎ ‎1．已知全集U={0，1，2，3，4}，集合A={1，2，3}，B={2，4}，则（CUA）∪B=（　）‎ A．{1，2，4} B．{2，3，4} C．{0，2，4} D．{0，2，3，4}‎ ‎2．下列哪组中的两个函数是相等函数（　　）‎ A． B．‎ C． D．‎ ‎3．函数f（x）=﹣x的图象关于（　　）‎ A．x轴对称 B．y轴对称 C．直线y=x对称 D．坐标原点对称 ‎4．已知集合M={y|y=x2﹣1，x∈R}，N={x|y=}，则M∩N=（　　）‎ A．[﹣1，+∞） B．[﹣1，] C．[，+∞） D．∅‎ ‎5.如图表示某人的体重与年龄的关系，则(　　)‎ ‎ A． 体重随年龄的增长而增加 B． 25岁之后体重不变 ‎ C． 体重增加最快的是15岁至25岁 D． 体重增加最快的是15岁之前 6． 函数的单调减区间是(　　)‎ A． (－∞，1)，(1，＋∞) B． (－∞，1)∪(1，＋∞) ‎ C． {x∈R|x≠1} D．R ‎7．若函数f（x）满足f（3x+2）=9x+8，则f（x）的解析式是（ ）‎ A．f（x）=9x+8 B．f（x）=3x+2‎ C．f（x）=﹣3x﹣4 D．f（x）=3x+2或f（x）=﹣3x﹣4‎ ‎8．设f（x）是R上的任意函数，则下列叙述正确的是（　　）‎ A．f（x）f（﹣x）是奇函数 B．f（x）|f（﹣x）|是奇函数 C．f（x）-f（﹣x）是偶函数 D．f（x）+f（﹣x）是偶函数 ‎9．下列说法中，正确的有（　 ）‎ ‎①函数y=的定义域为{x|x≥1}；‎ ‎②函数y=x2+x+1在（0，+∞）上是增函数；‎ ‎③函数f（x）=x3+1（x∈R），若f（a）=2，则f（﹣a）=﹣2；‎ ‎④已知f（x）是R上的增函数，若a+b＞0，则有f（a）+f（b）＞f（﹣a）+f（﹣b）．‎ A．0个 B．1个 C．2个 D．3个 ‎10．设f（x）=ax2+bx+2是定义在[1+a，2]上的偶函数，则f（x）的值域是（　 ）‎ A．[﹣10，2] B．[﹣12，0] C．[﹣12，2] D．与a，b有关，不能确定 ‎11..若函数f(x)＝是定义在R上的减函数，则a的取值范围为(　 )‎ A． B． C． D．‎ ‎12．已知函数f（x）是定义在R上的偶函数，在（﹣∞，0]上有单调性，且 f（-2）＜f（1），则下列不等式成立的是（　　）‎ A．f（﹣1）＜f（2）＜f（3） B．f（2）＜f（3）＜f（﹣4） ‎ C．f（﹣2）＜f（0）＜f（） D．f（5）＜f（﹣3）＜f（﹣1）‎ 一、 填空题(本大题共4小题，每小题5分，共20分.)‎ 13. 若函数y=（x+1）（x﹣a）为偶函数，则a=　 　 ．‎ ‎14．函数 在区间上的最大值_____________.‎ ‎15．已知f(x)＝若f(a)＝10，则a＝________.‎ ‎16.下列结论中:‎ ‎①对于定义在R上的奇函数,总有；‎ ‎②若，则函数不是奇函数；‎ ‎③对应法则和值域相同的两个函数的定义域也相同；‎ 其中正确的是_______________(把你认为正确的序号全写上).‎ 三：解答题(本大题共6小题，共70分. 解答应写出文字说明，证明过程或演算步骤.) ‎ ‎17.（本小题满分10分）‎ 设A={x∈Z||x|≤6}，B={1，2，3}，C={3，4，5，6}，求：‎ ‎（1）A∩（B∩C）； （2）A∩CA（B∪C）．‎ 18. 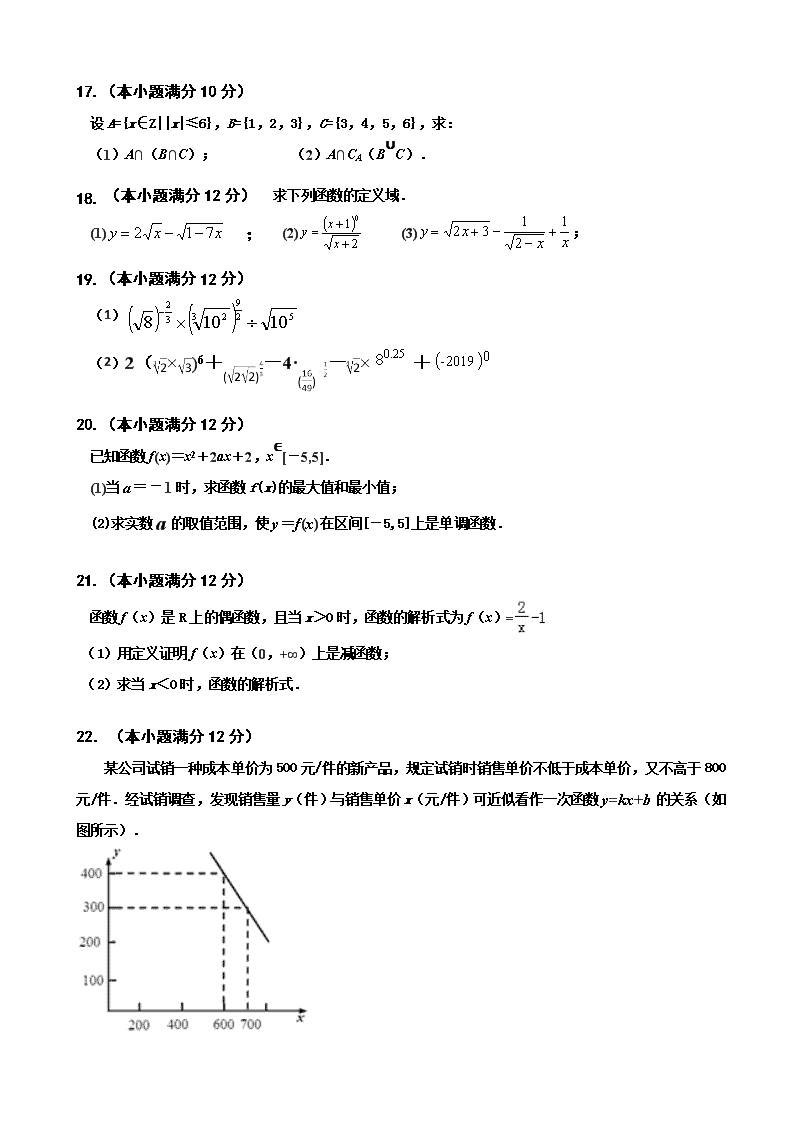‎（本小题满分12分） 求下列函数的定义域．‎ ‎(1) ； (2) (3)；‎ ‎19.（本小题满分12分）‎ ‎（1）‎ ‎（2）2（×)6＋－4·－×＋‎ ‎20.（本小题满分12分）‎ 已知函数f(x)＝x2＋2ax＋2，x∈[－5,5]．‎ ‎(1)当a＝－1时，求函数f(x)的最大值和最小值；‎ ‎(2)求实数a的取值范围，使y＝f(x)在区间[－5,5]上是单调函数．‎ ‎21.（本小题满分12分）‎ 函数f（x）是R上的偶函数，且当x＞0时，函数的解析式为f（x）=‎ ‎（1）用定义证明f（x）在（0，+∞）上是减函数；‎ ‎（2）求当x＜0时，函数的解析式．‎ ‎22．（本小题满分12分）‎ 某公司试销一种成本单价为500元/件的新产品，规定试销时销售单价不低于成本单价，又不高于800元/件．经试销调查，发现销售量y（件）与销售单价x（元/件）可近似看作一次函数y=kx+b的关系（如图所示）．‎ （1） 由图象，求函数y=kx+b的表达式；‎ ‎（2）设公司获得的毛利润（毛利润=销售总价﹣成本总价）为S元．试用销售单价x表示毛利润S，并求销售单价定为多少时，该公司获得最大毛利润？最大毛利润是多少？此时的销售量是多少？‎ ‎ ‎ 班级 姓名 考号 ‎ ‎ -------------------- -------密--------------------- -----------封-------------------------------------线---------------------------------------‎ 平遥二中高一年级十月考试数学答题卡 一、选择题(每题5分，共60分)‎ ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ ‎7‎ ‎8‎ ‎9‎ ‎10‎ ‎11‎ ‎12‎ ‎ ‎ ‎ 二、填空题（每题5分，共20分）‎ ‎13 14 ‎ ‎15 16 ‎ 三.解答题（共70分）‎ ‎17.(本小题满分10分）‎ ‎ ‎ ‎18.(本小题满分12分）‎ ‎19.(本小题满分12分）‎ ‎20.(本小题满分12分）‎ ‎21. (本小题满分12分）‎ ‎22.(本小题满分12分）‎ ‎[.Com]‎ 平遥二中高一年级十月考试数学答案 一、 选择题 ‎ CDDBDA BDCAAD 二、 填空题 ‎13. 1 14. 3 15. －3或5 16.① ‎ 三、 解答题 ‎17.解：∵A={﹣6，﹣5，﹣4，﹣3，﹣2，﹣1，0，1，2，3，4，5，6}‎ ‎（1）又∵B∩C={3}，∴A∩（B∩C）={3}；‎ ‎（2）又∵B∪C={1，2，3，4，5，6}‎ 得CA（B∪C）={﹣6，﹣5，﹣4，﹣3，﹣2，﹣1，0}．‎ ‎∴A∩CA（B∪C）={﹣6，﹣5，﹣4，﹣3，﹣2，﹣1，0}　‎ ‎ 18. 解： ‎ ‎ (1)由得0≤x≤，所以函数y＝2－的定义域为.‎ ‎(2 )由于0的零次幂无意义，故x＋1≠0，即x≠－1.‎ 又x＋2>0，即x>－2，所以x>－2且x≠－1.‎ 所以函数y＝的定义域为.‎ ‎(3)要使函数有意义，需解得－≤x＜2，且x≠0，‎ 所以函数y＝－＋的定义域为.‎ ‎19.（1）原式=×÷＝2－1×103×＝2－1×＝.‎ ‎（2）原式＝2(×)6＋－4×－×＋1＝2×22×33＋2－7－2＋1＝210.‎ ‎20、解：(1)当a＝－1时，f (x)＝x2－2x＋2＝(x－1)2＋1.‎ ‎∵x∈[－5,5]，故当x＝1时，f(x)取得最小值为1，‎ 当x＝－5时，f(x)取得最大值为37.‎ ‎(2)函数f(x)＝(x＋a)2＋2－a2图象的对称轴为x＝－a.‎ ‎∵f(x)在[－5,5]上是单调的，故－a≤－5或－a≥5.即实数a的取值范围是a≤－5或a≥5.‎ ‎21.（1）证明：设a＞b＞0，f（a）﹣f（b）=（﹣1）﹣（﹣1）=，‎ 由a＞b＞0知，＜0，∴f（a）＜f（b），∴f（x）在（0，+∞）上是减函数．‎ ‎（2）解：设x＜0，则﹣x＞0，∴f（﹣x）=﹣1=f（x），‎ ‎∴f（x）=﹣1，即当x＜0时，函数的解析式为 f（x）=﹣1．‎ ‎22.‎ 解：（1）把点（700，300）和点（600，400）分别代入一次函数y=kx+b 可得 300=700k+b，且400=600k+b，解得 k=﹣1，b=1000，‎ 故一次函数y=kx+b的表达式为 y=﹣x+1000（500≤x≤800）．‎ ‎（2）∵公司获得的毛利润（毛利润=销售总价﹣成本总价）为S，‎ 则S=y•x﹣500y=（﹣x+1000 ）x﹣500（﹣x+1000）=﹣x2+1500x﹣500000．‎ 故函数S的对称轴为x=750，满足500≤x≤800，故当x=750时，函数S取得最大值为62500元，‎ 即当销售单价定为750元/价时，该公司可获得最大的毛利润为62500元，此时y=250。‎