2020高中数学 第一章导数的几何意义 8页

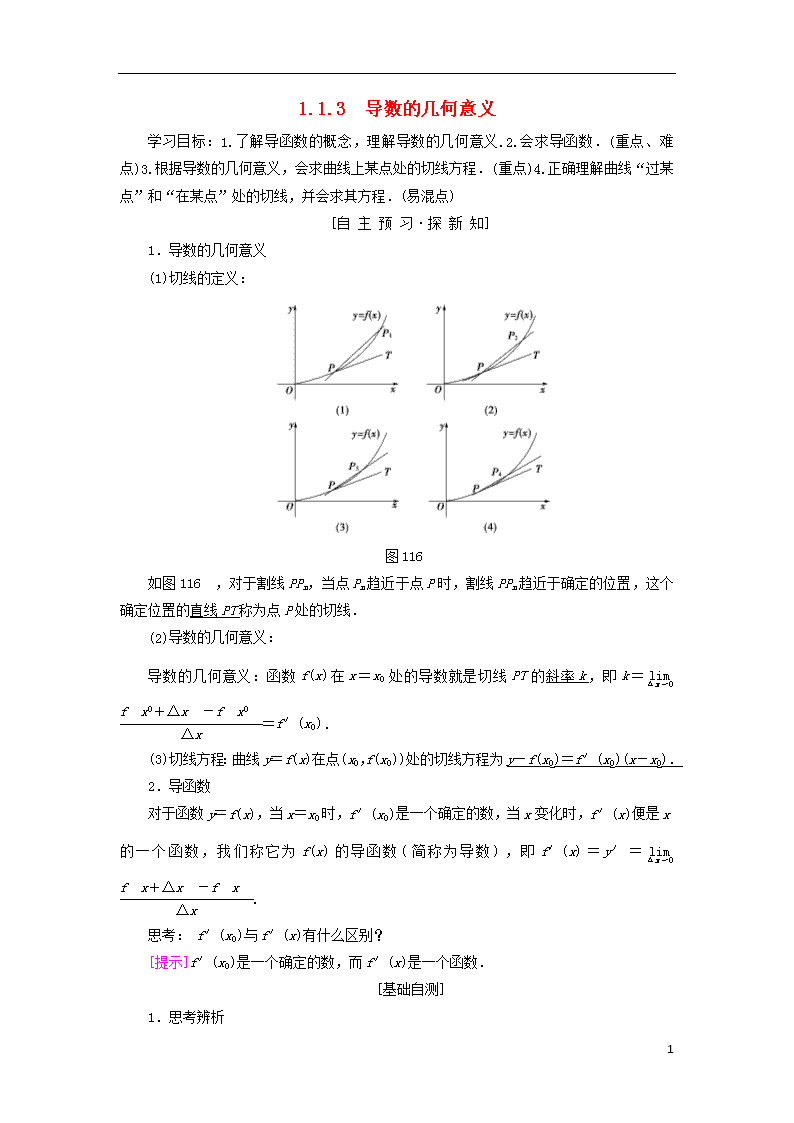
‎1.1.3　‎导数的几何意义 学习目标：1.了解导函数的概念，理解导数的几何意义.2.会求导函数．(重点、难点)3.根据导数的几何意义，会求曲线上某点处的切线方程．(重点)4.正确理解曲线“过某点”和“在某点”处的切线，并会求其方程．(易混点)‎ ‎[自 主 预 习·探 新 知]‎ ‎1．导数的几何意义 ‎(1)切线的定义：‎ 图116‎ 如图116，对于割线PPn，当点Pn趋近于点P时，割线PPn趋近于确定的位置，这个确定位置的直线PT称为点P处的切线．‎ ‎(2)导数的几何意义：‎ 导数的几何意义：函数f(x)在x＝x0处的导数就是切线PT的斜率k，即k＝ ＝f′(x0)．‎ ‎(3)切线方程：曲线y＝f(x)在点(x0，f(x0))处的切线方程为y－f(x0)＝f′(x0)(x－x0)．‎ ‎2．导函数 对于函数y＝f(x)，当x＝x0时，f′(x0)是一个确定的数，当x变化时，f′(x)便是x的一个函数，我们称它为f(x)的导函数(简称为导数)，即f′(x)＝y′＝ .‎ 思考： f′(x0)与f′(x)有什么区别？‎ ‎[提示]f′(x0)是一个确定的数，而f′(x)是一个函数．‎ ‎[基础自测]‎ ‎1．思考辨析 8‎ ‎(1)函数y＝f(x)在x＝x0处的导数f′(x0)的几何意义是曲线y＝f(x)在点x＝x0处切线的斜率．(　　)‎ ‎(2)若曲线y＝f(x)在点(x0，f(x0))处有切线，则f′(x0)必存在．(　　)‎ ‎(3)f′(x0)(或y′|x＝x0)是函数f′(x)在点x＝x0处的函数值．(　　)‎ ‎(4)直线与曲线相切，则直线与已知曲线只有一个公共点．(　　)‎ ‎[答案]　(1)√　(2)×　(3)√　(4)×‎ ‎2．若曲线y＝f(x)在点(x0，f(x0))处的切线方程为2x＋y＋1＝0，则(　　)‎ A．f′(x0)＞0　　　 B．f′(x0)＝0‎ C．f′(x0)＜0 D．f′(x0)不存在 C　[由题意可知，f′(x0)＝－2＜0，故选C.]‎ ‎3．已知函数f(x)在x0处的导数为f′(x0)＝1，则函数f(x)在x0处切线的倾斜角为________. ‎ ‎【导学号：31062012】‎ ‎[解析]　设切线的倾斜角为α，则 tan α＝f′(x0) ＝1，又α∈[0°，180°)，‎ ‎∴α＝45°.‎ ‎[答案]　45°‎ ‎4．若函数f(x)在点A(1,2)处的导数是－1，那么过点A的切线方程是________．‎ ‎[解析]　切线的斜率为k＝－1.‎ ‎∴点 A(1,2)处的切线方程为y－2＝－(x－1)，‎ 即x＋y－3＝0.‎ ‎[答案]　x＋y－3＝0‎ ‎[合 作 探 究·攻 重 难]‎ 导数几何意义的应用 ‎　(1)已知y＝f(x)的图象如图117所示，则f′(xA)与f′(xB)的大小关系是(　　)‎ 图117‎ A．f′(xA)＞f′(xB)‎ 8‎ B．f′(xA)＜f′(xB)‎ C．f′(xA)＝f′(xB)‎ D．不能确定 ‎(2)若曲线y＝x2＋ax＋b在点(0，b)处的切线方程是x－y＋1＝0，则(　　)‎ A．a＝1，b＝1　 B．a＝－1，b＝1‎ C．a＝1，b＝－1 D．a＝－1，b＝－1‎ ‎(1)B　(2)A　[(1)由导数的几何意义，f′(xA)，f′(xB)分别是切线在点A、B处切线的斜率，由图象可知f′(xA)＜f′(xB)．‎ ‎(2)由题意，知k＝y′|x＝0‎ ‎＝ ＝1，∴a＝1.‎ 又(0，b)在切线上，∴b＝1，故选A.]‎ ‎[规律方法]　1.本例(2)中主要涉及了两点：①f′(0)＝1，②f(0)＝b. ‎2.解答此类问题的关键是理解导数的几何意义. ‎3.与导数的几何意义相关的题目往往涉及解析几何的相关知识，如直线的方程、直线间的位置关系等，因此要综合应用所学知识解题.‎ ‎[跟踪训练]‎ ‎1．设曲线y＝ax2在点(1，a)处的切线与直线2x－y－6＝0平行，则a等于 ‎(　　) 【导学号：31062013】‎ A．1 B． C．－ D．－1‎ A　[由题意可知，f′(1)＝2.‎ 又 ＝ ＝ (aΔx＋‎2a)＝‎2a.故由‎2a＝2得a＝1.]‎ ‎2．如图118，函数y＝f(x)的图象在点P(2，y)处的切线是l，则f(2)＋f′(2)等于(　　)‎ 图118‎ A．－4‎ 8‎ B．3‎ C．－2‎ D．1‎ D　[直线l的方程为＋＝1，即x＋y－4＝0.‎ 又由题意可知f(2)＝2，f′(2)＝－1，‎ ‎∴f(2)＋f′(2)＝2－1＝1.]‎ 求切点坐标 ‎　过曲线y＝x2上某点P的切线满足下列条件，分别求出P点．‎ ‎(1) 平行于直线y＝4x－5；‎ ‎(2)垂直于直线2x－6y＋5＝0；‎ ‎(3)与x轴成135°的倾斜角．‎ ‎[解]　f′(x)＝ ＝ ＝2x，设P(x0，y0)是满足条件的点．‎ ‎(1)∵切线与直线y＝4x－5平行，‎ ‎∴2x0＝4，x0＝2，y0＝4，即P(2,4)是满足条件的点．‎ ‎(2)∵切线与直线2x－6y＋5＝0垂直，‎ ‎∴2x0·＝－1，得x0＝－，y0＝，‎ 即P是满足条件的点．‎ ‎(3)∵切线与x轴成135°的倾斜角，‎ ‎∴其斜率为－1.即2x0＝－1，得x0＝－，y0＝，‎ 即P是满足条件的点．‎ ‎[规律方法]　1.本题关键是由条件得到直线的斜率，从而得知函数在某点处的导数，进而求出切点的横坐标. ‎2.根据切线斜率求切点坐标的步骤 (1)设切点坐标(x0，y0)； (2)求导函数f′(x)； (3)求切线的斜率f′(x0)； (4)由斜率间的关系列出关于x0的方程，解方程求x0； (5)x0代入f(x)求y0得切点坐标.‎ ‎ [跟踪训练]‎ 8‎ ‎3．已知曲线y＝2x2－7在点P处的切线方程为8x－y－15＝0，求切点P的坐标. 【导学号：31062014】‎ ‎[解]　设切点P(m，n)，切线斜率为k，‎ 由y′＝ ＝ ‎＝ (4x＋2Δx)＝4x，‎ 得k＝y′|x＝m＝‎4m.‎ 由题意可知‎4m＝8，∴m＝2.‎ 代入y＝2x2－7得n＝1.‎ 故所求切点P为(2,1)．‎ 求曲线的切线方程 ‎[探究问题]‎ ‎1．如何求曲线f(x)在点(x0，f(x0))处的切线方程？‎ 提示：y－y0＝k(x－x0)．即根据导数的几何意义，求出函数y＝f(x)在点(x0，f(x0))处的导数，即曲线在该点处的切线的斜率，再由直线方程的点斜式求出切线方程．‎ ‎2．曲线f(x)在点(x0，f(x0))处的切线与曲线过点(x0，y0)的切线有什么不同？‎ 提示：曲线f(x)在点(x0，f(x0))处的切线，点(x0，f(x0))一定是切点，只要求出k＝f′(x0)，利用点斜式写出切线方程即可；而曲线f(x)过某点(x0，y0)的切线，给出的点(x0，y0)不一定在曲线上，即使在曲线上也不一定是切点．‎ ‎3．曲线在某点处的切线是否与曲线只有一个交点？‎ 提示：不一定．曲线y＝f(x)在点P(x0，y0)处的切线l与曲线y＝f(x)的交点个数不一定只有一个，如图所示．‎ ‎　已知曲线C：y＝x3.‎ ‎(1)求曲线C在横坐标为x＝1的点处的切线方程；‎ ‎(2)求曲线C过点(1,1)的切线方程．‎ ‎[思路探究]　(1)―→―→‎ ‎(2)―→―→‎ ―→ ‎[解]　(1)将x＝1代入曲线C的方程得y＝1，∴切点P(1,1)．‎ y′|x＝1＝ ＝ 8‎ ‎＝[3＋3Δx＋Δx2]＝3.‎ ‎∴k＝y′|x＝1＝3.‎ ‎∴曲线在点P(1,1)处的切线方程为y－1＝3(x－1)，即3x－y－2＝0.‎ ‎(2)设切点为Q(x0，y0)，由(1)可知y′|x＝x0＝3x，由题意可知kPQ＝y′|x＝x0，‎ 即＝3x，又y0＝x，所以＝3x，即2x－x0－1＝0，解得x0＝1或x0＝－.‎ ‎①当x0＝1时，切点坐标为(1,1)，相应的切线方程为3x－y－2＝0.‎ ‎②当x0＝－时，切点坐标为，相应的切线方程为y＋＝，即3x－4y＋1＝0.‎ 母题探究：1.(变结论)第(1)小题中的切线与曲线C是否还有其他的公共点？‎ ‎[解]　由 解得或 从而求得公共点为P(1,1)或M(－2，－8)，‎ 即切线与曲线C的公共点除了切点外，还有另一公共点(－2，－8)．‎ ‎2．(变条件)求曲线y＝f(x)＝x2＋1过点P(1,0)的切线方程．‎ ‎[解]　设切点为Q(a，a2＋1)，＝＝‎2a＋Δx，当Δx趋于0时，(‎2a＋Δx)趋于‎2a，所以所求切线的斜率为‎2a.因此，＝‎2a，解得a＝1±，所求的切线方程为y＝(2＋2)x－(2＋2)或y＝(2－2)x－(2－2)．‎ ‎[规律方法]　利用导数的几何意义求切线方程的方法 (1)若已知点(x0，y0)在已知曲线上，求在点(x0，y0)处的切线方程，先求出函数y＝f(x)在点x0处的导数，然后根据直线的点斜式方程，得切线方程y－y0＝f′(x0)(x－x0). (2)若点(x0，y0)不在曲线上，求过点(x0，y0)的切线方程，首先应设出切点坐标，然后根据导数的几何意义列出等式，求出切点坐标，进而求出切线方程.‎ ‎ [当 堂 达 标·固 双 基]‎ ‎1．已知曲线y＝f(x)在点(1，f(1))处的切线方程为2x－y＋2＝0，则f′(1)＝‎ ‎(　　)‎ A．4　　　 B．－‎4　‎　　‎ C．－2　　　 D．2‎ D　[由导数的几何意义知f′(1)＝2，故选D.]‎ ‎2．下面说法正确的是(　　)‎ 8‎ A．若f′(x0)不存在，则曲线y＝f(x)在点(x0，f(x0))处没有切线 B．若曲线y＝f(x)在点(x0，f(x0))处有切线，则f′(x0)必存在 C．若f′(x0)不存在，则曲线y＝f(x)在点(x0，f(x0))处的切线斜率不存在 D．若曲线y＝f(x)在点(x0，f(x0))处没有切线，则f′(x0)有可能存在 C　[根据导数的几何意义及切线的定义知曲线在(x0，y0)处有导数，则切线一定存在，但反之不一定成立，故A，B，D错误．]‎ ‎3．已知二次函数y＝f(x)的图象如图119所示，则y＝f(x)在A，B两点处的导数f′(a)与f′(b)的大小关系为：‎ f′(a)________f′(b)(填“＜”或“＞”)．‎ 图119‎ ‎[解析]　f′(a)与f′(b)分别表示函数图象在点A，B处的切线斜率，‎ 由图象可得f′(a)＞f′(b)．‎ ‎[答案]　＞‎ ‎4．曲线f(x)＝在点(－2，－1)处的切线方程为________. ‎ ‎【导学号：31062015】‎ ‎[解析]　f′(－2)＝ ‎＝ ＝ ＝－，‎ ‎∴切线方程为y＋1＝－(x＋2)，‎ 即x＋2y＋4＝0.‎ ‎[答案]　x＋2y＋4＝0‎ ‎5．已知直线y＝4x＋a和曲线y＝x3－2x2＋3相切，求切点坐标及a的值．‎ ‎[解]　设直线l与曲线相切于点P(x0，y0)，则 f′(x)＝ ‎＝3x2－4x.‎ 由导数的几何意义，得k＝f′(x0)＝3x－4x0＝4，‎ 8‎ 解得x0＝－或x0＝2，‎ ‎∴切点坐标为或(2,3)．‎ 当切点为时，‎ 有＝4×＋a，‎ ‎∴a＝.‎ 当切点为(2,3)时，有3＝4×2＋a，‎ ‎∴a＝－5，‎ 因此切点坐标为或(2,3)，‎ a的值为或－5.‎ 8‎