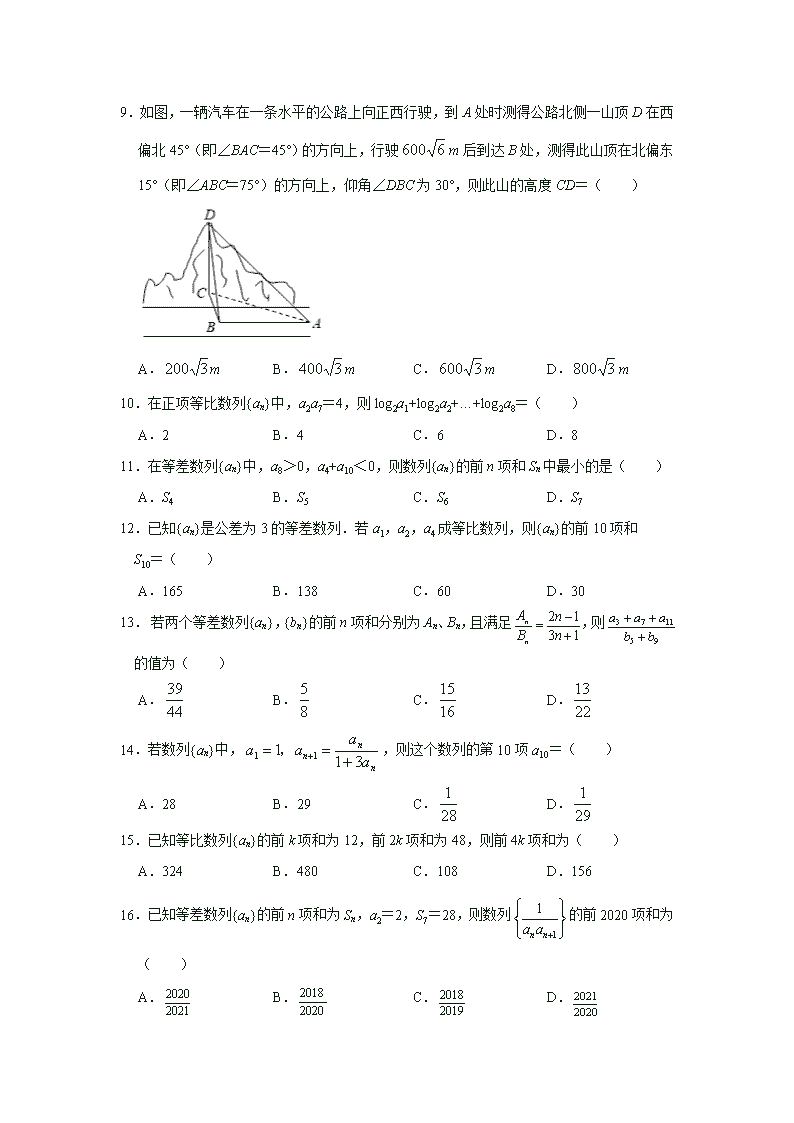【数学】河北省元氏县第一中学2019-2020学年高一下学期期中考试试题（解析版） 15页

河北省元氏县第一中学2019-2020学年 高一下学期期中考试试题 考试时间：120分钟；分值：150分 一．选择题（共24小题，每小题5分，共120分）‎ ‎1．如果a＜b＜0，那么下列不等式中正确的是（　　）‎ A．b2＞ab B．ab＞a2 C．a2＞b2 D．|a|＜|b|‎ ‎2．不等式﹣x2+3x﹣2＞0的解集是（　　）‎ A． B． C． D．‎ ‎3．数列是其第（　　）项 A．17 B．18 C．19 D．20‎ ‎4．在△ABC中，若a＝6，A＝60°，B＝75°，则c＝（　　）‎ A．4 B． C． D．‎ ‎5．在△ABC中，角A，B，C的对边分别为a，b，c，其面积S＝（a2+c2﹣b2），则tanB的值为（　　）‎ A． B．1 C． D．2‎ ‎6．在△ABC中，a，b，c分别为角A、B、C的对边，已知∠A＝60°，b＝1，面积，则等于（　　）‎ A． B． C． D．‎ ‎7．在△ABC中，a＝80，b＝100，A＝30°，则三角形的解的个数是（　　）‎ A．0个 B．1个 C．2个 D．不确定 ‎8．在△ABC中，角A，B，C的对边分别为a，b，c，若c＝b（cosA+cosB），则△ABC为（　　）‎ A．等腰直角三角形 B．直角三角形 ‎ C．等腰三角形 D．等腰三角形或直角三角形 ‎9．如图，一辆汽车在一条水平的公路上向正西行驶，到A处时测得公路北侧一山顶D在西偏北45°（即∠BAC＝45°）的方向上，行驶m后到达B处，测得此山顶在北偏东15°（即∠ABC＝75°）的方向上，仰角∠DBC为30°，则此山的高度CD＝（　　）‎ A．m B．m C．m D．m ‎10．在正项等比数列{an}中，a2a7＝4，则log2a1+log2a2+…+log2a8＝（　　）‎ A．2 B．4 C．6 D．8‎ ‎11．在等差数列{an}中，a8＞0，a4+a10＜0，则数列{an}的前n项和Sn中最小的是（　　）‎ A．S4 B．S5 C．S6 D．S7‎ ‎12．已知{an}是公差为3的等差数列．若a1，a2，a4成等比数列，则{an}的前10项和 S10＝（　　）‎ A．165 B．138 C．60 D．30‎ ‎13． 若两个等差数列{an}，{bn}的前n项和分别为An、Bn，且满足，则的值为（　　）‎ A． B． C． D．‎ ‎14．若数列{an}中，，则这个数列的第10项a10＝（　　）‎ A．28 B．29 C． D．‎ ‎15．已知等比数列{an}的前k项和为12，前2k项和为48，则前4k项和为（　　）‎ A．324 B．480 C．108 D．156‎ ‎16．已知等差数列{an}的前n项和为Sn，a2＝2，S7＝28，则数列的前2020项和为（　　）‎ A． B． C． D．‎ ‎17．数列{an}前n项和为Sn，若2Sn＝an+1，则a7+S2019的值为（　　）‎ A．2 B．1 C．0 D．﹣1‎ ‎18．已知数列{an}的通项，若{an}为单调递增数列，则λ的取值范围是（　　）‎ A．(﹣3，+∞） B．[﹣3，+∞） C．（﹣2，+∞） D．[﹣2，+∞）‎ ‎19．对于任意实数x，不等式ax2+2ax﹣（a+2）＜0恒成立，则实数a的取值范围是（　　）‎ A．﹣1≤a≤0 B．﹣1≤a＜0 C．﹣1＜a≤0 D．﹣1＜a＜0‎ ‎20．若关于x的不等式的解集中恰有4个正整数，则实数m的取值范围为（　　）‎ A．（6，7] B．（6，7） C．[6，7） D．（6，+∞）‎ ‎21．函数的最小值是（　　）‎ A．2 B．4 C．6 D．8‎ ‎22．两个正实数a，b满足3a+b＝1，则满足恒成立的m取值范围（　　）‎ A．[﹣4，3] B．[﹣3，4] C．[﹣2，6] D．[﹣6，2]‎ ‎23．在△ABC中，角A，B，C所对的边分别为a，b，c满足b2+c2﹣a2＝bc，a＝，则b+c的取值范围是（　　）‎ A． B． C． D．‎ ‎24．已知数列{an}的前n项和，设，Tn为数列{bn}的前n项和，若对任意的n∈N*，不等式λTn＜9n+3恒成立，则实数λ的取值范围为（　　）‎ A．（﹣∞，48） B．（﹣∞，36） C．（﹣∞，16） D．（16，+∞）‎ 二．解答题（共3小题，每题10分，共30分）‎ ‎25．已知在△ABC中，角A、B、C对应的边分别为a、b、c，bsinB+asinC＝asinA+csinC．‎ ‎（1）求角B；‎ ‎（2）若c＝1，△ABC的面积为，求C．‎ ‎26．设函数f（x）＝x2+mx+n，已知不等式f（x）＜0的解集为{x|1＜x＜4}．‎ ‎（1）求m和n的值；‎ ‎（2）若对任意x＞0恒成立，求a的取值范围．‎ ‎27．已知等差数列{an}的前n项和为Sn，且满足a4+a6＝18，S11＝121．‎ ‎（1）求数列{an}的通项公式；‎ ‎（2）设bn＝（an+3）2n，数列{bn}的前n项和为Tn，求Tn．‎ 参考答案 一．选择题（共24小题，每小题5分，共120分）‎ ‎1．如果a＜b＜0，那么下列不等式中正确的是（　　）‎ A．b2＞ab B．ab＞a2 C．a2＞b2 D．|a|＜|b|‎ ‎【分析】由a＜b＜0即可得出b2＜ab，ab＜a2，﹣a＞﹣b＞0，进而得出a2＞b2，|a|＞|b|，即得出选项C正确．‎ ‎【解答】解：∵a＜b＜0；∴b2＜ab，ab＜a2，﹣a＞﹣b＞0；∴a2＞b2，|a|＞|b|；∴C正确．‎ 故选：C．‎ ‎2．不等式﹣x2+3x﹣2＞0的解集是（　　）‎ A． B． C． D．‎ ‎【分析】直接求解即可．‎ ‎【解答】解：不等式﹣x2+3x﹣2＞0，即为x2﹣3x+2＜0，‎ 即（x﹣1）（x﹣2）＜0，解得1＜x＜2．‎ 故选：C．‎ ‎3．数列是其第（　　）项 A．17 B．18 C．19 D．20‎ ‎【分析】根据题意，分析归纳可得该数列可以写成，，，……，，可得该数列的通项公式，分析可得答案．‎ ‎【解答】解：根据题意，数列，‎ 可写成，，，……，，‎ 对于7，即＝，为该数列的第20项；‎ 故选：D．‎ ‎4．在△ABC中，若a＝6，A＝60°，B＝75°，则c＝（　　）‎ A．4 B． C． D．‎ ‎【分析】根据三角形内角和求出角C，再根据正弦定理即可求出边c．‎ ‎【解答】解：因为C＝180°﹣75°﹣60°＝45°，‎ 所以根据正弦定理知，，即，解得．‎ 故选：D．‎ ‎5．在△ABC中，角A，B，C的对边分别为a，b，c，其面积S＝（a2+c2﹣b2），则tanB的值为（　　）‎ A． B．1 C． D．2‎ ‎【分析】结合三角形的面积公式以及余弦定理建立方程进行求解即可．‎ ‎【解答】解：∵S＝acsinB，cosB＝，∴a2+c2﹣b2＝2accosB，‎ 由S＝（a2+c2﹣b2），得acsinB＝×2accosB，得tanB＝，‎ 故选：A．‎ ‎6．在△ABC中，a，b，c分别为角A、B、C的对边，已知∠A＝60°，b＝1，面积，则等于（　　）‎ A． B． C． D．‎ ‎【分析】由三角形的面积S＝＝bcsinA，A＝60°，b＝1，可得c＝4，由余弦定理：‎ a2＝b2+c2﹣2bccosA．求解a，利用正弦定理化简即可求解．‎ ‎【解答】解：∵A＝60°，b＝1，‎ 三角形的面积S＝＝bcsinA＝，∴c＝4．‎ ‎∴由余弦定理：a2＝b2+c2﹣2bccosA，即a2＝1+16﹣4，可得：a＝．‎ ‎∴正弦定理可知：＝＝2R ‎＝＝＝．‎ 故选：A．‎ ‎7．在△ABC中，a＝80，b＝100，A＝30°，则三角形的解的个数是（　　）‎ A．0个 B．1个 C．2个 D．不确定 ‎【分析】由正弦定理 解得 sinB＝，故B可能是个锐角，也可能是钝角，故三角形的解的个数是2．‎ ‎【解答】解：由正弦定理可得 ，即 160＝，‎ ‎∴sinB＝，故B可能是个锐角，也可能是钝角，‎ 故三角形的解的个数是2，‎ 故选：C．‎ ‎8．在△ABC中，角A，B，C的对边分别为a，b，c，若c＝b（cosA+cosB），则△ABC为（　　）‎ A．等腰直角三角形 B．直角三角形 ‎ C．等腰三角形 D．等腰三角形或直角三角形 ‎【分析】首先利用正弦定理将等式统一到三角形内角的三角函数等式，然后利用三角函数的变形得到cosB＝0或者sinA＝sinB，从而判断三角形的形状．‎ ‎【解答】解：△ABC中，角A，B，C的对边分别为a，b，c，‎ 若c＝b（cosA+cosB），由正弦定理得到sinC＝sinB（cosA+cosB），‎ 由A+B+C＝π，所以sin（A+B）＝sinB（cosA+cosB），‎ 所以sinAcosB+cosAsinB＝sinBcosA+sinBcosB，整理得到sinAcosB＝sinBcosB，‎ 所以cosB（sinA﹣sinB）＝0，所以cosB＝0或者sinA＝sinB，‎ 所以B＝90°或者A＝B；‎ 故△ABC为直角三角形或者为等腰三角形；‎ 故选：D．‎ ‎9．如图，一辆汽车在一条水平的公路上向正西行驶，到A处时测得公路北侧一山顶D在西偏北45°（即∠BAC＝45°）的方向上，行驶m后到达B处，测得此山顶在北偏东15°（即∠ABC＝75°）的方向上，仰角∠DBC为30°，则此山的高度CD＝（　　）‎ A．m B．m C．m D．m ‎【分析】△ABC中由正弦定理求得BC的值，Rt△ABC中求出山高CD的值．‎ ‎【解答】解：△ABC中，∠BAC＝45°，∠ABC＝75°，∴∠ACB＝60°，‎ 由正弦定理得＝， BC＝＝1200，‎ Rt△ABC中，∠DBC＝30°，∴CD＝BCtan∠DBC＝1200×＝400，‎ 则山高CD为400m．‎ 故选：B．‎ ‎10．在正项等比数列{an}中，a2a7＝4，则log2a1+log2a2+…+log2a8＝（　　）‎ A．2 B．4 C．6 D．8‎ ‎【分析】根据对数运算法则以及等比数列性质求解．‎ ‎【解答】解：∵a2a7＝4，‎ ‎∴log2a1+log2a2+…+log2a8＝log2（a1a2…a8）＝log2＝log244＝8．‎ 故选：D．‎ ‎11．在等差数列{an}中，a8＞0，a4+a10＜0，则数列{an}的前n项和Sn中最小的是（　　）‎ A．S4 B．S5 C．S6 D．S7‎ ‎【分析】结合已知及等差数列的性质可判断出a7＜0，a8＞0，即可求解．‎ ‎【解答】解：等差数列{an}中，a8＞0，a4+a10＝2a7＜0，‎ 故a7＜0，‎ 所以数列{an}的前n项和Sn中最小的是s7．‎ 故选：D．‎ ‎12．已知{an}是公差为3的等差数列．若a1，a2，a4成等比数列，则{an}的前10项和 S10＝（　　）‎ A．165 B．138 C．60 D．30‎ ‎【分析】设公差d＝3，运用等差数列的通项公式和等比数列的中项性质，解方程可得首项，再由等差数列的求和公式，计算可得所求值．‎ ‎【解答】解：{an}是公差d为3的等差数列，若a1，a2，a4成等比数列，‎ 则a1a4＝a22，即a1（a1+9）＝（a1+3）2，解得a1＝3，‎ 又d＝3，可得S10＝10a1+×10×9d＝30+45×3＝165．‎ 故选：A．‎ ‎13． 若两个等差数列{an}，{bn}的前n项和分别为An、Bn，且满足，则的值为（　　）‎ A． B． C． D．‎ ‎【分析】利用等差数列的通项公式求和公式及其性质即可得出．‎ ‎【解答】解：＝＝×＝×＝×＝．‎ 故选：C．‎ ‎14．若数列{an}中，，则这个数列的第10项a10＝（　　）‎ A．28 B．29 C． D．‎ ‎【分析】对等式两边取倒数，结合等差数列的定义和通项公式可得an＝，计算可得a10．‎ ‎【解答】解：数列{an}中，，‎ 可得＝+3，即有＝+3（n﹣1）＝3n﹣2，则an＝，‎ 可得a10＝＝，‎ 故选：C．‎ ‎15．已知等比数列{an}的前k项和为12，前2k项和为48，则前4k项和为（　　）‎ A．324 B．480 C．108 D．156‎ ‎【分析】由等比数列的前n项和及其性质可得：Sk，S2k﹣Sk，S3k﹣S2k，S4k﹣S3k．即可得出．‎ ‎【解答】解：由等比数列的前n项和及其性质可得：（48﹣12）2＝12×（S3k﹣48），解得：S3k＝156．‎ ‎（156﹣48）2＝（48﹣12）×（S4k﹣156），解得：S4k＝480．‎ 故选：B．‎ ‎16．已知等差数列{an}的前n项和为Sn，a2＝2，S7＝28，则数列的前2020项和为（　　）‎ A． B． C． D．‎ ‎【分析】本题先根据等差数列的通项公式和求和公式可列出关于a1和d的方程组，解出a1和d的值，即可得到数列{an}的通项公式，也即求出数列的通项公式，根据通项公式的特点采用裂项相消法求出前2020项和．‎ ‎【解答】解：由题意，设等差数列{an}的公差为d，则 ‎，解得．‎ ‎∴数列{an}的通项公式为an＝1+（n﹣1）×1＝n，n∈N*．‎ ‎∴＝．‎ 设数列的前n项和为Tn，‎ 则Tn＝++…+‎ ‎＝++…+＝1﹣+﹣+…+﹣＝1﹣＝．‎ ‎∴T2020＝．‎ 故选：A．‎ ‎17．数列{an}前n项和为Sn，若2Sn＝an+1，则a7+S2019的值为（　　）‎ A．2 B．1 C．0 D．﹣1‎ ‎【分析】根据已知条件首先推知数列{an}是等比数列，首项为1，公比为﹣1．然后据此得到通项公式公式和求和公式，代入求值即可．‎ ‎【解答】解：∵2Sn＝an+1，‎ ‎∴2Sn﹣an＝1 ①‎ ‎∴当n≥2时，2Sn﹣1﹣an﹣1＝1，②‎ 由①﹣②，得2an﹣an+an﹣1＝0，化为an＝﹣an﹣1．即＝﹣1．‎ 当n＝1时，2a1﹣a1＝1，∴a1＝1．‎ ‎∴数列{an}是等比数列，首项为1，公比为﹣1．∴an＝（﹣1）n．‎ ‎∴a7+S2019＝1×（﹣1）6+＝1+1＝2，‎ 故选：A．‎ ‎18．已知数列{an}的通项，若{an}为单调递增数列，则λ的取值范围是（　　）‎ A．(﹣3，+∞） B．[﹣3，+∞） C．（﹣2，+∞） D．[﹣2，+∞）‎ ‎【解答】解：∵数列{an}的通项，λ∈R，若{an}为单调递增数列，‎ ‎∴an+1﹣an＝（n+1）2+λ（n+1）﹣2018﹣（n2+λn﹣2018）＝2n+1+λ＞0对任意的自然数n都成立，即λ＞﹣2n﹣1 恒成立，∴λ＞﹣3，‎ 故选：A．‎ ‎19．对于任意实数x，不等式ax2+2ax﹣（a+2）＜0恒成立，则实数a的取值范围是（　　）‎ A．﹣1≤a≤0 B．﹣1≤a＜0 C．﹣1＜a≤0 D．﹣1＜a＜0‎ ‎【分析】讨论a是否为0，不为0时，根据开口方向和判别式建立不等式组，解之即可求出所求．‎ ‎【解答】解：1°a＝0时，﹣2＜0成立 ‎2°a＜0时，△＝4a2+4a（a+2）＝8a2+8a＜0，∴8a（a+1）＜0，∴﹣1＜a＜0‎ 综上，实数a的取值范围是﹣1＜a≤0‎ 故选：C．‎ ‎20．若关于x的不等式的解集中恰有4个正整数，则实数m的取值范围为（　　）‎ A．（6，7] B．（6，7） C．[6，7） D．（6，+∞）‎ ‎【分析】不等式可化为（x﹣2）（x﹣m）＜0，讨论m≤2和m＞2时，求出不等式的解集，从而求得m的取值范围．‎ ‎【解答】解：原不等式可化为（x﹣2）（x﹣m）＜0，‎ 若m≤2，则不等式的解是m＜x＜2，不等式的解集中不可能有4个正整数，所以m＞2；‎ 所以不等式的解是2＜x＜m；‎ 所以不等式的解集中4个正整数分别是3，4，5，6；则m的取值范围是（6，7]．‎ 故选：A．‎ ‎21．函数的最小值是（　　）‎ A．2 B．4 C．6 D．8‎ ‎【分析】y＝2x+＝2（x﹣1）++2，然后结合基本不等式即可求解．‎ ‎【解答】解：因为y＝2x+（x＞1），＝2（x﹣1）++2＝6，‎ 当且仅当2（x﹣1）＝即x＝2时取等号，此时取得最小值6．‎ 故选：C．‎ ‎22．两个正实数a，b满足3a+b＝1，则满足恒成立的m取值范围（　　）‎ A．[﹣4，3] B．[﹣3，4] C．[﹣2，6] D．[﹣6，2]‎ ‎【分析】由基本不等式和“1”的代换，可得+的最小值，再由不等式恒成立思想可得m2﹣m小于等于最小值，解不等式可得所求范围．‎ ‎【解答】解：由3a+b＝1，a＞0，b＞0，‎ 可得+＝（3a+b）（+）＝6++≥6+2＝12，‎ 当且仅当a＝，b＝上式取得等号，‎ 由题意可得m2﹣m≤+的最小值，‎ 即有m2﹣m≤12，解得﹣3≤m≤4．‎ 故选：B．‎ ‎23．在△ABC中，角A，B，C所对的边分别为a，b，c满足b2+c2﹣a2＝bc，a＝，则b+c的取值范围是（　　）‎ A． B． C． D．‎ ‎【分析】由余弦定理可求cosA的值，结合A的范围可求A的值，由正弦定理可得：＝＝＝2，于是b+c＝2sinB+2sinC＝2sinB+2sin（﹣B）＝2sin（B+），根据已知可求B+的范围，再利用三角函数的值域即可得出．‎ ‎【解答】解：∵b2+c2﹣a2＝bc，∴cosA＝＝＝，‎ ‎∴由A∈（0，π），可得A＝，‎ ‎∵由正弦定理可得：＝＝＝2，‎ ‎∴b+c＝2sinB+2sinC＝2sinB+2sin（﹣B）＝2sinB+2（cosB+sinB）‎ ‎＝3sinB+cosB＝2sin（B+），‎ ‎∵B+C＝，∴B∈（0，），可得：B+∈（，），‎ ‎∴sin（B+）∈（，1]，∴b+c＝2sin（B+）∈（，2]，‎ 故选：B．‎ ‎24．已知数列{an}的前n项和，设，Tn为数列{bn}的前n项和，若对任意的n∈N*，不等式λTn＜9n+3恒成立，则实数λ的取值范围为（　　）‎ A．（﹣∞，48） B．（﹣∞，36） C．（﹣∞，16） D．（16，+∞）‎ ‎【解答】解：由题意，当n＝1时，a1＝S1＝•12﹣•1＝1．‎ 当n≥2时， an＝Sn﹣Sn﹣1＝n2﹣n﹣[（n﹣1）2﹣（n﹣1）]＝3n﹣2，‎ ‎∴an＝3n﹣2，n∈N*．‎ 则＝＝（﹣）．‎ 设数列{bn}的前n项和Tn，则 Tn＝b1+b2+…+bn＝（1﹣）+（﹣）+…+（﹣）‎ ‎＝（1﹣+﹣+…+﹣）＝（1﹣）＝．‎ ‎∵对任意的n∈N*，不等式λTn＜9n+3恒成立，∴对任意的n∈N*，不等式λ•＜9n+3恒成立，即对任意的n∈N*，不等式λ＜恒成立．‎ 构造数列{cn}：令cn＝，n∈N*．‎ ‎∵cn+1﹣cn＝﹣＝＞0，n∈N*．‎ ‎∴数列{cn}是单调递增数列．∴数列{cn}的最小值为c1＝48．∴λ＜48．‎ 故选：A．‎ 二．解答题（共3小题，每题10分，共30分）‎ ‎25．已知在△ABC中，角A、B、C对应的边分别为a、b、c，bsinB+asinC＝asinA+csinC．‎ ‎（1）求角B；‎ ‎（2）若c＝1，△ABC的面积为，求C．‎ ‎【分析】（1）根据正弦定理以及余弦定理建立方程进行求解即可．‎ ‎（2）根据三角形的面积公式进行计算即可．‎ ‎【解答】解：（1）由bsinB+asinC＝asinA+csinC及正弦定理 可得b2+ac＝a2+c2，‎ 由余弦定理可得，‎ 又因为B∈（0，π），所以．‎ ‎（2）因为，所以a＝1．‎ 又因为，‎ 所以△ABC是等边三角形，‎ 所以．‎ ‎26．设函数f（x）＝x2+mx+n，已知不等式f（x）＜0的解集为{x|1＜x＜4}．‎ ‎（1）求m和n的值；‎ ‎（2）若对任意x＞0恒成立，求a的取值范围．‎ ‎【分析】（1）根据一元二次不等式的解集的分界点为对应方程的根，结合韦达定理即可得到m，n的值；‎ ‎（2）因为x＞0，分离参数，转化为a≤g（x），转化为求g（x）的在（0，+∞）上的最小值．‎ ‎【解答】解：（1）依题意，1，4为方程x2+mx+n＝0的两根，‎ 所以﹣m＝1+4，n＝1×4，‎ 即m＝﹣5，n＝4；‎ ‎（2）由（1）知，f（x）＝x2﹣5x+4，‎ 所以f（x）≥ax对任意x＞0恒成立，即x2﹣5x+4≥ax对任意x＞0恒成立，‎ ‎∵x＞0，‎ ‎∴a≤x+﹣5在（0，+∞）上恒成立，‎ 当x＞0时，＞0，‎ ‎∴根据基本不等式，x+﹣5≥2﹣5＝﹣1，当且仅当x＝2时，等号成立，‎ 所以a≤﹣1．‎ ‎27．已知等差数列{an}的前n项和为Sn，且满足a4+a6＝18，S11＝121．‎ ‎（1）求数列{an}的通项公式；‎ ‎（2）设bn＝（an+3）2n，数列{bn}的前n项和为Tn，求Tn．‎ ‎【分析】（1）设数列{an}的公差为d，运用等差数列的通项公式和求和公式，解方程可得首项和公差，进而得到所求通项公式；‎ ‎（2）求得bn＝（n+1）•2n+1，运用数列的错位相减法求和，结合等比数列的求和公式，化简可得所求和．‎ ‎【解答】解：（1）设数列{an}的公差为d，a4+a6＝18，可得2a1+8d＝18，即a1+4d＝9，‎ S11＝121，可得11a1+×11×10d＝121，即a1+5d＝11，‎ 解得a1＝1，d＝2，‎ 可得an＝1+2（n﹣1）＝2n﹣1；‎ ‎（2）由（1）可知bn＝（an+3）2n＝（n+1）•2n+1，‎ 数列{bn}的前n项和为Tn＝2•22+3•23+…+（n+1）•2n+1，‎ ‎2Tn＝2•23+3•24+…+（n+1）•2n+2，‎ 两式作差，得﹣Tn＝8+23+24+…+2n+1﹣（n+1）•2n+2‎ ‎＝8+﹣（n+1）•2n+2，‎ 化简可得Tn＝n•2n+2．‎