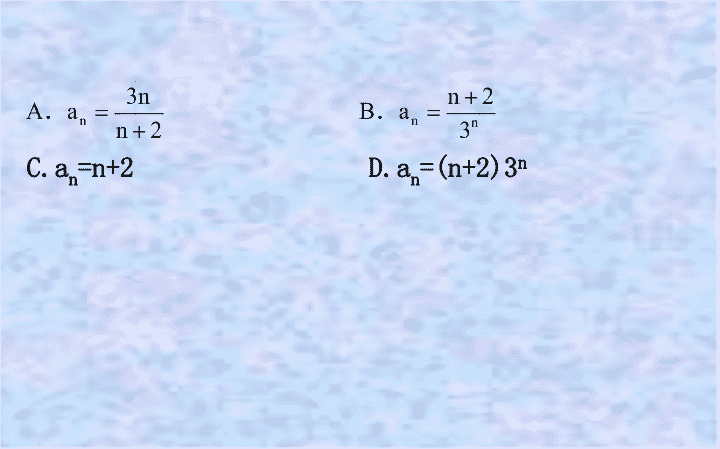2020届高考理科数学二轮专题复习课件：专题3 数列2-3-高考小题 2 54页

第 2 课时　 数列的简单问题 考向一　由递推关系求通项 ( 压轴题型考点 ) 【典例】 1. 已知数列 {a n } 满足 a 1 =1, 且 则数列 {a n } 的通项公式为 ( 　　 ) C.a n =n+2 D.a n =(n+2)3 n 【解析】 选 B. 由 a n = a n-1 + (n≥2 且 n∈N * ) 得 ,3 n a n = 3 n-1 a n-1 +1,3 n-1 a n-1 =3 n-2 a n-2 +1,…,3 2 a 2 =3a 1 +1, 以上各式 相加得 3 n a n =n+2, 故 a n = . 2.(2019· 天津一模 ) 已知数列 {a n } 满足 :a 1 = , , 则数列 {a n } 的通项公式为 a n = ( 　　 ) 【解析】 选 C. 通解 :a n+1 -1= = (a n -1), 令 b n =a n -1, 则 从而得到 , 又 b 1 =a 1 -1=- , 得 b n = b 1 , 所以 a n = . 优解 :a 1 = =1- ,a 2 = =1- ,a 3 = =1- , …, 归纳可得 a n =1- . 3. 数列 {a n } 中 ,a n >0, 前 n 项和为 S n , 且 , 则数列 {a n } 的通项公式为 ________.   【解析】 由 S n = ,a n >0,(n∈N * ) 得 a 1 = , 解得 a 1 =1, 又 S n-1 = (n≥2), 两式相减得 2a n = + a n -a n-1 , 化简得 (a n +a n-1 )(a n -a n-1 -1)=0, 因为 a n +a n-1 ≠0, 则 a n -a n-1 =1(n≥2), 则数列 {a n } 是首项和公差都等于 1 的等差数列 , 则 a n =n. 答案 : a n =n 【题眼直击】 题目 题眼 思维导引 1. ① 相邻两项成同一倍数关系 , 想到用叠加法求数列的通项 . 2. ② 相邻两项的倍数关系与 n 有关 , 想到用叠乘法求数列的通项 . 3. ③ 已知 a n 与 S n 的关系 , 想到利用通项 a n 与前 n 项和 S n 之间的关系求解 . 【拓展提升】 求数列通项常用的方法 (1) 定义法 :① 形如 a n+1 =a n +C(C 为常数 ), 直接利用定义判断其为等差数列 . ② 形如 a n+1 =ka n (k 为非零常数 ) 且首项不为零 , 直接利用定义判断其为等比数列 . (2) 叠加法 : 形如 a n+1 =a n +f(n), 利用 a n =a 1 +(a 2 -a 1 )+(a 3 - a 2 )+…+(a n -a n-1 ), 求其通项公式 . (3) 叠乘法 : 形如 =f(n)≠0, 利用 a n =a 1 · , 求其通项公式 . (4) 待定系数法 : 形如 a n+1 =pa n +q( 其中 p,q 均为常数 , pq(p-1)≠0), 先用待定系数法把原递推公式转化为 a n+1 -t=p(a n -t), 其中 t= , 再转化为等比数列求解 . (5) 构造法 : 形如 a n+1 =pa n +q n ( 其中 p,q 均为常数 ,pq(p- 1)≠0), 先在原递推公式两边同除以 q n+1 , 得 , 构造新数列 {b n } , 得 b n+1 = ·b n + , 接下来 用待定系数法求解 . 【变式训练】 1. 数列 {a n } 满足 a 1 =2,a n+1 = a n ,n∈N * , 则 a n =___.  【解析】 由已知 所以由 a 1 =2,a n = =(n+1)2 n-1 . 答案 : (n+1)2 n-1 2. 已知数列 {a n } 中 ,a 1 =3, 且点 P n (a n ,a n+1 )(n∈N * ) 在直线 4x-y+1=0 上 , 则数列 {a n } 的通项公式为 ________.  【解析】 点 P n (a n ,a n+1 )(n∈N * ) 在直线 4x-y+1=0 上 , 有 4a n -a n+1 +1=0. 即 a n+1 =4a n +1, 得 a n+1 + . 所以 是公比为 4, 首项为 a 1 + 的等比数列 . a n + ·4 n-1 , 故有 a n = ·4 n-1 - 答案 : a n = ·4 n-1 - 【补偿训练】 　　 已知在数列 {a n } 中 ,a n+1 = a n (n∈N * ), 且 a 1 =4, 则数列 {a n } 的通项公式 a n =________.  【解析】 由 a n+1 = a n , 得 两边分别相乘 , 得 , 由 a 1 =4, 得 a n = . 答案 : 考向二　数列求和 ( 压轴题型考点 ) 【典例】 1.(2019· 洛阳一模 ) 已知 S n 是非零数列 {a n } 的前 n 项的 和 , 且 S n =2a n -1 ① , 则 S 2 020 等于 ( 　　 ) A.1-2 2 019 B.2 2 020 -1 C.2 2 019 -1 D.1-2 2 020 【解析】 选 B. 因为 S n =2a n -1, 所以 S 1 =1, 且 S n =2(S n - S n-1 )-1, 即 S n =2S n-1 +1, 得 S n +1=2(S n-1 +1), 由此可得数列 {S n +1} 是首项为 2, 公比为 2 的等比数列 , 得 S n +1=2 n , 即 S n =2 n -1, 所以 S 2 020 =2 2 020 -1. 2. 已知函数 则 a 1 +a 2 +a 3 +…+a 100 = ( 　　 ) A.0 B.100 C.-100 D.10 200 【解析】 选 B. 由题意 ,a 1 +a 2 +a 3 +…+a 100 =1 2 - 2 2 -2 2 +3 2 +3 2 -4 2 -4 2 +5 2 +…+99 2 -100 2 -100 2 +101 2 = -(1+2)+(3+2)-…-(99+100)+(101+100)= -(1+2+…+99+100)+(2+3+…+100+101)=-1+101=100. 3. 已知 S n 为数列 {a n } 的前 n 项和 , 且 a 1 =1, , 则 S 2 021 =________.  【解析】 由 a n a n+1 =3 n , 得 a n-1 a n =3 n-1 (n≥2), 所以 =3(n≥2), 则数列 {a n } 的所有奇数项和偶数项均构成以 3 为公比的 等比数列 , 又 a 1 =1,a 1 a 2 =3, 所以 a 2 =3, 所以 S 2 021 = 3 1 011 -2. 答案 : 3 1 011 -2 【题眼直击】 题目 题眼 思维导引 1. ① a n 与 S n 的关系式 , 想到分析出数列模型 , 运用求和公式求解 2. ② 奇数项与偶数项的表达式不同 , 想到分组转化求和 3. ③ 相邻两项的关系与 n 有关 , 想到构造新数列求和 【拓展提升】 分类讨论思想在数列求和中的应用 (1) 当数列通项中含有 (-1) n 时 , 在求和时要注意分 n 为奇 数与偶数处理 . (2) 对已知数列满足 =q, 在求 {a n } 的前 n 项和时分奇数 项和偶数项分别求和 . 【变式训练】 1. 数列 {a n } 的前 n 项和为 S n ,a 1 =2,S n = a n+1 ,b n = log 2 a n , 则数列 的前 n 项和 T n =________.  【解析】 a 1 =2,S n = a n+1 ,n≥2 时 , S n-1 = a n , 两式作差 , 得 a n = a n+1 - a n , 化简得 =2, 检验 : 当 n=1 时 ,S 1 =a 1 = a 2 , 即 a 2 =4, =2, 所以数列 {a n } 是以 2 为首项 ,2 为公比的等比数列 ; a n =2 n ,b n =log 2 a n =n, , 前 n 项和 T n = 答案 : 2. 若数列 {a n } 的各项均为正数 , 前 n 项和为 S n , 且 a 1 =1, S n+1 +S n = (n∈N * ), 则 a 25 =________.  【解析】 因为 S n+1 +S n = (n∈N * ), 所以 S n +S n-1 = (n≥2), 所以 S n+1 +S n -S n -S n-1 = , 所以 a n+1 +a n = , 所以 a n+1 - , 所以 a 2 - =-2, 解得 a 2 = -1,a 2 =-1- ( 舍去 ), 所以 a 3 - , 解得 a 3 = ,a 3 = ( 舍去 ), a 4 - 解得 a 4 = ,a 4 =- ( 舍去 ), 于是可以猜 想 ,a 25 = . 答案 : 考向三　数列与其他知识的综合问题 ( 压轴题型考点 ) 【典例】 1. 设曲线 y=2 020x n+1 (n∈N * ) 在点 (1,2 020) 处的切线 ① 与 x 轴的交点的横坐标为 x n , 令 a n =log 2 020 x n , 则 a 1 +a 2 +…+a 2 019 的值为 ( 　　 ) A.2 020 B.2 019 C.1 D.-1 【解析】 选 D. 因为 y′=2 020(n+1)x n , 所以切线方程是 y-2 020=2 020(n+1)(x-1), 所以 x n = , 所以 a 1 +a 2 +…+a 2 019 =log 2 020 (x 1 ·x 2 ·…·x 2 019 )= log 2 020 =log 2 020 =-1. 2.(2019· 潍坊二模 ) 已知函数 f(n)=n 2 cos(nπ) ② , 且 a n =f(n), 则 a 1 +a 2 +…+a 100 = ( 　　 ) A.0 B.100 C.5 050 D.10 200 【解析】 选 C.a 1 +a 2 +a 3 +…+a 100 =-1 2 +2 2 -3 2 +4 2 -…-99 2 + 100 2 =(2 2 -1 2 )+(4 2 -3 2 )+…+(100 2 -99 2 )=3+7+…+199= =5 050. 3. 在数列 {a n } 中 ,a 1 + =2 n -1(n∈N * ), 且 a 1 = 1, 若存在 n∈N * 使得 a n ≤n(n+1)λ 成立 ③ , 则实数 λ 的最 小值为 ________.  【解析】 方法一 : 依题意得 , 数列 的前 n 项和为 2 n -1, 当 n≥2 时 , =(2 n -1)-(2 n-1 -1)=2 n-1 , 且 =2 1 -1=1=2 1-1 , 因此 =2 n-1 (n∈N * ), . 记 b n = , 则 b n >0, =1,b n+1 >b n , 数列 {b n } 是递增数列 , 数列 {b n } 的最小项是 b 1 = . 依题意得 , 存在 n∈N * 使得 λ≥ =b n 成立 , 即有 λ≥b 1 = , λ 的最小值是 . 方法二 : 由方法一知 a n =n·2 n-1 , 因为 a n ≤n(n+1)λ, 所以 n·2 n-1 ≤n(n+1)λ, 所以 λ≥ , 由方法一知 , 当 n=1 时 , 有最小值 , 所以 λ≥ , 所以 λ 最小值为 . 答案 : 【题眼直击】 题目 题眼 思维导引 1. ① 由曲线的切点想到导数的几何意义 2. ② 正负相间想到并项求和 3. ③ 分离参数求不等式恒成立问题 【拓展提升】 数列与不等式的交汇多为不等式恒成立与证明和形式的不等式 , 在求解时要注意等价转化即分离参数法与放缩法的技巧应用 . 【变式训练】 1. 已知等差数列 {a n } 的前 n 项和为 S n ,a 1 =-9,a 2 +a 3 =-12, 则使 S n 取得最小值时 n 的值为 ( 　　 ) A.2 B.4 C.5 D.7 【解析】 选 C. 因为 a 2 +a 3 =2a 1 +3d=-18+3d=-12, 解得 d=2, 从而有 S n =-9n+ ×2=n 2 -10n=(n-5) 2 - 25, 所以当 n=5 时 ,S n 最小 . 2. 已知数列 {a n } 满足 1+log 3 a n =log 3 a n+1 (n∈N * ),a 2 +a 4 + a 6 =9, 则 (a 5 +a 7 +a 9 )= ( 　　 ) A.- B. C.-5 D.5 【解析】 选 C. 由 1+log 3 a n =log 3 a n+1 (n∈N * ) 得 a n+1 =3a n (n ∈N * ), 所以数列 {a n } 为等比数列 , 且公比为 3, 因此由 a 2 +a 4 +a 6 =9 得 a 5 +a 7 +a 9 =(a 2 +a 4 +a 6 )×q 3 =9×3 3 =3 5 , 所以 (a 5 +a 7 +a 9 )= 3 5 =-5. 3. 已知数列 {a n } 的前 n 项和 S n =2a n -2 n+1 , 若不等式 2n 2 -n-3<(5-λ)a n 对 ∀n∈N * 恒成立 , 则整数 λ 的最大值为 ________.  【解析】 当 n=1 时 ,a 1 =S 1 =2a 1 -2 2 , 解得 a 1 =4, 当 n≥2 时 , S n-1 =2a n-1 -2 n , 则 a n =S n -S n-1 =2a n -2a n-1 -2 n , 得 a n =2a n-1 +2 n , 所以 所以数列 是以 2 为首项 ,1 为公差的等差数列 , =n+ 1, 即 a n =(n+1)·2 n . 因为 a n >0, 所以不等式 2n 2 -n-3<(5- λ)a n , 等价于 5-λ> . 记 b n = , 当 n≥2 时 , , 所以当 n≥3 时 , <1,(b n ) max =b 3 = , 所以 5-λ> ,λ<5- = , 所以整数 λ 的最大值为 4. 答案 : 4