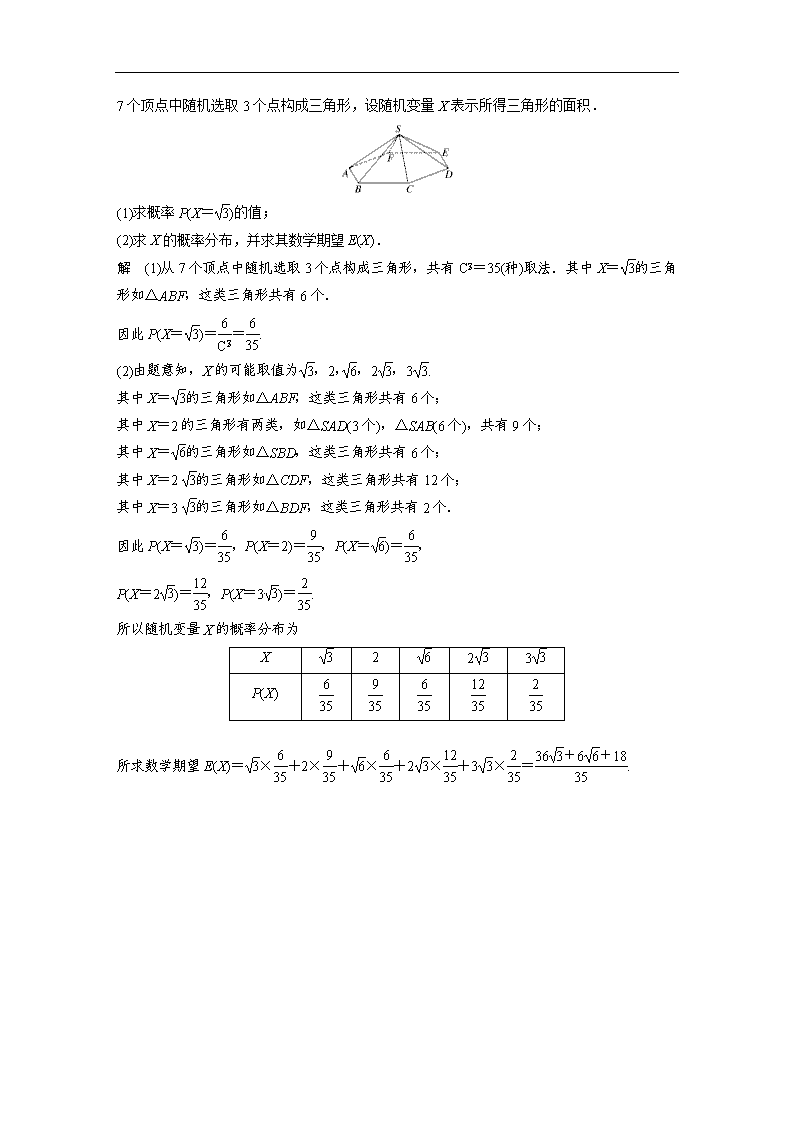2019年高考数学练习题汇总(八)随机变量及其概率分布 3页

‎(八)随机变量及其概率分布 ‎1．袋中装有大小相同的黑球和白球共9个，从中任取2个都是白球的概率为.现甲、乙两人从袋中轮流摸球，甲先取，乙后取，然后甲再取，…，每次摸取1个球，取出的球不放回，直到其中有一人取到白球时终止．用X表示取球终止时取球的总次数．‎ ‎(1)求袋中原有白球的个数；‎ ‎(2)求随机变量X的概率分布及数学期望E(X)．‎ 解　(1)设袋中原有n个白球，则从9个球中任取2个球都是白球的概率为，‎ 由题意知＝，化简得n2－n－30＝0，‎ 解得n＝6或n＝－5(舍去)，故袋中原有白球的个数为6.‎ ‎(2)由题意，X的可能取值为1,2,3,4.‎ P(X＝1)＝＝，P(X＝2)＝＝，‎ P(X＝3)＝＝，P(X＝4)＝＝.‎ 所以取球次数X的概率分布为 X ‎1‎ ‎2‎ ‎3‎ ‎4‎ P 所求数学期望E(X)＝1×＋2×＋3×＋4×＝.‎ ‎2．某射击小组有甲、乙两名射手，甲的命中率为P1＝，乙的命中率为P2，在射击比武活动中每人射击两发子弹则完成一次检测．在一次检测中，若两人命中次数相等且都不少于一发，则称该射击小组为“先进和谐组”．‎ ‎(1)若P2＝，求该小组在一次检测中荣获“先进和谐组”的概率；‎ ‎(2)在2018年每月进行1次检测，设这12次检测中该小组获得“先进和谐组”的次数为ξ，如果E(ξ)≥5，求P2的取值范围．‎ 解　(1)所求概率P＝＋＝.‎ ‎(2)该小组在一次检测中荣获“先进和谐组”的概率为 P＝[C·P2·(1－P2)]＋P＝P2－P.‎ 而ξ～B(12，P)，所以E(ξ)＝12P，‎ 由E(ξ)≥5知，·12≥5，‎ 解得≤P2≤.‎ 又0≤P2≤1，∴≤P2≤1.‎ ‎3．(2018·南通调研)从集合{1,2,3,4,5}的所有非空子集中，等可能地取出m个．‎ ‎(1)若m＝1，求所取子集的元素既有奇数又有偶数的概率；‎ ‎(2)若m＝2，记所取子集的元素个数之差的绝对值为ξ，求ξ的概率分布及数学期望E(ξ)．‎ 解　(1)当m＝1时，记事件A：“所取子集的元素既有奇数又有偶数”．‎ 则集合{1,2,3,4,5}的非空子集数为25－1＝31，其中非空子集的元素全为奇数的子集数为23－1＝7，全为偶数的子集数为22－1＝3，‎ 所以P(A)＝＝.‎ ‎(2)当m＝2时，ξ的所有可能取值为0,1,2,3,4，‎ 则P(ξ＝0)＝＝＝，‎ P(ξ＝1)＝＝＝，‎ P(ξ＝2)＝＝＝，‎ P(ξ＝3)＝＝＝，‎ P(ξ＝4)＝＝＝，‎ 所以ξ的概率分布为 ξ ‎0‎ ‎1‎ ‎2‎ ‎3‎ ‎4‎ P 所以ξ的数学期望 E(ξ)＝0×＋1×＋2×＋3×＋4×＝.‎ ‎4．(2018·启东模拟)如图，已知正六棱锥S－ABCDEF的底面边长为2，高为1.现从该棱锥的7个顶点中随机选取3个点构成三角形，设随机变量X表示所得三角形的面积．‎ ‎(1)求概率P(X＝)的值；‎ ‎(2)求X的概率分布，并求其数学期望E(X)．‎ 解　(1)从7个顶点中随机选取3个点构成三角形，共有C＝35(种)取法．其中X＝的三角形如△ABF，这类三角形共有6个．‎ 因此P(X＝)＝＝.‎ ‎(2)由题意知，X的可能取值为，2，，2，3.‎ 其中X＝的三角形如△ABF，这类三角形共有6个；‎ 其中X＝2的三角形有两类，如△SAD(3个)，△SAB(6个)，共有9个；‎ 其中X＝的三角形如△SBD，这类三角形共有6个；‎ 其中X＝2的三角形如△CDF，这类三角形共有12个；‎ 其中X＝3的三角形如△BDF，这类三角形共有2个．‎ 因此P(X＝)＝，P(X＝2)＝，P(X＝)＝，‎ P(X＝2)＝，P(X＝3)＝.‎ 所以随机变量X的概率分布为 X ‎2‎ ‎2 ‎3 P(X)‎ 所求数学期望E(X)＝×＋2×＋×＋2×＋3×＝.‎