高中数学（人教版必修5）配套练习：1-2应用举例第1课时 8页

第一章 1.2 第 1 课时 一、选择题 1．某次测量中，A 在 B 的北偏东 55°，则 B 在 A 的( ) A．北偏西 35° B．北偏东 55° C．南偏西 35° D．南偏西 55° [答案] D [解析] 根据题意和方向角的概念画出草图，如图所示．α＝55°，则β＝α＝55°.所以 B 在 A 的南偏西 55°.故应选 D． 2．两座灯塔 A 和 B 与海洋观察站 C 的距离都等于 a km，灯塔 A 在观察站 C 的北偏东 20°， 灯塔 B 在观察站 C 的南偏东 40°，则灯塔 A 与灯塔 B 的距离为( ) A．a km B． 3a km C． 2a km D．2a km [答案] B [解析] ∠ACB＝120°，AC＝BC＝a，由余弦定理可得 AB＝ 3a(km)． 3．一船向正北航行，看见正西方向有相距 10n mlie 的两个灯塔恰好与它在一条直线上， 继续航行半小时后，看见一灯塔在船的南偏西 60°方向上，另一灯塔在船的南偏西 75°方向上， 则这艘船的速度是每小时( ) A．5n mlie B．5 3n mlie C．10n mlie D．10 3n mlie [答案] C [解析] 如图，依题意有∠BAC＝60°，∠BAD＝75°， ∴∠CAD＝∠CDA＝15°，从而 CD＝CA＝10， 在 Rt△ABC 中，求得 AB＝5， ∴这艘船的速度是 5 0.5 ＝10(n mlie/h)． 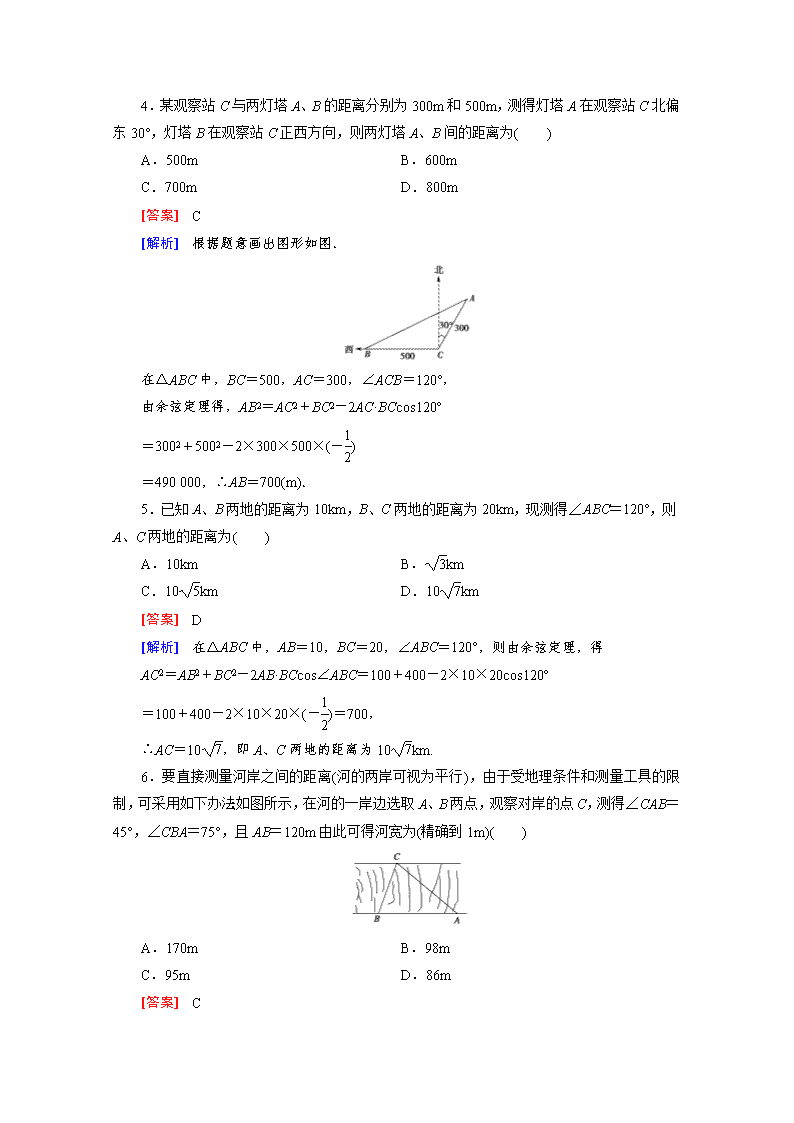4．某观察站 C 与两灯塔 A、B 的距离分别为 300m 和 500m，测得灯塔 A 在观察站 C 北偏 东 30°，灯塔 B 在观察站 C 正西方向，则两灯塔 A、B 间的距离为( ) A．500m B．600m C．700m D．800m [答案] C [解析] 根据题意画出图形如图． 在△ABC 中，BC＝500，AC＝300，∠ACB＝120°， 由余弦定理得，AB2＝AC2＋BC2－2AC·BCcos120° ＝3002＋5002－2×300×500×(－1 2) ＝490 000，∴AB＝700(m)． 5．已知 A、B 两地的距离为 10km，B、C 两地的距离为 20km，现测得∠ABC＝120°，则 A、C 两地的距离为( ) A．10km B． 3km C．10 5km D．10 7km [答案] D [解析] 在△ABC 中，AB＝10，BC＝20，∠ABC＝120°，则由余弦定理，得 AC2＝AB2＋BC2－2AB·BCcos∠ABC＝100＋400－2×10×20cos120° ＝100＋400－2×10×20×(－1 2)＝700， ∴AC＝10 7，即 A、C 两地的距离为 10 7km. 6．要直接测量河岸之间的距离(河的两岸可视为平行)，由于受地理条件和测量工具的限 制，可采用如下办法：如图所示，在河的一岸边选取 A、B 两点，观察对岸的点 C，测得∠CAB ＝45°，∠CBA＝75°，且 AB＝120m 由此可得河宽为(精确到 1m)( ) A．170m B．98m C．95m D．86m [答案] C [解析] 在△ABC 中，AB＝120，∠CAB＝45°，∠CBA＝75°，则∠ACB＝60°，由正弦定 理，得 BC＝120sin45° sin60° ＝40 6. 设△ABC 中，AB 边上的高为 h，则 h 即为河宽， ∴h＝BC·sin∠CBA＝40 6×sin75°≈95(m) 二、填空题 7．如图所示，为了测量河的宽度 BC，最适宜测量的两个数据是________． [答案] AC 与∠A． [解析] 由图可知，AB 与 BC 不能直接测量． 8．一船以 24 km/h 的速度向正北方向航行，在点 A 处望见灯塔 S 在船的北偏东 30°方向 上，15 min 后到点 B 处望见灯塔在船的北偏东 65°方向上，则船在点 B 时与灯塔 S 的距离是 ______ km.(精确到 0.1 km) [答案] 5.2 [解析] 作出示意图如图．由题意知， 则 AB＝24×15 60 ＝6，∠ASB＝35°，由正弦定理 6 sin35° ＝ BS sin30° ，可得 BS≈5.2(km)． 三、解答题 9．如图，我炮兵阵地位于地面 A 处，两观察所分别位于地面点 C 和 D 处，已知 CD＝6 000 m．∠ACD＝45°，∠ADC＝75°，目标出现于地面 B 处时测得∠BCD＝30°，∠BDC＝15°.求炮 兵阵地到目标的距离．(结果保留根号) [分析] 由于∠ADC＝75°，∠BDC＝15°，∴∠ADB 为直角．题中有多个三角形而抓住△ ABD 为 Rt△作为突破口可简化计算． [解析] 在△ACD 中，∠CAD＝60°，AD＝CD·sin45° sin60° ＝ 6 3 CD． 在△BCD 中，∠CBD＝135°，BD＝CD·sin30° sin135° ＝ 2 2 CD， ∠ADB＝90°. 在 Rt△ABD 中，AB＝ AD2＋BD2＝ 42 6 CD ＝1 000 42(m)． 10．一艘船以 32.2n mile/h 的速度向正北航行．在 A 处看灯塔 S 在船的北偏东 20°的方向， 30min 后航行到 B 处，在 B 处看灯塔在船的北偏东 65°的方向，已知距离此灯塔 6.5n mile 以外 的海区为航行安全区域，这艘船可以继续沿正北方向航行吗？ [解析 ] 在△ASB 中， ∠SBA＝ 115° ，∠ S＝45°. 由正弦 定理，得 SB＝ ABsin20° sin45° ＝ 16.1sin20° sin45° ≈7.787(n mile)．设点 S 到直线 AB 的距离为 h，则 h＝SBsin65°≈7.06(n mile)． ∵h>6.5n mile，∴此船可以继续沿正北方向航行. 一、选择题 1．已知船 A 在灯塔 C 北偏东 85°且到 C 的距离为 2km，船 B 在灯塔 C 西偏北 25°且到 C 的距离为 3km，则 A、B 两船的距离为( ) A．2 3km B．3 2km C． 15km D． 13km [答案] D [解析] 如图可知∠ACB＝85°＋(90°－25°)＝150°， AC＝2，BC＝ 3， ∴AB2＝AC2＋BC2－2AC·BC·cos150°＝13， ∴AB＝ 13. 2．甲船在湖中 B 岛的正南 A 处，AB＝3km，甲船以 8km/h 的速度向正北方向航行，同时 乙船从 B 岛出发，以 12km/h 的速度向北偏东 60°方向驶去，则行驶 15min 时，两船的距离是 ( ) A． 7km B． 13km C． 19km D． 10－3 3km [答案] B [解析] 由题意知 AM＝8×15 60 ＝2，BN＝12×15 60 ＝3，MB＝AB－AM＝3－2＝1，所以由余 弦定理得 MN2＝MB2＋BN2－2MB·BNcos120°＝1＋9－2×1×3×(－1 2)＝13，所以 MN＝ 13km. 3．一船自西向东匀速航行，上午 10 时到达一座灯塔 P 的南偏西 75°距塔 68n mile 的 M 处，下午 2 时到达这座灯塔的东南方向的 N 处，则这只船的航行速度为( ) A．17 6 2 n mile/h B．34 6n mile/h C．17 2 2 n mile/h D．34 2n mile/h [答案] A [解析] 如图所示，在△PMN 中， PM sin45° ＝ MN sin120° ， ∴MN＝ 68× 3 2 2 2 ＝34 6，∴v＝MN 4 ＝17 6 2 (n mile/h)． 4．如图，货轮在海上以 40 km/h 的速度沿着方位角(从指北方 向顺时针转到目标方向线的水平角)为 140°的方向航行．为了确定船 的位置，船在 B 点观测灯塔 A 的方位角为 110°，航行1 2 h 到达 C 点， 观测灯塔 A 的方位角是 65°，则货轮到达 C 点时，与灯塔 A 的距离是( ) A．10km B．10 2km C．15km D．15 2km [答案] B [解析] 在△ABC 中，BC＝40×1 2 ＝20(km)，∠ABC＝140°－110°＝30°，∠ACB＝(180°－ 140°)＋65°＝105°， 则 A＝180°－(30°＋105°)＝45°. 由正弦定理，得 AC＝BC·sin∠ABC sinA ＝20·sin30° sin45° ＝10 2(km)． 二、填空题 5．海上一观测站测得方位角 240°的方向上有一艘停止航行待修的商船，在商船的正东方 有一艘海盗船正向它靠近，速度为每小时 90n mile.此时海盗船距观测站 10 7n mile,20min 后 测得海盗船距观测站 20n mlie，再过________min，海盗船到达商船． [答案] 40 3 [解析] 如下图，设开始时观测站、商船、海盗船分别位于 A、B、C 处，20min 后，海盗 船到达 D 处，在△ADC 中，AC＝10 7，AD＝20，CD＝30，由余弦定理，得 cos∠ADC＝AD2＋CD2－AC2 2AD×CD ＝400＋900－700 2×20×30 ＝1 2. ∴∠ADC＝60°，在△ABD 中，由已知得∠ABD＝30°， ∠BAD＝60°－30°＝30°， ∴BD＝AD＝20，20 90 ×60＝40 3 (min)． 6.如图，一艘船上午 8 00 在 A 处测得灯塔 S 在它的北偏东 30°处，之后它继续沿正北方 向匀速航行，上午 8 30 到达 B 处，此时又测得灯塔 S 在它的北偏东 75°处，且与它相距 4 2n mile，则此船的航行速度是________n mile/h. [答案] 16 [解析] 在△ABS 中，∠A＝30°，∠ABS＝105°， ∴∠ASB＝45°， ∵BS＝4 2， BS sinA ＝ AB sin∠ASB ， ∴AB＝BS·sin∠ASB sinA ＝ 4 2× 2 2 1 2 ＝8， ∵上午 8 00 在 A 地，8 30 在 B 地， ∴航行 0.5 小时的路程为 8n mile， ∴此船的航速为 16n mile/h. 三、解答题 7．海上某货轮在 A 处看灯塔 B，在货轮北偏东 75°，距离为 12 6n mile；在 A 处看灯塔 C， 在货轮的北偏西 30°，距离为 8 3n mile；货轮向正北由 A 处航行到 D 处时看灯塔 B 的方位角 为 120°.求： (1)A 处与 D 处的距离； (2)灯塔 C 与 D 处之间的距离． [解析] 由题意，画出示意图，如图所示． (1)在△ABD 中，由已知∠ADB＝60°，则 B＝45°. 由正弦定理，得 AD＝ABsin45° sin60° ＝24(n mile) (2)在△ADC 中，由余弦定理，得 CD2＝AD2＋AC2－2AD×ACcos30° ＝242＋(8 3)2－2×24×8 3× 3 2 ＝(8 3)2， ∴CD＝8 3(n mile) 答：A 处与 D 处之间距离为 24n mile，灯塔 C 与 D 处之间的距离为 8 3n mile. 8．如图，为了解某海域海底构造，在海平面内一条直线上的 A、B、C 三点进行测量，已 知 AB＝50m，BC＝120m，于 A 处测得水深 AD＝80m，于 B 处测得水深 BE＝200m，于 C 处 测得水深 CF＝110m，求∠DEF 的余弦值． [解析] 由题意可得 DE2＝502＋1202＝1302， DF2＝1702＋302＝29800， EF2＝1202＋902＝1502， 由余弦定理，得 cos∠DEF＝16 65.