2020版高中数学 第一章 解三角形 第1课时 距离和高度问题 5页

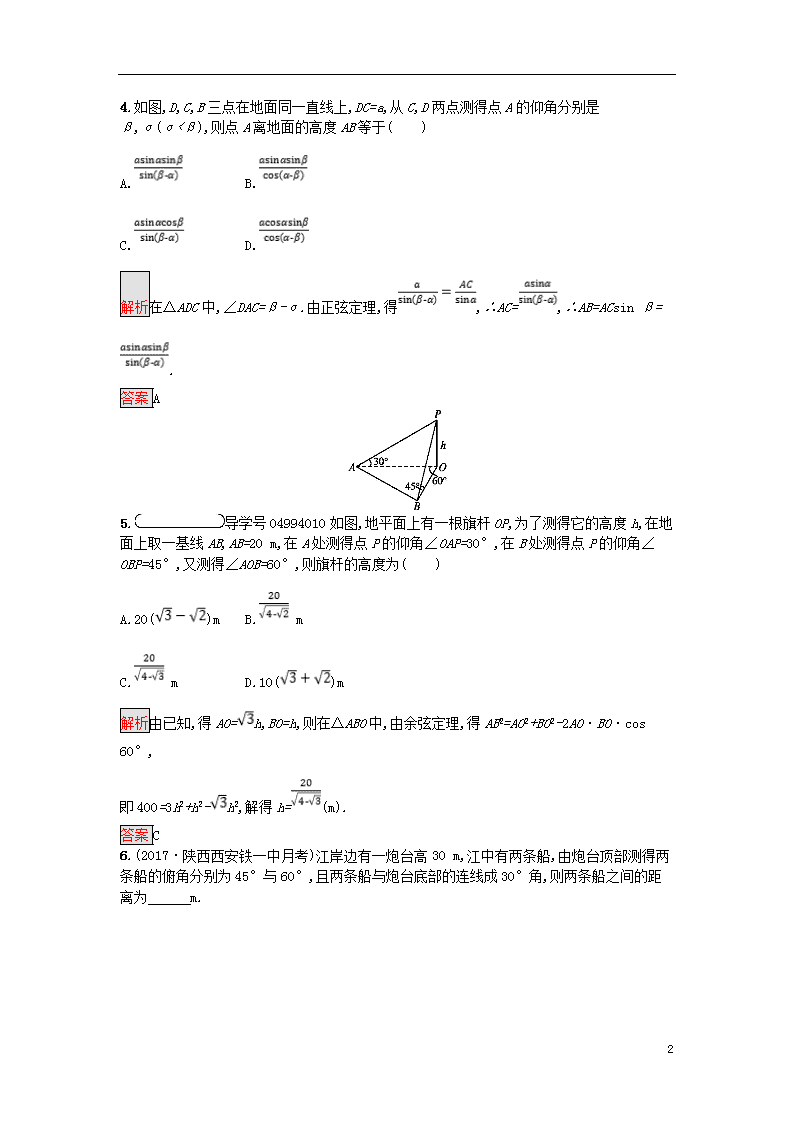
第1课时　距离和高度问题 课后篇巩固探究 ‎　　　　　　　　　　　　　　　　　‎ ‎1.(2017·河南郑州一中期中考试)如图,要测量某湖泊两侧A,B两点间的距离,若给出下列数据,则其中不能唯一确定A,B两点间的距离的是(　　)‎ A.角A,B和边b B.角A,B和边a C.边a,b和角C D.边a,b和角A 解析根据正弦定理,可知当已知两边和其中一边的对角时,解三角形得出的结果不一定唯一,故选D.‎ 答案D ‎2.如果在测量中,某渠道斜坡的坡度为,设α为坡角,那么cos α等于(　　)‎ A. B. C. D.‎ 解析由题意,知tan α=.因为0<α<,得cos α=,故选B.‎ 答案B ‎3.如图,在河岸一侧取A,B两点,在河岸另一侧取一点C,若AB=‎12 m,借助测角仪测得∠CAB=45°,∠CBA=60°,则C处河面宽CD为(　　)‎ A.6(3+)m B.6(3-)m C.6(3+2)m D.6(3-2)m 解析由⇒AB=AD+BD=CD=12⇒CD=6(3-)m,故选B.‎ 答案B 5‎ ‎4.如图,D,C,B三点在地面同一直线上,DC=a,从C,D两点测得点A的仰角分别是β,α(α<β),则点A离地面的高度AB等于(　　)‎ A. B.‎ C. D.‎ 解析在△ADC中,∠DAC=β-α.由正弦定理,得,∴AC=,∴AB=ACsin β=.‎ 答案A ‎5.导学号04994010如图,地平面上有一根旗杆OP,为了测得它的高度h,在地面上取一基线AB,AB=‎20 m,在A处测得点P的仰角∠OAP=30°,在B处测得点P的仰角∠OBP=45°,又测得∠AOB=60°,则旗杆的高度为(　　)‎ A.20()m B. m C. m D.10()m 解析由已知,得AO=h,BO=h,则在△ABO中,由余弦定理,得AB2=AO2+BO2-2AO·BO·cos 60°,‎ 即400=3h2+h2-h2,解得h=(m).‎ 答案C ‎6.(2017·陕西西安铁一中月考)江岸边有一炮台高‎30 m,江中有两条船,由炮台顶部测得两条船的俯角分别为45°与60°,且两条船与炮台底部的连线成30°角,则两条船之间的距离为　　　m. 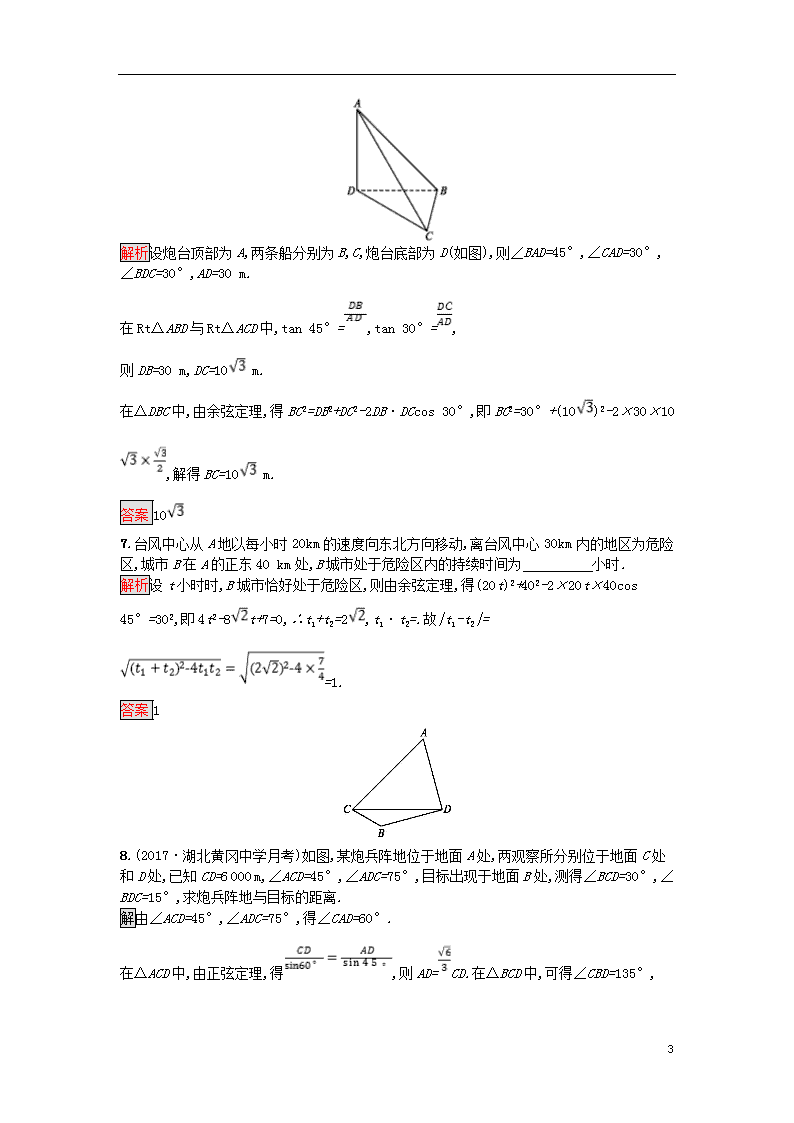‎ 5‎ 解析设炮台顶部为A,两条船分别为B,C,炮台底部为D(如图),则∠BAD=45°,∠CAD=30°,∠BDC=30°,AD=‎30 m.‎ 在Rt△ABD与Rt△ACD中,tan 45°=,tan 30°=,‎ 则DB=‎30 m,DC=‎10 m.‎ 在△DBC中,由余弦定理,得BC2=DB2+DC2-2DB·DCcos 30°,即BC2=30°+(10)2-2×30×10,解得BC=‎10 m.‎ 答案10‎ ‎7.台风中心从A地以每小时‎20 km的速度向东北方向移动,离台风中心‎30 km内的地区为危险区,城市B在A的正东‎40 km处,B城市处于危险区内的持续时间为　　　　　小时. ‎ 解析设t小时时,B城市恰好处于危险区,则由余弦定理,得(20t)2+402-2×20t×40cos 45°=302,即4t2-8t+7=0,∴t1+t2=2,t1·t2=.故|t1-t2|==1.‎ 答案1‎ ‎8.(2017·湖北黄冈中学月考)如图,某炮兵阵地位于地面A处,两观察所分别位于地面C处和D处,已知CD=6 ‎000 m,∠ACD=45°,∠ADC=75°,目标出现于地面B处,测得∠BCD=30°,∠BDC=15°,求炮兵阵地与目标的距离.‎ 解由∠ACD=45°,∠ADC=75°,得∠CAD=60°.‎ 在△ACD中,由正弦定理,得,则AD=CD.在△BCD中,可得∠CBD=135°,‎ 5‎ 由正弦定理,得BD=CD.又∠ADB=∠ADC+∠BDC=75°+15°=90°,连接AB,则在△ABD中,AD=CD=×6 000=1 000(m).‎ 故炮兵阵地与目标的距离为1 ‎000 m.‎ ‎9.导学号04994011如图,A,B,C,D都在同一个铅垂面内(与水平面垂直的平面),B,D为海岛上两座灯塔的塔顶.测量船于A处测得点B和点D的仰角分别为75°,30°,于C处测得点B和点D的仰角均为60°,AC=‎1 km,求点B,D间的距离.‎ 解(方法一)在△ACD中,∠ADC=60°-∠DAC=60°-30°=30°.由正弦定理,得AD=.‎ 在△ABC中,∠ABC=75°-60°=15°,∠ACB=60°,‎ 由正弦定理,得AB=.在△ADB中,∠BAD=180°-75°-30°=75°,由余弦定理,得BD=‎ ‎=.即点B,D间的距离为 km.‎ 5‎ ‎(方法二)如图,过点D作DH垂直于水平线于点H,过点B作BE垂直于水平线于点E,记AD与BC的交点为M.由外角定理,得∠CDA=∠DCH-∠DAC=60°-30°=30°,所以∠DAC=∠DCH-∠CDA=30°,所以AC=DC.又易知∠MCD=∠MCA=60°,‎ 所以△AMC≌△DMC,‎ 所以M为AD的中点,‎ 所以BA=BD.‎ 又AB=,‎ 所以BD=.‎ 所以点B,D间的距离为 km.‎ 5‎