A圆(基础)-教案（初中基礎，高中複習用） 6页

1 第 讲 圆（基础） 1、与圆有关的角——圆心角、圆周角 （1）图中的圆心角 ；圆周角 ① ； （2）如图，已知∠AOB=50 度，则∠ACB= ② 度； （3）在上图中，若 AB 是圆 O 的直径，则∠AOB= ③ 度； 2、圆的对称性： （1）圆是轴对称图形，其对称轴是任意一条 的直线；圆是中心对称图形，对称中心为 ④ ． （2）垂径定理：垂直于弦的直径平分这条弦，并且平分弦所对的弧． 如图，∵CD 是圆 O 的直径，CD⊥AB 于 E ∴ = ， = ⑤ 3、点和圆的位置关系有三种：点在圆 ，点在圆 ，点在圆 ⑥ ； 例 1：已知圆的半径 r 等于 5 厘米，点到圆心的距离为 d （1）当 d=2 厘米时，有 d r，点在圆 ⑦ （2）当 d=7 厘米时，有 d r，点在圆 ⑧ （3）当 d=5 厘米时，有 d r，点在圆 ⑨ 4、直线和圆的位置关系有三种：相 、相 、相 ⑩ ． 例 2：已知圆的半径 r 等于 12 厘米，圆心到直线 l 的距离为 d， （1）当 d=10 厘米时，有 d r，直线 l 与圆 ⑪ （2）当 d=12 厘米时，有 d r，直线 l 与圆 ⑫ （3）当 d=15 厘米时，有 d r，直线 l 与圆 ⑬ 5、圆与圆的位置关系：例 3：已知⊙O1 的半径为 6 厘米，⊙O2 的半径为 8 厘米，圆心距为 d，则：R+r= ， R－r= ⑭ ； （1）当 d=14 厘米时，因为 d R+r，则⊙O1 和⊙O2 位置关系是： ⑮ （2）当 d=2 厘米时， 因为 d R－r，则⊙O1 和⊙O2 位置关系是： ⑯ （3）当 d=15 厘米时，因为 ，则⊙O1 和⊙O2 位置关系是： ⑰ （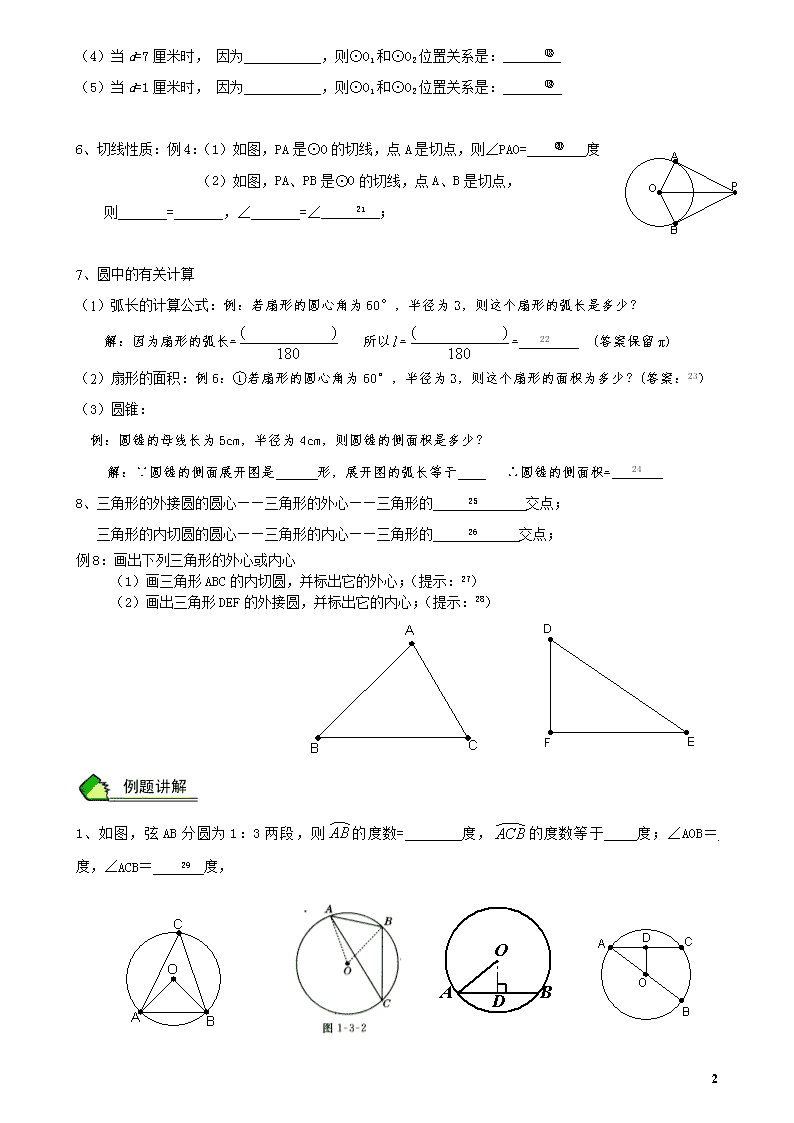4）当 d=7 厘米时， 因为 ，则⊙O1 和⊙O2 位置关系是： ⑱ O A C B E C O A B D 2 O BA C （5）当 d=1 厘米时， 因为 ，则⊙O1 和⊙O2 位置关系是： ⑲ 6、切线性质：例 4：（1）如图，PA 是⊙O 的切线，点 A 是切点，则∠PAO= ⑳ 度 （2）如图，PA、PB 是⊙O 的切线，点 A、B 是切点， 则 = ，∠ =∠ 21 ； 7、圆中的有关计算 （1）弧长的计算公式：例：若扇形的圆心角为 60°，半径为 3，则这个扇形的弧长是多少？ 解：因为扇形的弧长= ( ) 180  所以l = ( ) 180  = 22 (答案保留π) （2）扇形的面积：例 6：①若扇形的圆心角为 60°，半径为 3，则这个扇形的面积为多少？(答案：23） （3）圆锥： 例：圆锥的母线长为 5cm，半径为 4cm，则圆锥的侧面积是多少？ 解：∵圆锥的侧面展开图是 形，展开图的弧长等于 ∴圆锥的侧面积= 24 8、三角形的外接圆的圆心——三角形的外心——三角形的 25 交点； 三角形的内切圆的圆心——三角形的内心——三角形的 26 交点； 例 8：画出下列三角形的外心或内心 （1）画三角形 ABC 的内切圆，并标出它的外心；（提示：27） （2）画出三角形 DEF 的外接圆，并标出它的内心；（提示：28） 1、如图，弦 AB 分圆为 1：3 两段，则 AB 的度数= 度，ACB 的度数等于 度；∠AOB＝ 度， ∠ACB＝ 29 度， · O A BD 第 1 小题 第 3 小题 第 4、5 小题 D O CA B 第 6 小题 B C A D EF O B P A 3 2、如图，已知 A、B、C 为⊙O 上三点，若 AB 、 CA 、 BC 的度数之比 为 1∶2∶3，则∠AOB＝ ， ∠AOC＝ ， ∠ACB＝ 30 ， 相交弦： 3、如图 1－3－2，在⊙O 中，弦 AB=1.8cm，圆周角∠ACB=30○ ，则 ⊙O 的半径等于=___31___cm． 4、⊙O 的半径为 5，圆心 O 到弦 AB 的距离 OD=3，则 AD= ，AB 的长为 32 ； 5、如图，已知⊙O 的半径 OA=13 ㎝，弦 AB＝24 ㎝，则 OD= 33 ㎝。 6、如图,已知⊙O 的直径 AB＝10cm，弦 AC＝8cm, 则弦心距 OD 等于 34 cm. 圆圆关系： 7、已知：⊙O1 的半径为 3，⊙O2 的半径为 4，若⊙O1 与⊙O2 外切，则 O1O2＝ 35 。 8、已知：⊙O1 的半径为 3，⊙O2 的半径为 4，若⊙O1 与⊙O2 内切，则 O1O2＝ 36 。 9、已知：⊙O1 的半径为 3，⊙O2 的半径为 4，若⊙O1 与⊙O2 相切，则 O1O2＝ 37 。 10、已知：⊙O1 的半径为 3，⊙O2 的半径为 4，若⊙O1 与⊙O2 相交，则两圆的圆心距 d 的取值范围是 38 11、已知⊙O1 和⊙O2 外切，且圆心距为 10cm，若⊙O1 的半径为 3cm，则⊙O2 的半径为___39___cm． 12、已知⊙O1 和⊙O2 内切，且圆心距为 10cm，若⊙O1 的半径为 3cm，则⊙O2 的半径为____40___cm． 13、已知⊙O1 和⊙O2 相切，且圆心距为 10cm，若⊙O1 的半径为 3cm，则⊙O2 的半径为___41___cm． O A B C 4 O P A C B D E O C B A D O A D B C O B A P D C O B A E F O C A D B 1、已知⊙O 的半径为 5cm，A 为线段 OP 的中点，当 OP＝6cm 时，点 A 与⊙O 的位置关系是＿42＿。 A、点 A 在⊙O 内 B、点 A 在⊙O 上 C、点 A 在⊙O 外 D、不能确定 2、若圆的一条弦长为 12cm，其弦心距等于 8cm，则该圆的半径等于＿43＿cm。 3、如图，有一圆弧开桥拱，拱的跨度 AB＝16cm，拱高 CD＝4cm，那么拱形的半径是＿44＿m。 4、如图，点 P 是半径为 5 的⊙O 内一点，且 OP＝3，在过点 P 的所有的⊙O 的弦中，弦长为整数的弦的 条数为＿45＿。 A、2 B、3 C、4 D、5 5、中华人民共和国国旗上的五角星是正五角星，则五角星的每个角均是＿46＿度。 6、半径为 1 的圆中有一条弦，如果它的长为 3 ，那么这条弦所对的圆周角的度数等于＿47＿。 7、如图，四边形 ABCD 内接于⊙O，若它的一个外角∠DCE＝70°，则∠BOD 等于＿48＿。 8、如图，四边形 ABCD 内接于半⊙O，AB 是直径。 (1)请你添加一个条件，使图中的四边形 ABCD 成等腰梯形，这个条件是＿49＿＿＿(只需填一个条件)。 (2)如果 CD＝0.5AB，请你设计一个方案，将等腰梯形 ABCD 分成面积相等的三个部分。 （答案：50） 9、如图，⊙O 的直径为 10，弦 AB＝8，P 是弦 AB 上的一个动点，那么 OP 的长的取值范围是＿51＿。 10、如图，AB 是⊙O 的直径，CD 是弦，若 AB＝10cm，CD＝8cm，那么 A、B 两点到直线 CD 的距离之 和为＿52＿。 A、12cm B、10cm C、8cm D、6cm 11、如图，四边形 ABCD 为⊙O 的内接四边形，若∠ABC＝125°，则∠AOC 等于＿53＿。 A、55° B、110° C、105° D、125° 12、一条弦把圆分为 2∶3 两部分，那么这条弦所对的圆周角的度数等于＿54＿。 答案： （1） ∠AOB、∠ACB （2） 25 （3） 180 （4） 直徑所在的、圓心 5 （5） AE = BE ， 弧 AC = 弧 BC （6） 点在圆上，点在圆外，点在圆內 （7） 有 d < r，点在圆內 （8） 有 d > r，点在圆外 （9） 有 d = r，点在圆上 （10） 相離、相 切、相交 （11） 有 d < r，直线 l 与圆相交 （12） 有 d = r，直线 l 与圆相切 （13） 有 d > r，直线 l 与圆相離 （14） R+r=14， R－r=2 （15） d=R+r，外切 （16） d =R－r，內切 （17）d> R+r ，外離 （18）R－r < d < R+r，相交 （19）d < R－r，內含 （20）90 （21）PA = PB ，∠APO =∠BPO （22）π （23）  2 3 （24） 扇、 8 、20π （25）中垂線 （26）角平分線 （27）作中垂線交點 （28）作角平分線交點 （29） 90、270、90、45 （30） 60、120、30 （31） 1.8 （32） 4、 8 （33） 5 （34） 3 （35） 7 （36） 1 （37） 1 或 7 （38） 1 r，点在圆外 ⑨ 有 d = r，点在圆上 ⑩ 相離、相 切、相交 ⑪ 有 d < r，直线 l 与圆相交 ⑫ 有 d = r，直线 l 与圆相切 ⑬ 有 d > r，直线 l 与圆相離 ⑭ R+r=14， R－r=2 ⑮ d=R+r，外切 ⑯ d =R－r，內切 ⑰ d> R+r ，外離 ⑱ R－r < d < R+r，相交 ⑲ d < R－r，內含 ⑳ 90 21 PA = PB ，∠APO =∠ BPO 22 π 23  2 3 24 扇、 8 、20π 6 25 中垂線 26 角平分線 27 作中垂線交點 28 作角平分線交點 29 90、270、90、45 30 60、120、30 31 1.8 32 4、 8 33 5 34 3 35 7 36 1 37 1 或 7 38 1